Sotsiaalse Analüüsi Meetodite ja Metodoloogia õpibaas
Risttabelid ja seosekordajad
Kadri Rootalu
2014
Risttabel ehk kahemõõtmeline sagedustabel
Risttabel on kahemõõtmeline sagedustabel, kus esitatakse vastajate sagedused lähtuvalt kahest vaatluse all olevast tunnusest (vt tabel 1).
Tabel 1. Risttabel: presidendikandidaadi eelistus sõltuvalt vastaja soost
|
|
T. H. Ilves |
A. Rüütel |
Kokku |
|
Mehed |
30 |
10 |
40 |
|
Naised |
25 |
35 |
60 |
|
Kokku |
55 |
45 |
100 |
Risttabelis võivad olla esitatud vastajate arvud või osakaalud. Viimasel juhul võib eristada protsente sõltuvalt risttabeli elementidest, mille suhtes need võetud on.
Risttabeli elementideks on read, veerud ja lahtrid, mille järgi nimetatakse ka tabelisse märgitavaid protsente.
Rea protsendid näitavad, mitu protsenti selle rea inimestest kuulub ühte või teise veergu, nt tabelis 2 pooldab 75% meestest T. H. Ilvese kandidatuuri.
Tabel 2. Risttabel rea protsentidega
|
|
T. H. Ilves |
A. Rüütel |
Kokku |
|
Mehed |
75% |
25% |
100% |
|
Naised |
25% |
75% |
100% |
|
Kokku |
45% |
55% |
100% |
Veeru protsendid näitavad, mitu protsenti selle veeru inimestest kuulub ühte või teise ritta, nt tabelis 3 on T. H. Ilvese pooldajatest 55% mehed ja 45% naised.
Tabel 3. Risttabel veeru protsentidega
|
|
T. H. Ilves |
A. Rüütel |
Kokku |
|
Mehed |
55% |
22% |
40% |
|
Naised |
45% |
78% |
60% |
|
Kokku |
100% |
100% |
100 |
Üldised protsendid näitavad, mitu protsenti selle tabeli inimestest kuulub ühte või teise lahtrisse, nt tabeli 4 puhul on näha, et A. Rüütli meessoost toetajad moodustasid kogu vastajaskonnast 10%.
Tabel 4. Risttabel üldprotsentidega
|
|
T. H. Ilves |
A. Rüütel |
Kokku |
|
Mehed |
30% |
10% |
40% |
|
Naised |
25% |
35% |
60% |
|
Kokku |
55% |
45% |
100% |
Risttabeli põhjal seoste kirjeldamine on tavalugejale kindlasti kõige arusaadavam tulemuste esituse viis. Soovides aga valimiuuringu korral teha järeldusi üldkogumi kohta, tuleks kasutada lisaks risttabelile ka seosekordajaid.
Seosekordajad
Seosekordajaid kasutatakse kahe nominaal- või järjestustunnuse vahelise seose uurimiseks, kuigi nende kasutamine tuleks kõne alla ka väikese väärtuste arvuga arvtunnuste puhul. Seosekordajate leidmisel tuginetakse risttabelile. Sagedamini kasutatavateks seosekordajateks on hii-ruut-statistik ja Crameri V.
Hii-ruut-statistik
Hii-ruut-statistiku puhul vaadatakse kahe tunnuse tegelikku ühist jaotust (nt vastajate arve risttabelis) ning võrreldakse seda jaotusega (nt risttabeliga) sellises olukorras, kus kahe tunnuse vahel seost poleks. Kui nende jaotuste erinevus on suur, siis on ka hii-ruut-statistiku väärtus suur. Kui need jaotused langevad täpselt kokku, siis on hii-ruut-statistiku väärtuseks 0 (vt valemit).
Hii-ruut-statistiku maksimaalne väärtus sõltub tabeli suurusest ja vastajate arvust. Seega ei saa erineva suurusega kogumite põhjal või erineva lahtrite arvuga tabelite põhjal leitud hii-ruut-statistikuid omavahel võrrelda.
Hii-ruut-statistikut on võimalik välja arvutada levinumate statistikaprogrammidega (SPSS, STATA jms), kuid selle arvutamiseks on olemas ka netikalkulaatoreid, nt SIIN ja SIIN.
Probleemid
Hii-ruut-statistikut ei ole hea kasutada siis, kui vaadeldavatel tunnustel on palju kategooriaid (vastusevariante). Sellisel juhul on oht, et hii-ruut-statistiku aluseks olevasse tabelisse jääb tühje lahtreid, mille suhtes statistik on tundlik. Võimalusel tasuks siis kategooriaid ümber kodeerida nii, et igas oleks piisavalt palju vastajaid [viide ümberkodeerimise teemale].
Crameri V
Crameri V on hii-ruut-statistikust edasi arendatud seosekordaja, mis arvestab ka vastajate arvu ning tabeli suurust (vt valemit).
Crameri V ei saa olla kunagi suurem kui 1 ning selle minimaalseks väärtuseks on 0. Erinevate tabelite põhjal välja arvutatud Crameri V kordajad on omavahel võrreldavad: kordaja väärtusega 0,4 viitab tugevamale seosele kui kordaja väärtusega 0,3.
Avage andmestik ess12eesti.sav
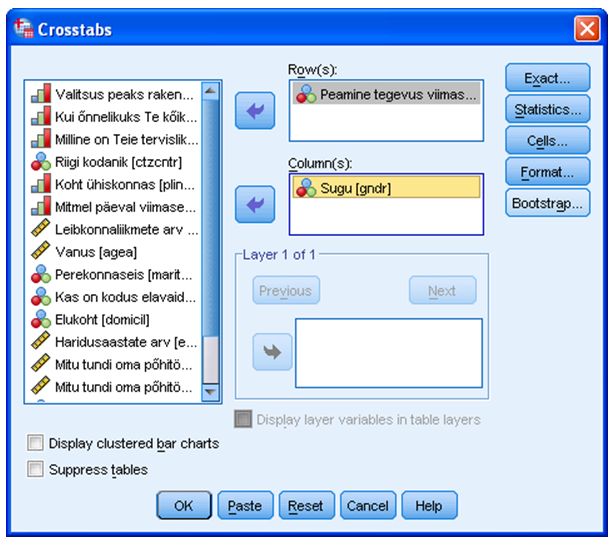
Risttabelid ehk mitmemõõtmelised sagedustabelid on paketi SPSS puhul tellitavad kirjeldava statistika alammenüüst (vt joonis 1)
Analyze – Descriptive Statistics – Crosstabs
Joonis 1. Risttabelite ja seosekordajate tellimine
Järgnevas tellimisaknas (joonis 2) saab tunnuseid saata järgmistesse akendesse:
„Row(s)“: reatunnus
„Column(s)“: veerutunnus
„Layer“: kihitunnus (eraldi tabelid)
Praeguses näites soovime vaadata vastajate peamist tegevusala nende soo lõikes. Seetõttu saadame reatunnuseks „Peamine tegevus …“ ning veerutunnuseks „Sugu“. Nupu alla „Layer“ tunnuseid lisades saaks tellida ka kolme- ja rohkemamõõtmelisi tabeleid.
Joonis 2. Risttabelite tellimise aken
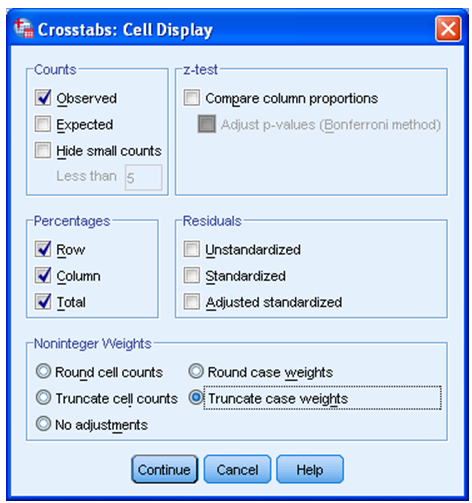
Nupu alt „Cells“ saab määrata tabeli lahtrites näidatavat infot (vastajate arvud, protsendid jne, vt joonis 3).
Praeguses näites (joonis 3) valime vastajate arvu („Observed“) ning rea, veeru ja üldprotsendid („Percentage“ alt).
Reaprotsent („Row“): mitu protsenti selle rea inimestest kuulub ühte või teise veergu.
Veeruprotsent („Column“): mitu protsenti selle veeru inimestest kuulub ühte või teise ritta.
Üldprotsendid („Total“): mitu protsenti selle tabeli inimestest kuulub ühte või teise lahtrisse. Protsendi valik sõltub uurimisülesandest, tavaliselt pole tabelisse vaja rohkem kui ühte liiki protsenti.
Joonis 3. Risttabeli tellimise aken lahtrisisese info määramiseks
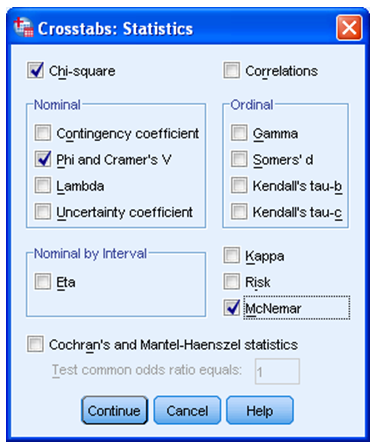
Nupu „Statistics“ alt (joonis 2) saab valida seosekordajaid.
Praeguses näites (joonis 4) valime hii-ruut-statistiku „Chi-square“ ja Crameri V saamiseks „Phi and Cramer’s V“
Joonis 4. Seosekordajate valimine
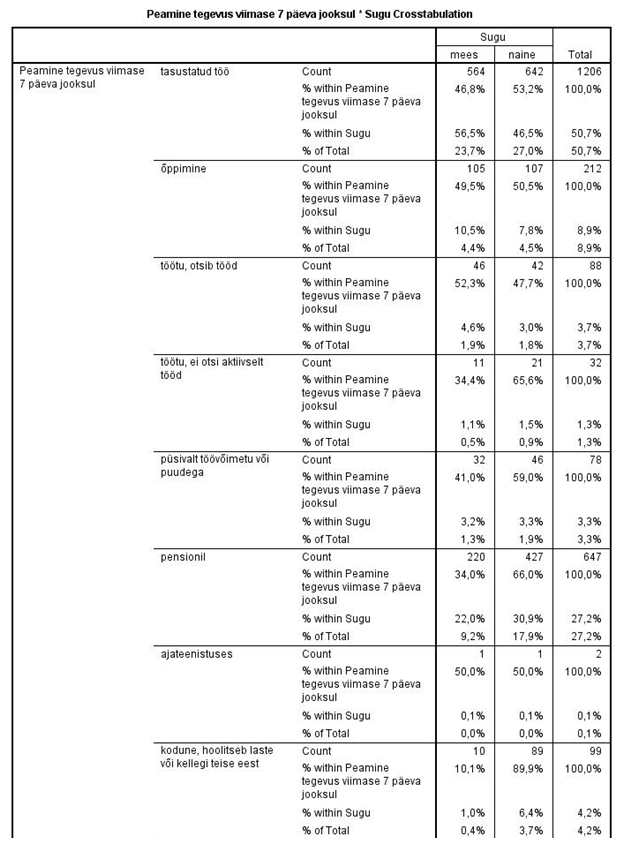
Väljundtabelis („Crosstabulation“, tabel 1) esitatud protsendid on ülevalt alla alati samas järjekorras kui tellimisaknas.
Seega, vastajate hulgas leidus 564 meest, kelle peamiseks tegevuseks oli tasustatud töö.
46,8% nendest, kelle peamiseks tegevuseks oli tasustatud töö, olid mehed.
Meestest 56,5%-l oli peamiseks tegevuseks tasustatud töö.
Üldse oli vastajate koguhulgas selliseid inimesi, kes olid mehed ja ühtlasi ka tasustatud tööl 23,7%.
Tabel 1. Risttabel peamise tegevuse ja soo tunnuste vahel
Risttabeli järel esitatakse tabelid seosekordajatega.
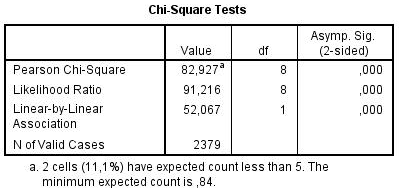
Tabelis 2 pealkirjaga „Chi-Square Tests“ on esimesel real antud hii-ruut-statistiku väärtus (82,927), vabadusastmete arv (8) ja olulisuse tõenäosus (0,000). Seega saab väita, et meeste ja naiste tegevusalade jaotuses on statistiliselt olulisi erinevusi. Millised need erinevused täpsemalt on, tuleb vaadata eelnevast risttabelist.
Märge „a“ hii-ruut-statistiku väärtuse juures näitab väikese vastajate arvuga lahtrite osakaalu. Analüüsitehniliselt oleks oluline, et hii-ruut-statistiku arvutamisel aluseks olevas tabelis ei oleks tühje või väga väikese vastajate arvuga lahtreid.
Tabel 2. Hii-ruut-statistik tabeli esimesel numbrireal.
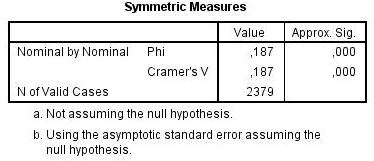
Viimases tabelis (tabel 3) pealkirjaga „Symmetric Measures“ esitatakse statistikute „Phi“ ja Crameri V väärtused (praegusel juhul mõlemad 0,187) ning olulisuse tõenäosus (0,000).
Tabel 3. Crameri V tabeli teisel numbrireal.
Hii-ruut-statistiku ja seosekordajate väärtusi esitatakse sageli teksti sees, märgitakse ära hii-ruut-statistiku väärtus, vabadusastmete arv (df) ja olulisuse tõenäosus.
Näiteks selgus analüüsi käigus, et eri riikide vastajate suhtumine perekonna prioriteetsusesse on statistiliselt olulisel määral erinev, hii-ruut-statistiku väärtuseks on 119,5 (df=12, p=0,000)
Samas võib need lisada ka juba olemasoleva tabeli juurde kas eraldi ridadele või pealkirja/allkirja.
Märksõnad: risttabel, protsent, rea protsent, veeru protsent, üldprotsent, hii-ruut-statistik, Crameri V
