Kui küsida pragmaatikult, millal kasutada statistilise prognoosimudeli koostamiseks mitmetasemelist analüüsi, siis vastab ta, et juhul, kui andmed on korraldatud hierarhiliselt, näiteks üksteises sisalduvate indiviidirühmade kaupa. See lihtsalt on praktiline ja mugav. Kui küsida sama matemaatikult, siis kuuleme, et mitmetasemelist mudelit tuleb rakendada juhul, kui uuritud indiviidid on teatavate rühmade kaupa omavahel seotud, mitte aga üksteisest sõltumatud, nagu nõuab juhuslikult valimilt statistika. Täpsemalt, mitmetasemelist mudelit tuleks kaaluda, kui tunnustevaheline seos rühma sees arvutatuna on tugevam kui erinevate rühmade indiviidide alusel arvutatuna. Indiviidide omavaheline seos võib kaasa tuua vale (alahinnatud) ettekujutuse statistiliste hinnangute  dispersioonist ja selle kaudu ekslikud järeldused mudeli mõjude  statistilise olulisuse   kohta.  Kui küsida sotsioloogilt, miks kasutada mitmetasemelist analüüsi, siis toob ta esmajärjekorras esile vajaduse arvestada tõlgendustes ja tulemuste tähenduse avamisel uurimisobjektide konteksti ja vastastikkusi mõjutusi hierarhilises asetuses olevate indiviidirühmade vahel.  

Mitmetasemelise analüüsi mudeleid tuntakse mitmete nimede all: segamõjudega mudelid, mil lähtekohaks võetakse klassikaline dispersioonanalüüsi mudel (http://samm.ut.ee/dispersioonanalyys), hierarhilised mudelid, mitmetasemelised mudelid  (i. k. vastavalt mixed-effects models, hierarchical linear models, multilevel models). Mitmetasemelised mudelid kerkisid praktikas esile 1970. aastatel.

Mitmetasemelise analüüsi indiviidikogum on hierarhiline ja seda peegeldab ka valimi ülesehitus. Hierarhia eri tasemeil mõõdetakse enamasti ka erinevaid tunnuseid. Klassikaline mitmetasemelise analüüsi näide on haridusuuringud, milles õpilastest (hierarhia madalaim tase) moodustuvad klassid ja klassidest koolid. Õpilast iseloomustavad teistsugused tunnused kui klassi või kooli tervikuna. Inimesed elavad peredes, peredest koosnevad külad või linnajaod, nendest omakorda haldusüksused (vallad ja linnad). Haldusüksust kirjeldatakse näiteks pindala, asustustiheduse ja eelarve suuruse kaudu, küla või linnajagu selle elanike arvu kaudu, peret suuruse, sissetuleku ja laste arvu kaudu. Hierarhia eri tasemete tunnuseid saab mitmetasemelisse mudelisse võtta formaalselt korraga, kuid nende tõlgendus on asjakohane üksnes omal tasemel. Eriti peab tasemete segiajamisest hoiduma juhul, kui tulemuste tõlgendus võiks viia põhjusliku seose esiletoomiseni.

Mida täpsemalt mõistame hierarhia all mitmetasemelise analüüsi mudeleis? Siin oleneb vastus ka konkreetsest algoritmist, mis on seatud mudeli koostamise aluseks. Formaalselt tähendab hierarhia järjestust, mil igal elemendil on üks vahetu eellane ja suvaline arv järglasi (Ü. Kaasik.  Matemaatika leksikon. Tartu 2003). Sellise määratluse alla kuuluvad ka seni toodud näited: õpilane kuulub ühte klassi, kuid klassis võib olla mitu õpilast; iga klass kuulub ühte kooli, kuid koolis võib olla mitu klassi. Analüüsi kontekstuaalsus tekib sellest, et näiteks kooli tunnused võivad seletada klassi tunnuste ja õpilase tunnuste variatiivsust, ja klassi tunnused  õpilase tunnuste variatiivsust. Õpilane tegutseb klassi ja kooli kontekstis, klass kooli kontekstis. Samal ajal loovad õpilased ise klassi eripära ja klassid kooli eripära – mõju võib olla sisu poolest vastastikune.  Mõjude tõlgenduse suund ja võimalus kõnelda mõju põhjuslikust iseloomust on mitmetasemelises mudelis, nagu mis tahes  matemaatilises mudelis, eranditult kontseptuaalne.

 Nimetame andmete ülesehituse veel üht astmelist skeemi – ristklassifikatsiooni – peale eelnevas vaadeldud „pesastruktuuriga“ hierarhia (rühm õpilasi on kooli teinud „pesa“, moodustades klassi, i.k. nested). Ristklassifikatsiooni korral võib teatud taseme indiviid kuuluda järgmisel tasemel ka mitmesse rühma. Nii näiteks järjestust „õpilane – kool – elupiirkond“ vaadeldes ei pruugi kõik õpilased käia elukohajärgses koolis ja erinevatele elupiirkondadele võivad vastata ühed ja samad koolid. Elupaiga omaduste kaudu saab siis vaid osaliselt seletada koolide ja õpilaste omaduste variatiivsust.

Praktikas tähtis hierarhia tõlgendus on longituudandmete (ajas kulgevate kordusmõõtmiste) käsitlust hierarhilisena, mis avab hea võimaluse selle keerulise andmestruktuuri sisukaks analüüsiks. Tõepoolest, võime mõelda nii, et hierarhia madalaima taseme moodustavad longituuduuringu eri voorud, mille tulemused kogunevad „andmepesadena“ uuritud indiviidideks. Esimese taseme indiviidiks on uuringuvooru andmed ja teise taseme moodustavad uuritud indiviidid. Indiviidid on eeldatud olevat üksteisest sõltumatud, kuid ühe ja sama indiviidi mõõtmised eri voorudes võivad olla (ja ilmselt ongi) omavahel seotud. Indiviidi omadused määravad kordusmõõtmiste iseloomu, nt mingi suuruse püsiva kasvu või kahanemise uuringu aja jooksul.

Siinkohal on oluline toonitada asjaolu, mis jääb mõnikord tähelepanuta. Mitmetasemelise analüüsi käigus koostatakse statistiline mudel ja rakendatakse statistilisi mudeli parameetrite hindamismeetodeid. See eeldab, et igal tasemel, ka kõrgematel, on tegemist juhuvalimiga, mille elemendid on üksteisest sõltumatud ja rahuldavad neid nõudmisi, mida juhuslikult valimilt oodatakse (sõltumatus, olenevalt hindamismeetodist juhuslikkuse kindel laad jaotuse poolest jne). Ka peab olema indiviidide arv küllaldane, eriti kõrgematel tasemetel (madalama taseme puhul tuleb indiviidide arv kokku enamasti piisavalt suur). Kui ei ole tegemist ranges mõttes juhusliku valimiga, siis võib muidugi mudeli koostada, aga statistiliste otsustustega (nt mõju statistiline olulisus, hüpoteeside testimine jne) olla väga ettevaatlik.

Kuidas saada lahti andmeis peituvast indiviidide omavahelisest seosest või – otse vastupidi – kuidas seda võimalikult täielikumalt arvestada mudeli koostamisel? Siin võetakse aluseks intuitiivselt lihtne mõte: kui oleme omavahel seotud, siis analüüsigem meid eraldi rühmana nende tunnuste poolest, mis ilmnevad meil üksteisest sõltumatult. Üksteisega seotud indiviidide rühmi vaatleme koos hierarhia kõrgemal tasemel, mille tunnused peegeldavad selle taseme indiviidirühmade omadusi ja seeläbi ka omadusi, mis võivad seletada madalama taseme rühmasisest seost. See tähendab seose käsitluse nihutamist taseme võrra järjest kõrgemale ja eri tasemetel erisuguste mudelite kasutamist. Loomulikult kanduvad kõrgema taseme mudelid indiviidirühmade sisalduvussuhte kaudu madalamale kuni esimesele tasemele välja ja analüüsi tulemuseks saame ikkagi selle, mida esmajoones otsime – indiviidide seas kehtiva seaduspära.

Mudeli koostamine tähendab sõltuva tunnuse variatiivsuse seletuse otsimist variatiivsust prognoosivate tunnuste kaudu. Mitmetasemelisel juhul tähendab see mudeli sõltuva tunnuse hierarhia kõige madalamal tasemel ilmneva hajuvuse  (dispersiooni) lahutamist osadeks: madalaima taseme indiviidide erinevustest tingitud osa pluss järgmise taseme indiviidide  erinevustest tingitud osa ja nii edasi igal järgmisel tasemel. Seejuures võivad sõltuva tunnuse variatiivsust seletavad seaduspärad olla kõrgema taseme rühmiti ka erisugused. Mitmetasemelise mudeli varal saame kõiki neid mudeleid ja dispersiooni osi uurida ühtse metoodika abil, mitte aga tasemerühmi omavahel otseselt kõrvutades või eraldi käsitledes. Võimalik on kaasata ka interaktsioone eri tasemete tunnuste vahel, mis tähendab, et indiviidide hajuvuse seletus madalamal tasemel oleneb sellest, millistesse kõrgemate tasemete rühmadesse need indiviidid kuuluvad ja mis omadustega vastavad tasemerühmad on. Praktikas piirdutakse küllalt sageli kahe tasemega ja seda teeme ka alljärgnevates näite varal antud lähemates selgitustes.

Statistilise iseloomu poolest on tegemist regressioonimudelitega (http://samm.ut.ee/regressioonanalyys), õigemini, nende süsteemiga, mille konkreetne vorm oleneb kasutatavate tunnuste jaotusest. Sõltuv tunnus võib olla niihästi arvuline kui ka  kategoriaalne , sama vaba on ka seletavate tunnuste valik. Tõsi küll, kõik mitmetasemelist analüüsi võimaldavad arvutiprogrammid ei pruugi toetada kõiki sõltuva tunnuse tüüpe, aga suuremad paketid küll. Ka andmekorralduse poolest (hierarhia väljendamise vahendite poolest) on eri programmide puhul erinevusi, seega tasub enne andmestiku lõplikku valmistegemist pakett valida ja asja uurida. Enamasti on üks andmete vorm teiseks korraldatav kergesti.

Milliseid analüüsiviise võiks rakendada hierarhilise andmestiku korral, ilma et pöörduda mitmetasemelise analüüsi poole? Üks võimalusi oleks mudelite koostamine tasemerühmiti, kuid terviklahenduse saamiseks tuleks  rühmade tulemusi siiski kuidagi kokku võtta ja neid omavahel võrrelda. Regressioonimudelite võrdlus ei ole teatavasti aga kergete killast ülesanne. Võiks mudelisse kaasata rühmi määrava tunnuse ja selle interaktsioonid seletavate tunnustega, kuid see ei kõrvalda mõõtmiste omavahelist seost ja muudab ka mudeli kohmakaks ja keeruliseks. Andmestiku võiks „asendada“ ühetasemelise andmestikuga, milleks on kõrgeimale tasemele agregeeritud andmestik (näiteks elanike tunnuste keskmistest koosnev linnajao või valla andmestik, indiviidiks vald või linnajagu) või vastupidi, tuua madalama taseme iga indiviidi juurde vastav kõrgema taseme tunnus (iga elaniku üheks tunnuseks on ka tema küla või linnajao elanike arv). Agregeerimine võib viia nn ökoloogilise eksijärelduseni (i.k. ecological fallacy), sest seaduspära indiviidi tasemel teatud tunnuste vahel ei pruugi olla sama mis nendesamade tunnuste vahel agregeeritud andmetes. Pisut etteruttavalt: allpool kasutame näitena õpilase keskmise koolihinde mudelit kaheastmelises hierarhias: õpilane-kool. Muuhulgas vaatleme koolihinde seost sellega, kui tõepärane on õpilase arvates õpingute jätkamine ülikoolis. Õpilaste individuaalsete andmete alusel saame korrelatsioonikordaja 0,54 (üks tunnus kirjeldab teise variatiivsusest vähem kui 30%), kuid koolide agregeeritud andmeil märgatavalt tugevama seose, nimelt 0,85 (agregeerimine tähendas vaadeldavate koolide keskmise arvutust kummagi tunnuse puhul, vastastikuse kirjelduse aste üle 70%). Samalaadset mõtet väljendab nn Simpsoni paradoks (https://en.wikipedia.org/wiki/Simpson’s_paradox) ja mitmed näited ökoloogilise eksijärelduse kohta (vt nt J. Hox. Multilevel Analysis: Techniques and Applications. Routledge,  2002, lk 3). Vastupidine mõttekäik – disagregeerimine – tähendab nn atomistlikku eksijäreldust (i. k. atomistic fallacy), mil kõrgema taseme tunnuse üks ja sama väärtus suurendab madalama taseme rühma sisest seotust veelgi.

Tänasel päeval on mitmetasemeline analüüs levinud analüüsimeetod ja raske oleks leida valdkonda, kus ei püüta seda rakendada. Võiks öelda, et meetodi algkodu on haridusuuringute alal (hierarhia kool-klass-õpilane), kuid viimasel ajal leiab selle meetodi kohaseid rohkeid katseid kultuuridevahelistest uuringutest (hierarhia elukohamaa-elanik). Sisukaid rakendusi tuleb longituuduuringutest (hierarhia inimene-ajamoment). Lisame allpool mõned viited ja edasiviited, mis sobivad kasutamiseks nii teoreetilisema kui ka praktilisema kallakuga huvilistele.

Lahendused SPSS abil (+ hulk viiteid):

http://www.ats.ucla.edu/stat/spss/topics/MLM.htm

Sissejuhatav ülevaade Bristoli ülikooli mitmetasemelise analüüsi keskusest Centre for Multilevel Modelling:

http://www.bristol.ac.uk/cmm/learning/multilevel-models/

 Sageli tsiteeritav tekst praktilise rakenduse asjus paketi SPSS abil:

Peugh, J.L., Enders, C.K. (2005) Using the SPSS mixed procedure to fit cross-sectional and longitudinal multilevel models. Educational and Psychological Measurement, Vol 65, No 5, 717-741,  vt  http://epm.sagepub.com/cgi/content/abstract/65/5/717 

Euroopa sotsiaaluuringu metoodiliste materjalide veebivärav:

http://essedunet.nsd.uib.no/ ,  Multilevel models

Raamatuid:

 Ronald H. Heck, Scott L. Thomas, Lynn N. Tabata. Multilevel and Longitudinal Modeling with SPSS. Routledge, Taylor&Francis, 2^nd ed, 2014.

 Stephen W. Raudenbush, Anthony S. Bryk. Hierarchical Linear Models: Applications and Data Analysis Methods (Advanced Quantitative Techniques in the Social Sciences). Sage Publ, 2^nd ed, 2002.

 Sophia Rabe-Hesketh and Anders Skrondal. Multilevel and Longitudinal Modeling Using Stata. Stata Press, 2^nd ed, 2008.

 Joop Hox. Multilevel Analysis. Routledge, Taylor&Francis, 2^nd ed, 2010.

 Ühe mitmetasemelise analüüsi piltliku selgituse leiab aadressilt:

http://www.pitt.edu/~super1/lecture/lec6191/008.htm.

 Mitmetasemelise analüüsi tarkvara on olemas igas suurema programmipaketis ja lisaks on loodud veel eripakette. Nimetagem mõned võimalused.

 SAS – Proc Mixed  http://support.sas.com/resources/papers/proceedings13/433-2013.pdf

 SPSS – Mixed Models

ftp://public.dhe.ibm.com/software/analytics/spss/documentation/statistics/23.0/en/client/Manuals/IBM_SPSS_Advanced_Statistics.pdf

 Stata  http://www.stata.com/features/overview/multilevel-generalized-linear-models/

 MlWin   http://www.bristol.ac.uk/cmm/software/mlwin/

 R     https://cran.r-project.org/doc/contrib/Bliese_Multilevel.pdf

 MPlus  https://www.statmodel.com/usersguide/chapter9.shtml

Ja paljud teised.

Käesolevas õppematerjalis tutvustame mitmetasemelise analüüsi mõtet näitega arvulisel skaalal mõõdetud sõltuva tunnuse analüüsimisest. Idee jääb püsima ka muud tüüpi sõltuva tunnuse jaoks, aga arvtunnuse mudel tundub sissejuhatavalt lihtsam ja samuti on arvtunnuste regressioonimudelid praktikas laiemalt levinud. Piirdume alustuseks andmete hierarhia kahe tasemega. Rõhutame ka, et enne mudeli koostamisele asumist peab uurijal olema läbi mõeldud selge analüüsiplaan − hüpoteeside süsteem ja kontseptuaalne mudel, mille kohaselt uuritav nähtus toimib. Ilma selleta võib nii keeruline meetod, nagu on mitmetasemeline analüüs, anda formaalselt suurepärase, kuid sisutühja tulemuse.

Näidetes kasutame paketi SPSS mooduli Mixed models – Linear lahendusi. Algandmed on korrastatud viisil, mil kõrgema taseme tunnuse väärtus on salvestatud madalama taseme iga indiviidi juurde (tavaline ristlõikeandmestik, vt nt Peugh ja Enders 2005, http://epm.sagepub.com/cgi/content/abstract/65/5/717 hierarhilise andmestiku sellisele kujule viimiseks SPSS käsu Merge Files abil).

Näite ”legend” on järgmine. Haridusjuhtidele pakub huvi koolihinde kujunemine ja eriti see, kuivõrd oleneb koolihinne õpilase ja õpetaja suhtluslaadist. Uuriti koolide juhuvalimit ja igas valitud koolis juhuslikult valitud klasse 9. ja 10. klasside seast. Küsitleti kõiki väljavalitud klassi õpilasi. Koole oli 57 ja keskmine õpilaste arv kooli kohta tuli 60 (standardhälve 35). Õpilaste üldarv on (olenevalt lünklikkusest konkreetsetel tunnustel) 3600 ringis.

Kasutame oma näites järgmisi tunnuseid.

1. Eri õppeainete hinnete alusel saadud üldistatud koolihinne skaalal 0 kuni 5, mis on teataval kindlal viisil kaalutud üksikõppeainete aritmeetiline keskmine. Hinde sagedusjaotus  joonisel 1  on silma järgi otsustades heas kooskõlas normaaljaotusega. Üldkeskmine hinne on 3,02 standardhälbega 0,69, seega skaala füüsilisest keskpunktist kõrgem. Joonisel 2on kujutatud keskmist hinnet koolides koos usaldusvahemikuga usaldusnivool 99%. Leidub koole, mille keskmised on statistiliselt selgelt erisugused (isegi kui arvestame Bonferroni efekti  võimalust nii suure hulga usaldusvahemike kõrvutamisel). Seega võib arvata, et koolides valitseb teatav eripära koolihinde kujunemisel.
2.  Sugu: 1 – noormees (54%), 2 – tütarlaps; noormeeste keskmine hinne on 2,90 ja tütarlastel 3,15.
3. Läbisaamine õpetajatega; õpilaselt küsiti skaalal 1 kuni 5, kui sageli tuleb ette halba läbisaamist õpetajatega, kus kood 1 tähendas sagedast ja 5 väga harva ette tulevat halba suhet (keskmine 4,3, st lähedal halva läbisaamise täielikule eitamisele, standardhälve 0,95).
4. Kooli iseloomustav üldine hoiak õpingute jätkamiseks ülikoolis; õpilaselt küsiti skaalal 1 kuni 5, kui tõenäone on tema puhul õpingute jätkamine ülikoolis, kus kood 1 tähendas, et väga ebatõenäone, ja 5 – väga tõenäone. Kooli üldine hoiak (edasiõppimise ”indeks”) saadi selle kooli õpilaste edasiõppimise tõenäosuslikkuste keskmisena, st agregeeritud tunnusena. ”Indeksi” väärtused varieeruvad 1,5 ja 3,2 vahel keskmisega 2,2 ja standardhälbega 0,4. Rõhutame taas, et agregeeritud tunnuse kaudu väljenduv seaduspära on kooli taseme seaduspära, mis ei pruugi ühtida õpilase taseme seaduspäraga.

Põhjustel, mida selgitame allpool õiges kohas, tsentreerisime nii õpetajatega läbisaamise tunnuse kui ka õpingute jätkamise tunnuse (indeksi) oma üldkeskmise suhtes (lahutasime vastavalt iga õpilase ja iga kooli väärtusest üldkeskmise).  Lisame veel, et andmestikus on reaalsed, kuid kohandatud andmed, mistõttu meie analüüsi ei saa pidada päris haridusuuringuks.

Andmetel on selge hierarhiline iseloom: kool – klass – õpilane. Ülesande lihtsustamiseks jätame klassi taseme vahele ja käsitleme õpilaste rühmitust üksnes kahetasemelisena, st koolide kaupa. Statistilise mudeli poolest on meil mitu ülesannet:

• hinnata üldiselt koolide keskmise hinde muutlikkust (allpool mudel 5, ainult konstanti sisaldav mudel),
• välja selgitada, kuivõrd kujundab õpilase hinnet õpetajatega läbisaamine ja kuivõrd erinevad tütarlaste ja noormeeste hinded (allpool mudelid 1 ja 3; õpilase taseme tunnused),
• leida, kuivõrd seletab õpilase individuaalsete tegurite toime erinevusi koolide vahel koolis levinud hoiak edasiõppimise suhtes (mudelid 2 ja 4, 6; õpilase ja kooli taseme tunnused ning nende interaktsioon; kas edasiõppimisele enam orienteeritud koolides on õpetajatega läbisaamine hinde tugevam mõjutegur kui vähem orienteeritud koolides).

Neid ülesandeid saame lahendada mitmetasemelise mudeli abil: leiame hinde regressioonimudeli ülejäänud tunnuste kaudu, kaasates interaktsioonitegurid eri taseme tunnuste vahel (kooli tunnuse interaktsioon õpilase tunnusega) ja uurime, kuidas jaotub hinde variatiivus hierarhia eri tasemete vahel (õpilase eripära, kooli eripära). Kui tasemeid oleks rohkem kui kaks, siis saaks analoogilist variatiivsuse lahutamist eri tasemete vahel ja eri tasemete tunnuste kombineerimist jätkata analoogilisel viisil, kuid ülesande maht kasvaks väga kiiresti.

Vaatleme järgmisi mudeleid:

Mudel 1 – hinde prognoos sootunnuse kaudu, sootunnuse regressioonikordaja võib koolides olla erisugune.

Mudel 2  – hinde prognoos sootunnuse kaudu, mille kordajat prognoositakse õpingute jätkamise mõtte levimuse kaudu koolis, sootunnuse regressioonikordaja võib olla koolides erisugune.

Mudel 3  – hinde prognoos õpetajatega läbisaamise hinnangu kaudu, regressioonikordaja võib koolides erisugune.

Mudel 4  – hinde prognoos õpetajatega läbisaamise hinnangu kaudu, mille kordajat prognoositakse õpingute jätkamise mõtte levimuse kaudu koolis; regressioonikordaja võib olla koolides erisugune, 

Mudel 5 – mõjuteguriteta mudel, konstantne prognoos.

Mudel 6 –  kokkuvõtlik mudel; hinde prognoos sootunnuse ja õpetajatega läbisaamise hinnangu kaudu, mille kordajaid prognoositakse õpingute jätkamise mõtte levimuse kaudu koolis.

Mudelid 1 ja 3 ning 2 ja 4 on ülesehituselt sarnased.

Põhikäsud mitmetasemelise mudeli koostamiseks paketi SPSS abil:

Mixed Model – Linear

Subjects – teise taseme gruppe määrav tunnus (muidugi võib olla ka enam kui kaks taset)

Dependent variable – tunnus, mille prognoosimiseks mudel koostatakse

Factors – kategoriaalsed seletavad tunnused

Covariates – pidevad seletavad tunnused

Fixed – märkida mudelisse tulevad tunnused; valida Include intercept vabaliikmete esiletoomiseks

Random – märkida juhuslikena käsitletavad tunnused; valida kovariatsioonimaatriksi tüüp ; valida Include intercept

Estimation – valida suurima tõepära meetod Maximum likelihood ML või Restricted maximum likelihood REML Vt hindamismeetodi valiku kohta siit

Statistics – valida Descriptive statistics vajaduse korral, Parameter estimates regressioonikordajate esiletoomiseks; Test for covariance parameters hüpoteesi kontrollimiseks dispersioonide kohta

Save – valida vajadusel prognooside ja prognoosijääkide salvestamine.

 Ülesanne: anda hinde prognoos sootunnuse kaudu, mille regressioonikordaja võib koolides erineda.

 Koostame järgmise skeemi kohase mudeli:

hinne koolis j õpilasel i = vabaliige  koolis j + b_1j ∙ kooli j õpilase i sugu + viga õpilase i puhul koolis j,            (1a)

vabaliige koolis j = vabaliikme keskmine + vabaliikme viga kooli j puhul,                        (1b)

b_1j = regressioonikordaja b_1j keskmine + kordaja b_1j viga kooli j puhul.                (1c)

Avaldised 1a-1c moodustavad meie ülesandele vastava regressioonivõrrandite süsteemi. See väljendab oletusi, et hinne noormeestel ja tütarlastel võib erineda, sealjuures eri koolides erisugusel määral ja viisil (sootunnuse regressioonikordaja võib olla kooliti erisugune, avaldis 1c) ning koolide üldine hindetase võib olla erinev (seda peegeldab vabaliige, avaldis 1b). Kui vead oleksid statistiliselt tühised (ja regressioonikordajad statistiliselt olulised), siis saaksime kõigi koolide jaoks ühise adekvaatse regressioonimudeli.

Kirjutame avaldised 1a-1c üles ka üldistes tähistustes. Üldine tähistus on selle meetodi puhul mõistlik ja sellega tasub harjuda, sest vähegi keerulisema mudeli puhul kaob muidu igasugune ülevaade regressioonivõrrandite süsteemist.

Vaatleme kahetasemelisi andmeid, kus teisel tasemel eristame k tasemerühma. Olgu Y sõltuv tunnus, mille väärtuseks tasemerühmas j indiviidi i korral on Y_ij, i = 1, 2, …, n_j, j = 1, 2, …, k.  Teise taseme valimimaht on k ja esimesel tasemel n = n₁ + n₂ + … + n_k. Vaatleme mudelit kujul (näites avaldis 1a)

ja eeldame, et mudel on keskmiselt õige, st jääkliige e_ij on keskmiselt 0. Tunnus X on esimesel tasemel mõõdetud tunnus (nagu ka sõltuv tunnus Y), mis meie ettekujutuse kohaselt võiks seletada esimesel tasemel sõltuva tunnuse variatiivsust. Eeldame veel jääkliikmete e_ij jaotust ligikaudu normaaljaotuse kohaselt keskmisega 0 ja omavahelist sõltumatust. Mudeli täpsust aitab hinnata jääkliikme dispersioon. Kui see on väike (nullilähedane), siis ei leidu suuri vigu ja mudel on statistiliselt sobiv. Kui vea dispersioon on statistiliselt oluliselt nullist erinev, siis ei saa mudelit pidada tegeliku seaduspära heaks lähendiks. Vaadeldavat mudelit mõistetakse sellise alltekstiga, et regressioonikordajad võivad olla teise taseme tasemerühmiti erisugused, mida väljendatakse veakomponendiga vastavates regressioonimudelites. Vaatleme esialgu regressioonikordajate β esitust üksnes vabaliikmest sõltuvate mudelite kaudu (näites vastavalt avaldised 1b ja 1c):

Nendes võrrandites näitavad mudelite vabaliikmed γ keskmist regressioonikordajat (ka vabaliige on regressioonikordaja, aga ”vabalt”, tunnuseta), sest vead u loetakse keskmiselt nulliks (ja normaaljaotuse lähedasteks oma jaotuse poolest). Tasemerühmade parameetritele β ühise konstantse prognoosi sobivuse üle saame otsustada veakomponendi dispersiooni alusel: kui see on statistiliselt null, siis oleme saanud tasemerühmade parameetrite hea esituse keskmiselt eespoolesitatud kujul.

Kokkuvõtlikult, kordajate β prognoosivõrrandeid sõltuva tunnuse Y prognoosivõrrandisse asendades oleme saanud järgmise mudeli:

Selles regressioonivõrrandis on nn fikseeritud osa (esimesed kaks liiget, ei sisalda veakomponente) ja nn juhusliku osana individuaalseid tasemerühma siseseid erinevusi arvestav komponent e_ij, tasemerühmade erinevusi arvestavad komponendid u_0j ja u_1j, seejuures seotuna teise taseme rühmade eripära seletamiseks valitud tunnusega. Seega prognoosiviga oleneb esimese taseme tunnuse väärtusest. Fikseeritud osa annab statistilise keskmise hinnangu. Vaatame läbi näiteülesande põhitabelid selle mudeli korral.

Tabelis 1.1 on esitatud mudeli iga fikseeritud osa liikme kohta dispersioonisuhte testi tulemused (i.k. variance-ratio test, kriteeriumiks on sõltuva tunnuse dispersioonist mõjuteguriga ärakirjeldatud dispersiooniosa ja kirjeldamata jäänud dispersiooniosa suhe). Nullhüpoteesiks, mida kontrollitakse, on oletus vastava liikme mõju puudumisest (nulliga võrdumisest) mudelis. Otsus tehakse F-suhte põhjal, kasutades teoreetilist F-jaotust tabelis osutatud vabadusastmete arvude korral.  Osutatakse nullhüpoteesi olulisuse tõenäosus, mille alusel meie ülesandes võime praegu kinnitada olulisuse tõenäosusega alla 0,0005 sootunnuse statistilist mõju mudelis, lihtsamini öeldes, tütarlaste ja noormeeste hinnete erinevust keskmiselt. Kui suur on see erinevus, seda näeme regressioonikordajate tabelist 1.2.

Tabelis 1.2 esitatakse fikseeritud mõjude kokkuvõte. Tütarlaste hinne on keskmiselt 0,25  võrra kõrgem kui noormeestel (vahe usaldusvahemik usaldusnivool 95% on 0,20 kuni 0,30). Noormeeste hinne koolides keskmiselt on 2,90 (2,83…2,97). Kontrollitakse hüpoteesi regressioonikordajate nulliga võrdumise kohta, kasutades regressioonikordaja ja selle standardhälbe suhet ehk t-statistikut (nt 9,6 = 0,251/0,026; erinevused võivad tulla ümardamisest), mis osutatud vabadusastmete arvu korral peaks nullhüpoteesi kehtimisel jaotuma t-jaotuse kohaselt. Olulisuse tõenäosus alla 0,0005 näitab käesoleval juhul selle hüpoteesi paikapidamatust ja regressioonikordajate statistilist olulisust. Sugu saab pidada statistiliseks hinnete eristajaks olulisuse tõenäosusega alla 0,0005.

Seda, kui suur osa hinnete individuaalsest varieeruvusest jääb seletamata ja seda, kuivõrd sobivaks saab pidada tabelis 1.2 antud regressioonimudelit ühtsena kõigi koolide jaoks, näitab tabel 1.3.

Esimese taseme indiviidide seas on dispersiooni määraks ehk jääkdispersiooniks, mida vaadeldav mudel ei väljenda, 0,396 standardhälbega 0,0097, mis annab suhtena Waldi statistiku 41,0. Waldi statistikut kasutatakse nullhüpoteesi „jääkhajuvus on null“ kontrollimiseks. Kui seda hüpoteesi ei ole alust kummutada, siis võiksime mudeli lugeda sõltuva tunnuse muutlikkust ammendavalt käsitlevaks mudeliks hierarhia esimesel tasemel. Selles ülesandes tuleb hüpotees kummutada olulisuse tõenäosusega alla 0,0005. Usaldusvahemik usaldusnivool 95% näitab samuti, et jääkhajuvus on kaugel nullist (0,38 …0,42). Seega mudelit tuleks esimese taseme seletavate tunnuste poolest veel rohkesti edasi arendada, et vea hajuvust nulli ümber vähendada.

Vaadeldav mudel sisaldab kooliti muutuda võiva vabaliikme ja kooliti muutuda võiva kordajaga sootunnuse. Kuivõrd osutuvad vabaliige ja regressioonikordaja muutlikuks koolist kooli liikudes, sellest annavad aimu tabelis 1.3 olevad kooli taseme võrrandite vigade dispersioonid. Arv UN(1,1) väljendab vabaliikme vea dispersiooni, arv UN(2,2) soo regressioonikordaja vea dispersiooni ja arv UN(2,1) kovariatsiooni vabaliikme ja sootunnuse regressioonikordaja vahel. Iga äsjanimetatud komponendi korral kontrollitakse hüpoteesi selle komponendi võrdumise kohta nulliga, mis kehtides tähendaks seda, et viga on tühine, sest ei varieeru kuigi palju oma keskmise ümber, mis on eelduse kohaselt null. Tähistuse UN (unstructured) taga on meie valik, milliseks peame mudeli komponentide omavahelist seost (vt kovariatsioonistruktuuri valik) – jätsime praegu täiesti lahtiseks, lubades komponentidel (vabaliige, sootunnuse regressioonikordaja) omavahel ka korreleeruda ja hinnates kõiki dispersioone ja kovariatsioone. 

Näeme, et vabaliikme vea dispersioon on statistiliselt oluliselt nullist erinev olulisuse tõenäosuse korral, mis jääb alla 0,0005. See tähendab, et koolide vabaliikmed  varieeruvad keskmise ümber olulisel määral, kusjuures eeldame, et nende jaotuseks on normaaljaotus (praegu keskmisega 2,90 ja dispersiooniga 0,0546 ja sellest ruutjuurt võttes, standardhälbega 0,234). Ühine vabaliige 2,90 ei sobi kõigile kuigi hästi. Küll aga ei ole alust pidada sootunnuse regressioonikordajat statistiliselt oluliselt varieeruvaks, sest selle dispersioon on väga väike ja statistiliselt eristumatu nullist (olulisuse tõenäosus 0,23). Tütarlaste ja noormeeste hinnete keskmine erinevus on koolides statistiliselt üks ja sama 0,25 hindepalli ümber. Näeme ka, et vabaliige (meie mudelis noormeeste keskmine hinne) ja sootunnuse kordaja ei ole omavahel korreleeritud statistiliselt olulisel määral (olulisuse tõenäosus 0,66). Kui nad oleksid seda, nt negatiivses korrelatsioonis, siis tähendaks see, mida kõrgem on noormeeste hinnete tase, seda keskmiselt väiksem on erinevus tütarlaste hinnetest.

Tabeli 1.4 tõlgendamiseks peaks meil olema käepärast mõni teine samalt andmestikult koostatud mudel, mis oleks arendatud käesolevast mudelist mõjutegurite juurdelisamise või ärajätmise teel. Sel juhul vahe, mis tekib tõepärafunktsioonide vahel, aitaks iseloomustada tehtud muudatuse statistilist olulisust. Kui mudelit arendades õnnestub sobitusastme mõõtusid vähendada, siis on see olnus liikumine suurema  sobitusastme suunas. Sõna „kriteerium“ asemel võib siin rahulikult öelda ka „kordaja“, nt Akaike kordaja.

Mudeli sobitusaste.  Mudeli analüüsimisel tuleb silmas pidada, esiteks, seda, et mudelisse võetud mõjud oleksid statistiliselt olulised mingil praktikas vastuvõetaval olulisuse nivool (vähemalt osa neist) ja samuti sisu poolest tähenduslikud (mitte väga nõrgad). Teiseks, mudeli arendamisel tuleks liikuda mudeli sobitusastme kasvamise suunas. Mudeli sobitusastet hinnatakse mitmete sobitusastme kordajate kaudu, mis enamasti põhinevad tõepärafunktsioonil, mis selle mudeli korral saavutatakse. (Meenutame, et väga lihtsa ettekujutuse kohaselt on tõepärafunktsioon kasutada oleva valimi saamise tõenäosus, kui eeldame sõltuva tunnuse juhuslikkuse teatavat kindlat kuju, nt normaaljaotust). Tõepärafunktsiooni väärtus on tõlgendatav suhteliselt, üht mudelit teisega võrreldes. Mida väiksem tuleb sobitusastme kordaja väärtus, seda parema mudeli oleme saanud (seda lähemal on tõepärafunktsiooni väärtus arvule 1 ehk kindla sündmuse tõenäosusele – valimi saamine on toimunud sündmus). Selgituseks lisame, et tõepärafunktsiooni L väärtust vaadeldakse enamasti logaritmskaalal (ln L, miinusarvud seega ja sellest miinusmärk sobitusastme kordajates).  Sagedasimad sobitusastme kordajad on Akaike informatsioonikriteerium (kasutame lühendit AIC) ja Schwarzi-Bayesi informatsioonikriteerium (BIC), mis on suuruse poolest võrreldavad mis tahes mudelite korral vaadeldavas tunnusruumis. Tõepärafunktsiooni väärtused on omavahel võrreldavad sel juhul, kui üks mudel on saadud teisest tunnuste ärajätmise või juurdevõtmise teel (st üksteises ”sisalduvate” mudelite korral). Lisame veel ka kordajate AIC ja BIC arvutuseeskirja, et täpsustada nende tähendust. Neid kordajaid nimetatakse ka informatsiooniteoreetilisteks kriteeriumideks ja selle taga on teoreetiline põhjendus. Võiks väga vabas sõnastuses öelda nii, et kordaja mõõdab infokadu, mis tekib reaalse protsessi asendamisel meie mudeliga. Mida väiksem kadu, seda parem mudel. Akaike kordaja oleneb peale tõepärafunktsiooni mudelis hindamist vajavate parameetrite arvust m:

Kui kaks mudelit annavad sama tõepärafunktsiooni väärtuse, aga ühes on rohkem seletavaid tunnuseid kui teises, siis tuleb Akaike kordaja selles mudelis suurem, kus on rohkem seletavaid tunnuseid (”karistus” tunnustega pillava ümberkäimise eest). Veel karmim on Schwarzi kordaja, milles ”karistatakse” ka suure indiviidide arvu n eest:

Kui sama tõepärafunktsiooni väärtus on saadud suurema indiviidide arvu korral, siis tuleb BIC suurem. Ka tunnuste arv suurendab seda kordajat.  Kordaja CAIC on konsistentne Akaike kriteerium, st teatav paremate statistiliste omaduste nimel tehtud  modifikatsioon esialgsest kordajast. Vahed ei ole praktiliselt suured, aga teoreetiliseks diskussiooniks mõnikord piisavad.  Kordaja AICC on Akaike kordaja modifikatsioon väikese valimi korral. Kui mudeli parameetrite hulk m on väike võrreldes valimimahuga, siis ei tule vahet:

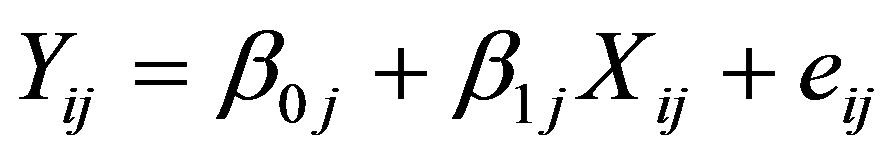
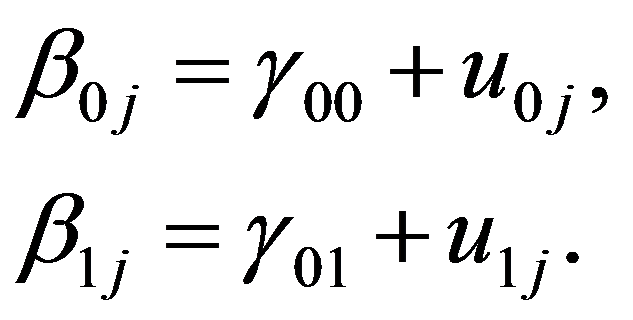
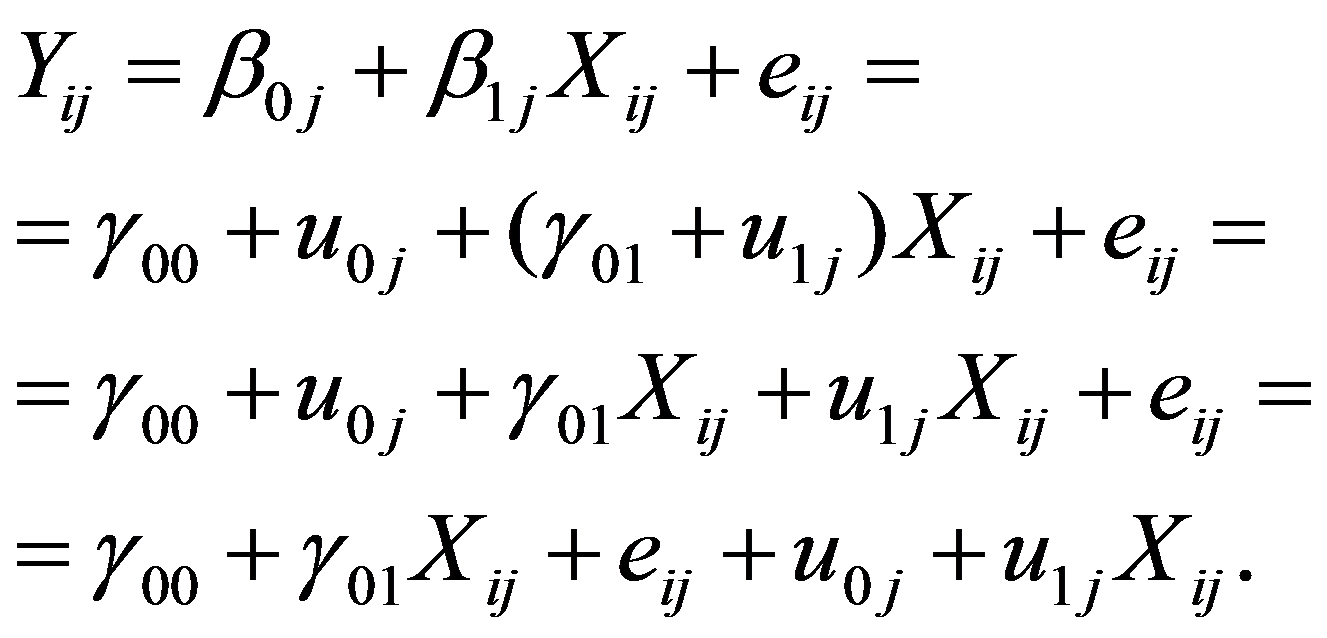
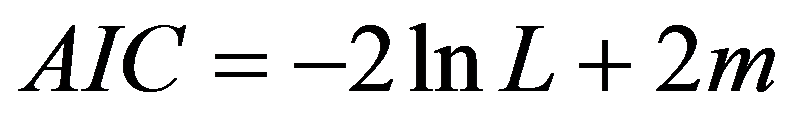
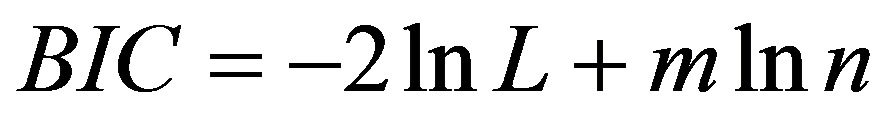
Lähtume analüüsi konteksti mõttest ja uurime, kuivõrd võiks koolide erisugust hindetaset seletada sellega, milline on koolis valitsev hoiak õpingute jätkamise suhtes. Püüame seletada teise taseme (kooli taseme) varieeruvust ülikooliõpingute tõepärasuse astme kaudu. Seda tunnust käsitleme tsentreeritult, st selle nullpunktiks on koolide keskmine tõepära jätkata ülikooliõpinguid (esialgne skaala „1-väga ebatõenäone jätkata ülikoolis“ kuni „5-väga tõenäone jätkata ülikoolis“).

Üldises tähistuses vaatleme järgmist võrrandisüsteemi:

Tunnus Z on teise taseme tunnus ja seepärast ei ole sel tähistuses indiviidi indeksit i, vaid ainult kooli indeks j. Tunnus Z prognoosib meie ettekujutuse kohaselt omakorda regressioonimudeli alusel niihästi vabaliiget kui ka regressioonikordajat esimeses mudelis. Avaldisi üksteise asetades saame järgmise lõppmudeli:

Nagu mudelis 1, on ka mudelis 2 kaks osa – fikseeritud osa (esimesed neli liidetavat) ja juhuslik osa (viimased kolm liidetavat). Mudelit koostama minnes tuleb tähele panna, et mudelisse kuulub nüüd esimese ja teise taseme interaktsiooni komponent regressioonikordajaga γ_11. Muus osas on tehniliselt kõik samasugune, mis eelmises mudelis. Märkame ka, et mudeli juhuslik osa sisaldab seletavaid tunnuseid ja mudeli viga oleneb nende väärtustest.

Hoiak õpingute jätkamise suhtes osutub koole hinde poolest eristavaks tunnuseks, kuid mitte interaktsioonis sootunnusega (tabel 2.1). Interaktsioonitegur on statistiliselt mitteoluline mis tahes mõeldava olulisuse nivoo korral ja seega koolis valitsev hoiak õpingute jätkamise suhtes toimib hinde suhtes noormeestel ja tütarlastel ühetaolisel määral regressioonikordajatega, mida näeme tabelist 2.2 Mida levinum on edasiõppimise mõte koolis, seda kõrgem tuleb kooli hindetase (vabaliige esimese taseme mudelis). Sootunnuse ja edasiõppimise hoiaku interaktsioonitegur on positiivne, aga väga väike ja statistiliselt ebaoluline. Positiivne kordaja (oletagem, et statistiliselt tähendusrikas) tähendaks seda, et tütarlaste hinnet mõjutab edasiõppimise mõtte laiem levik koolis enam kui noormehi. Aga nii praegu öelda ei saa (olulisuse tõenäosus 0,71). Regressioonikordajate tõlgenduseks saame lisada, et tütarlaste keskmine hinne keskmise edasiõppimise tõepärasusega koolides (tsentreeritud tunnuse väärtus 0) on 0,24 võrra kõrgem kui poistel (sootunnuse peamõju regressioonikordaja). Samuti saame öelda, et poistel (koodväärtus 0) on koolides, kus edasiõppimise tõepära on punkti võrra kõrgem, keskmine hinne kõrgem 0,35 võrra. Tsentreerimise mõte on tõlgendusvõimaluste laiendamine.

Tabeli 2.3 varal saame uurida, kuivõrd vähenes koolikonteksti arvestamise teel hinnete dispersioon kooli tasemel. Kõigepealt paneme tähele, et õpilase taseme jääkdispersioon on jäänud samaks, nagu oli mudelis 1, mis nii peabki olema, sest me ei võtnud kasutusele ühtki uut õpilase taseme prognoosivat tunnust. Ettearvatult ei ole ka muutunud soo regressioonikordaja statistiliselt mitteoluline vea dispersioon UN(22), sest olematut muutlikkust ei ole võimalik prognoosida. Ka kovariatsioon U(2,1) on praktiliselt sama ja väga nõrk. Vabaliikme dispersioon on vähenenud 0,0546 – 0,0132 = 0,041 võrra ehk 75% esialgsest väärtusest. Hoiak ülikooliõpingute jätkamise suhtes on vettpidav variatiivsuse seletaja koolide seas.

Koolikonteksti arvestamine muudab mudeli 2 ka sobitusastme poolest paremaks mudelist 1. Näeme tabelist 2.4 , et kõik sobitusastme mõõdud on vähenenud (protsentuaalselt kahjuks väga vähe).  

Lisame saadud mudeli illustreerimiseks mõned joonised mudeli 2 abil saadud prognooside kaudu. Joonisel 3 on näha hinde prognoos noormeestel ja tütarlastel prognoosipunkte ühendavate sirgete kimbuna. Igal koolil on oma joon. Näeme, et ilma erandita suunduvad jooned  alt ülespoole, kuid mitte päris ühesuguse kaldega. Selles peegeldub sootunnuse regressioonikordaja minimalistlik muutlikkus koolide lõikes (vt tabelis 2.3) komponenti UN(2,2)).

Joonis 4 illustreerib edasiõppimise hoiaku ja hinde mudelipärast seost hinde prognooside kaudu. Tegemist on küll  hüpliku (koolide veakomponendid on arvesse võetud), kuid siiski visa seaduspäraga: intensiivsema edasiõppimise mõtte levikuga koolis kaasneb kõrgem hinne. Seda, et interaktsiooni sootunnuse ja edasiõppimise hoiaku vahel statistiliselt ei olnud, näeme noormeeste ja tütarlaste üsna sarnaste joontena.

Joonisel 5  on kujutatud keskmise hinde muutlikkust mudeli fikseeritud osa kaudu saadud prognooside abil. Graafik on mõistagi ühtlasem ‒ esimese taseme prognoosivead on jäetud kõrvale.  Joon on justkui kahekäiguline: väga vähelevinud edasiõppimise mõtte piirkond (vasak serv), kus iga punkt kasvu kasvatab hinnet jõudsalt, ja parempoolne, leigem sõltuvus.

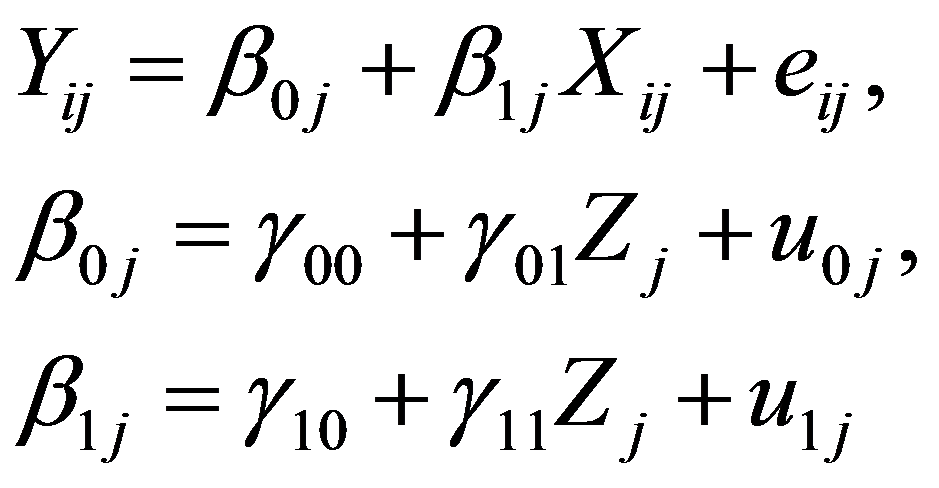
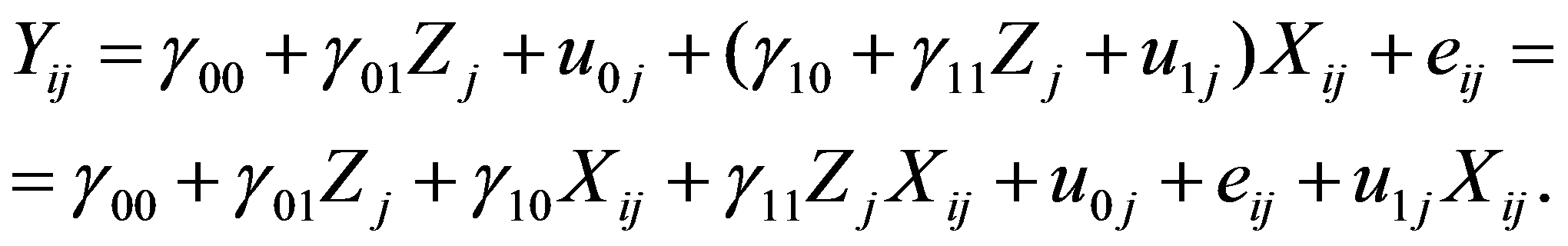
Meie näitesse valitud napis tunnuste varus on veel üks õpilase omadus, mille varal tüüpmõtlemisele tuginedes võiks kindla peale välja minna: õpetajatega halb läbisaamine toob kaasa halvad hinded. Sellel „seaduspäral“ on ilmselt mitmeid põhjusi, ka ratsionaalseid, aga siinkohal uurime, kuidas meie meetod selle tavateadmisega toime tuleb. Andmestikus olev õpilase kommunikatiivseid oskusi peegeldav tunnus väljendab seda, kui sageli tuleb ette halba suhet õpetajatega: 1 – alatasa kuni 5 – mitte kunagi või väga harva. Ei saa vahest ütelda, et see tunnus mõõdab suhete headust – pigem halbade suhete puudumist (kusagil vahel on ka neutraalsus või jäine ükskõiksus). Ka läbisaamise tunnus on tsentreeritud üldkeskmise suhtes. Koostame esmalt mudeliga 1 analoogilise mudeli, oletades läbisaamise tunnuse mõju võimalikku muutlikkust kooliti (mudel õpilase taseme regressioonikordaja prognoosimiseks) ja loomulikult lubades hinde muutlikkust koolide lõikes (mudel  õpilase taseme vabaliikme jaoks). Tabelite tõlgendus on sarnane eespool antud seletustele, seepärast toome esile üksnes uued momendid, kui neid on.

Tabelist 3.1 näeme, et jah, läbisaamine õpetajatega on hinde statistiline prognoositegur.  Iga punkt õpetajaga harvema halva läbisaamise poole tõstab hinnet keskmiselt 0,12 punkti (tabel 3.2). Keskmise läbisaamise korral (tsentreeritud läbisaamise tunnus on 0) tuleb prognostiline hindetase 3,02.

 Jääkhajuvus õpilase tasemel on 0,39 (tabel 3.3). Mudeli vabaliikme dispersioon on statistiliselt oluline väga väikese olulisuse tõenäosusega, mis tähendab, et üks ja sama hinde vabaliige ei sobi ka selle mudeli puhul kaugeltki mitte kõikidele koolidele. Näeme ka seda, et õpetajatega läbisaamise tunnuse regressioonikordaja varieerub jääkdispersiooni UN(2,2) arvestades küllaltki ja seejuures positiivselt korreleerudes vabaliikmega. See tähendab, mida madalam hindetase (vabaliige), seda keskmiselt vähem oleneb hinne läbisaamisest õpetajaga (regressioonikordaja) – hinde variatiivsus on miinimumiga piiratud.

Nägime tabelist 3.2, et läbisaamine õpetajaga mõjutab hinnet keskmiselt regressioonikordajaga 0,12, mille  usaldusvahemik usaldusnivool 95% on 0,09 kuni 0,15. Lisame veel ühe viisi regressioonikordaja tõenäosuslikuks iseloomustamiseks, mis toetub sellele, et kordajat ennast vaatleme juhuslikuna. Tabelist 3.3 selgus, et selle regressioonikordaja prognoosimudeli vea dispersioon on 0,0079, standardhälve seega 0,09 ringis. Arvestades, et regressioonikordaja jaotub meie eeldustel normaaljaotuse kohaselt, võiksime niisiis öelda, et ligikaudu tõenäosusega 95% on õpetajatega läbisaamise regressioonikordaja väärtusi oodata piirides 0,12 – 1,96∙0,09 = -0,06 kuni 0,12 + 1,96∙0,09 = 0,30. Toetusime siin normaaljaotuse omadusele standardhälbe kaudu: kahe standardhälbe ulatuses on ligikaudu 95% väärtustest. Ühe standardhälbe kaugusel keskmisest ehk 0,03 kuni 0,21 on prognostiliselt umbes 2/3 regressioonikordajatest, kui toetuda meie mudelile.

Mudeli sobitusastme mõõdud tabelis 3.4 võtame teadmiseks, et neid võrrelda järgmise mudeli, mudeli 4 sobitusastmega, kus püüame eespool selgunud vabaliikme ja regressioonikordajate muutlikkust seletada hoiaku kaudu edasiõppimise suhtes (analoogia mudeliga 2.

Lisame mudelisse 3 regressioonikordajate kooli tasemel ilmnenud variatiivsuse seletuseks edasiõppimise tõepära tunnuse. See osutub statistiliselt oluliseks mõjuteguriks olulisuse tõenäosusega alla 0,0005 (tabel 4.1) nagu ka läbisaamine õpetajatega peamõjuna. Õpilase ja kooli taseme tunnuste interaktsioonitegur (läbisaamine õpetajatega ja edasiõppimise tõepära) on samuti statistiliselt oluline olulisuse tõenäosusega 0,016 (siiski selle korral vähim F-suhe – vabadusastmed lähedased, võime ligikaudu võrrelda).

Tabelist 4.2  selgub lähemalt, kui tugev on koolikonteksti arvestades kommunikatiivsete oskuste mõju hindele. Kui kool on keskmise edasiõppimise tõepäraga, siis tõstab hea läbisaamine õpetajaga hinnet keskmiselt 0,117 võrra. Õpilasel, kel on õpetajaga läbisaamine keskmisel tasemel, tõstab kooli edasiõppimise taseme tõus ühiku võrra keskmist hinnet 0,377 võrra. Kui võrrelda üht kooli teisega, milles edasiõppimise tõepära on ühiku võrra kõrgem, siis on selles teises vahe kahe õpilase keskmisel hindel 0,071 võrra suurem kui esimeses, kui nende õpilaste õpetajatega läbisaamine erineb ühiku võrra. Edasiõppimisele enammotiveeritud koolis kahandab õpetajatega halb läbisaamine hinnet keskmiselt pisut tugevamalt kui vähemmotiveeritud koolis. Miks on see nii, selle üle arutlemiseks tuleks väljuda statistilistest raamidest, milleks siinkohal ei ole ruumi.

Osutub, et koolikonteksti arvestamisega ei õnnestunud statistiliselt ära seletada õpetajaga läbisaamise mõju variatiivsust koolide lõikes. Niihästi hinde mudeli vabaliikme kui ka õpetajatega läbisaamise tunnuse regressioonikordaja prognoosivea dispersioon jääb statistiliselt oluliseks vastavalt olulisuse tõenäosustega 0,005 ja 0,034 (tabeli 4.3 liikmed UN(1,1) ja UN(2,2)). Küll aga „kadus“ kovariatsioon vabaliikme ja regressioonikordaja vahel (liige UN(2,1)). Õpetajatega läbisaamise ja hinde vaheline seos on nähtavasti delikaatne ja peen, mida niisama lihtsalt ära ei seleta.

Mudeli 4 sobitusaste on parem kui mudelis 3 (tabel 4.4). Protsentuaalselt ei ole muutus suur, aga siiski sobitusastme suurenemise suunas.

Joonisel 6  on kujutatud vaadeldava mudeli 4 kohaseid prognoosijääke normaaljaotuse suhtes tehtud tõenäosusgraafiku alusel (ülal) ja histogrammina (all). Näeme väga harvu suuri jääke ja jääkide jaotuse lahknevus normaaljaotusest ei ole suur. Olukord on selline, nagu peaks olema.

Koostame nüüd mudeli, mis on hea sobitusastme arvestuse alus kõigi võimalike mudelite puhul – ainult vabaliiget sisaldava hinde prognoosimudeli, kusjuures ka vabaliikme variatiivsust väljendava mudeli puhul ei kasuta ühtki seletavat tunnust. Üldistes tähistustes on tegemist järgmise mudeliga:

Fikseeritud osa koosneb ainult vabaliikmest (üldkeskmine hinne) ja juhuslik osa kahe avaldise vealiikmete summast.

Tabelist 5.1 ei selgu muud kui see, et üldkeskmine hinne on olulisuse tõenäosusega alla 0,0005 statistiliselt erinev nullist. Tabelist 5.2näeme, et üldkeskmine on arvuliselt 3,02 usaldusvahemikuga 2,95 kuni 3,09 usaldusnivool 95%. Tabelis 5.3  on esitatud veakomponentide dispersioonid koos komponentide nulliga võrdumise testide ja usaldusvahemikega. Selline mudel annab võimaluse hinnata, kui tugev on tegelikult tasemerühmade siseselt indiviididevaheline seos, mida võiks pidada üheks peamiseks mitmetasemelise analüüsi kasutamise kriteeriumiks. See nn rühmasisene korrelatsioonikordaja (i.k. intraclass correlation coefficient, ICC) leitakse dispersioonide suhtena: teise taseme vea u_0j dispersioon jagatud indiviidi taseme vea u_0j ja teise taseme vea r_ij dispersioonide summaga. Kui kordaja võrduks arvuga 1, oleks kogu sõltuva tunnuse variatiivsus taandatav tasemerühmade erinevusele ja tasemerühma sees valitseks ühetaolisus (”seos”). Vastupidi, kui see kordaja on nullilähedane, siis ei ole mõtet sõltuva tunnuse variatiivsuse seletusi otsida tasemerühmade kaudu ja võiksime vabalt piirduda ühetasemelise analüüsiga. Kust läheb suure ja väikese ICC piir, on raske üheselt öelda ja see on pigem andmete iseloomust ja uurimiskogemusest olenev suhteline määratlus.

Meie näites erinevad mõlemad hinde prognoosi veakomponendid – nii õpilase taseme dispersioon kui ka koolide taseme dispersioon – statistiliselt oluliselt nullist olulisuse tõenaäosusega alla 0,0005. Summaarne vea dispersioon on 0,412 + 0,059 = 0,471. Koolidevahelistest erinevustest tingitud vealiikme u_0j dispersioon 0,059 moodustab kogudispersioonist 0,125 = 0,059 / 0,471. Kahtlemata on kahetasemeline käsitlus vaeva väärt – enam kui kümnendiku mudeli vea muutlikkusest saame kirjutada koolidevaheliste erinevuste arvele, ICC = 12,5%. Mõjuteguriteta mudeli sobitusaste andmetega on ootuspäraselt palju kehvem kui mis tahes eelnevas mudelis (tabel 5.4 ).

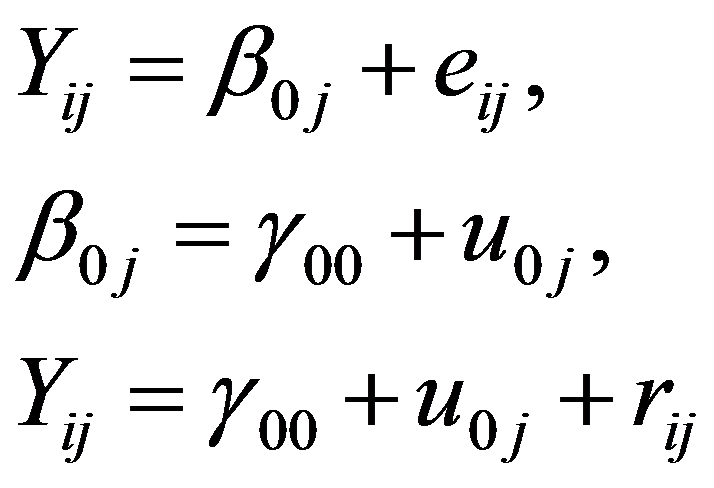
Vaatleme lõpuks, kui suure sobitusastme paranemise võrreldes lakoonilisima mudeliga 5 saavutaksime mudelis, millesse on kaasatud kõik kolm eespool vaadeldud tunnust: õpilase sugu, läbisaamine õpetajatega ja koolis valitsev hoiak edasiõppimise suhtes (edasiõppimise tõepära). Samuti pakub huvi, kuivõrd stabiilsed on regressioonikordajad, kui kogu meie (kahtlemata väga napp) info korraga mudelisse kaasata. Et soovime arvestada kooli konteksti, siis lülitame mudelisse ka interaktsioonitegurid esimese ja teise, õpilase ja kooli taseme tunnuste vahel.

Ühtlasi anname selle mudeli puhul ka ideid, kuidas esitleda mitmetasemelise analüüsi tulemusi. Üldine reegel on: sõltuvalt auditooriumist ja regressioonimudeli esitlusviisi järgides (http://samm.ut.ee/regressioonanalyys). Tähtsaid üksikasju nimetame allpool iga tabeli juures.

Mõjutegurite statistilise olulisuse suhtes uudist esile ei tule (tabel 6.1 ) – kõik mudeli liikmed on statistiliselt olulised vähemalt olulisuse nivool 4%, välja arvatud sootunnuse kontekstuaalne eripära (soo ja edasiõppimise tõepära interaktsioon). Kokkuvõtliku mudeli regressioonikordajad ei paku samuti üllatusi (tabel 6.2). Regressioonikordajate märgid on samad, mis eespool olnud mudeleis, statistilise olulisuse tõenäosused samuti ja kordajad on arvuliselt üksnes pisut muutunud. Tõlgendus ja järeldused ei muutu. Esitlus: tabelis oleva info mõjutegurite statistilise olulisuse kohta võib kirjutada teksti sisse. Laiale auditooriumile nimetada tegurite mõju suund ja tähendus, asjatundjatele anda regressioonikordajad (koos usaldusvahemikuga) ja/või osutada regressioonikordajad koos olulisuse tõenäosustega. Kui esitatakse võrdlevalt mitu mudelit, siis tuleks püüda neid koondada ühisesse tabelisse. Tabelisse võib lisada täiendavad read, millel näidata sobitusastme mõõdud.

Kokkuvõtliku tabeli dispersioonikomponentide statistiline olulisus ühtib eelnevates mudelites leituga (tabel 6.3): hinnete variatiivsus õpilase tasemel jääb statistiliselt oluliseks,  vabaliikme variatiivsus jääb kooli tasemel ammendavalt seletamata ja samuti õpetajatega läbisaamise regressioonikordaja muutlikkus. Kovariatsioonid regressioonikordajate ja vabaliikme vahel (liikmed UN(2,1) ja UN(3,1)) olid ka eespool statistiliselt mitteolulised ja selliseks osutub ka sootunnuse ja õpetajatega läbisaamise tunnuse vaheline kovariatsioon (liige UN(3,2)).

Tabelisse 6.4  on koondatud kõigi vaadeldud mudelite sobitusastmete kordajad. Nende võrdlemisel tasub silmas pidada, et tõepärafunktsioonide erinevust saab kriteeriumina kasutada üksnes üksteises sisalduvate (i.k. nested) mudelite võrdlemisel. Ühise võrdluse lähtealusena sobib kõigile muidugi mõjuteguriteta mudel 5.  Esitlus: võib-olla piisab sobitusastme kirjeldusest teksti sees.  Sobitusastme mõõdud tähendavad midagi võrdlevalt, mitme mudeli kõrvutamisel. Selles ülesandes võiks esitleda nt mudeli 5 ja mingi teise mudeli mõõdikud. Võib-olla piisab ainult kordajate AIC ja BIC esitamisest.