Cronbachi kordaja

Sotsiaalse nähtuse kirjeldamiseks ei piisa tavaliselt ühest või vähesest arvust tunnustest, vaid kasutusele võetakse palju tunnuseid korraga ja käsitlus on enamjaolt mitmemõõtmeline. Veel enam, ka üksikomaduse esiletoomiseks kasutatakse vastava mõiste operatsionaliseerimisel harva ühtainust näitajat, vaid vaadeldakse seda mõistet peegeldavat üksiktunnuste rühma, mida kokkuvõtvalt võiks matemaatilist analoogiat kasutades nimetada ka tunnusvektoriks. Nii näiteks vaatleme allpool inimeste poliitilise usalduse indikaatoritena usaldust seitsme institutsiooni suhtes, kasutades Euroopa sotsiaaluuringu sellekohaseid andmeid (European Social Survey …). Psühhomeetrias nimetatakse ühe omaduse või objekti indikaatorite kogumit skaalaks ja selle komponente „ühikuteks“ (ik item). Allpool kasutame väljendit „tunnusrühm“ ja selle komponente nimetame üksiktunnusteks.

Tunnusrühma kasutamise loogikat teatud omaduse (nt rahuloluaste, teadmiste tase) mõõtmiseks illustreerib joonisel 1 kujutatud mõõtmismudel: tõeline väärtus T peegeldub üksiktunnustes Y₁, Y₂, …, Y_K vastavalt vigadega e₁, e₂, …, e_K ja tõelise väärtuse hinnanguna kasutatakse üksiktunnuste kaalutud summat vastavalt kaaludega b₁, b₂, …, b_K. Vigade kohta on loomulik eeldada, et need on keskmiselt võrdsed nulliga (iga üksiktunnus mõõdab keskmiselt õigesti), üksteisest sõltumatud (iga üksiktunnus „eksib“ teistest sõltumatult) ja ei sõltu ka tõelisest väärtusest (mõõtmine on mõõdetava suuruse suhtes ühtlaselt täpne).

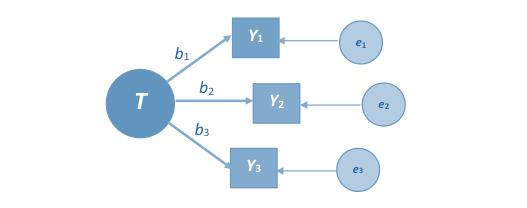
Vaatleme lähemalt seda skeemi poliitilise usalduse näitel. Euroopa sotsiaaluuringus mõõdetakse sotsiaalset usaldust usalduse kaudu maa parlamendi, poliitikute, poliitiliste parteide, politsei ja õigussüsteemi vastu ning usalduse kaudu ÜRO ja Euroopa Parlamendi vastu (esitati vastavalt küsimused „Kuivõrd usaldate Riigikogu?“, „Kuivõrd usaldate poliitikuid?“ jne). Need on skeemil 1 tunnused Y₁, Y₂, …, mille variatiivsus on meie mudeli kohaselt olulises ja tunnuseti mitte tingimata ühetaolises ulatuses (kordajad b₁, b₂, …) määratud poliitilise usalduse T poolt. Teatud osa variatiivsusest kujundab mudeli viga e₁, e₂, …, sh juhuslik mõõtmisviga (nt küsitletu hetkeseisundist olenev).

Mõõtmismudeli vigade headele omadustele vaatamata jääb vastuseta küsimus, kui asjakohane on selline tunnusrühm vaadeldava omaduse uurimisel: kas mõõdame seda, mida arvame mõõtvat (valiidsus, ik validity) ja kui töökindlalt (reliaablus, ik reliability). Viimane vaatenurk viibki meid Cronbachi kordaja juurde.

Reliaablus on mitmetahuline ja keeruline mõõtmisteoreetiline mõiste. Reliaabluse astet konkreetse mõõdiku (testi, tunnusrühma) puhul väljendab lõppkokkuvõttes see, kui suur on tõelise väärtuse statistilise variatiivsuse ja mõõdiku kaudu saadud väärtuse (tõeline väärtus + viga) statistilise variatiivsuse suhe. Mida töökindlam mõõtmine, seda lähemal on see suhe arvule 1.

Reliaablust käsitletakse erinevatest vaatenurkadest ja erineva tähendusvarjundiga: katse- või vaatlustulemuste korratavus (st tulemuste püsivus kordamisel), mõõdiku seesmine kooskõla (järjekindlus, konsistentsus). Erinevad on ka vahendid reliaabluse kindlakstegemisel: seos erinevate indiviidide/ekspertide mõõtmiste vahel (ik inter-rater reliability), seos kordusmõõtmiste vahel (ik test-retest reliability), seos samal eesmärgil loodud eri testide vahel (ik parallel-form reliability), seos testi eri elementide vahel (ik internal consistency reliability). Viimati nimetatu − seesmise konsistentsuse reliaabluse − määra üks mõõdikutest ongi Cronbachi kordaja ehk Cronbachi alfa-kordaja traditsioonilise tähistuse α järgi. Konsistentsuse mõte võib uurimisprobleemist olenevalt erineda: järjekindel, ajas püsiv, ühetaoline, tihe, kooskõlaline, ühtne mõõtmine. Seesmise konsistentsuse mõttes reliaablust võiks nimetada ka sisereliaabluseks. Reliaabluse teemal üldisemalt siinkohal rohkem ei peatu (vt nt Elmes jt 2013, lk 177, 425; Types of Reliability …).

Lee Joseph Cronbach arendas oma reliaabluse kontseptsiooni välja G. F. Kuderi ja M. W. Richardsoni töödele toetudes ja pakkus 1951. aastal ilmunud alfa-kordaja tunnusrühma seesmise konsistentsuse reliaabluse astme hindamiseks. Cronbachi kordaja on saavutanud praktikas tohutu populaarsuse ja leiab sageli ka mõõdutundetut rakendamist. Kordaja kasutamise eelduseks on tunnusrühma aditiivsus uuritava omaduse mõõtmisel, st komponendid liituvad ja puudub üksiktunnuste interaktsioon. Eelduseks on ka see, et tunnusrühma taga on üks omadus (konstrukt), ja kordaja võimaldab hinnata, kui suur on tunnusrühma reliaablus sellisel eeldusel (vt nt Tavakol ja Dennick 2011). Üksiktunnused peavad olema positiivselt korreleeritud (vajadusel muuta mõõtmistelje suund vastupidiseks) ja need liituvad tulemuseks võrdsete kaaludega (tulemus on üksiktunnuste summa: b₁ = b₂ = … = b_K). Sellistel eeldustel Cronbachi kordaja α leitakse valemist (üks võimalikke kujusid)

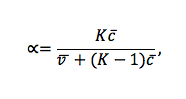
kus c  on üksiktunnuste vaheliste kovariatsioonikordajate keskmine, v üksiktunnuste keskmine dispersioon ja K tunnuste arv tunnusplokis (skaalas). Standardiseeritud Cronbachi kordaja α_st arvutus on analoogiline. Kui r on tunnusploki üksiktunnuste vaheliste Pearsoni korrelatsioonikordajate keskmine, siis

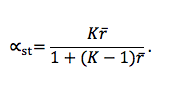
Otsuse selle kohta, kas kasutada standardimata (kovariatsioonidel põhinevat) kordajat või standarditud (korrelatsioonimaatriksil  põhinevat) kordajat, teeb uurija ise selle põhjal, kas omaduse mõõtmiseks kasutatakse esialgsete tunnuste summat või standarditud tunnuste summat (nt tunnuste erisuguste standardhälvete korral). Esimesele juhule vastab α, teisele α_st.

Arvutusvalemeist tuleneb, et Cronbachi kordaja väärtust mõjutab tunnustevaheline üldine kovariatsiooni/korrelatsioonseose tugevus, mis on väga loomulik, sest püüame hinnata tunnusrühma seesmist tähenduslikku kooskõla.

Siin on kohane tähelepanu juhtida seesmise järjepidevuse reliaabluse teistele kordajatele Cronbachi kordaja kõrval (vt nt ka Eisinga jt 2013). Kui üksiktunnused on erineva raskusastmega, siis võib tekkida soov lülitada neid võrdsustamiseks mõõtmismudelisse teatud kaaludega ja see tähendab alfa-kordaja eelduse rikkumist. Mittevõrdsete kaaludega summa on loomulikum kui summa (meenutame kasvõi faktorlaadungeid faktoranalüüsis või peakomponentide analüüsis). Sellise juhu jaoks pakkus ühe lahenduse Karl Jöreskog 1971. aastal ja hiljem tuli veel teisigi eeskirju, mis arvestavad reliaabluse hindamisel üksikküsimuste kaalusid. Spearmani-Browni valem reliaabluse mõõtmiseks seob testi pikkuse (st üksiktunnuste arvu) reliaabluse määraga. Kui üksiktunnused on dihhotoomsed (0 ja 1), siis taandub Cronbachi kordaja Kuderi-Richardsoni valemiks, mis on tuntud KR-20 nime all (nende autorite töödes oli hulk erinevaid reliaabluse arvutuseeskirju).

Mida järeldada kõrgest reliaablusest? Eeldades, et tunnusrühm mõõdab üht konstrukti, saame öelda, et mõõtmine on küllalt töökindel. See tähendab, kui meenutada mõõtmismudeli skeemi joonisel 1, et tõeline omadus (nt poliitilise usalduse määr) on üksikküsimustega kooskõlaliselt tabatud ja summaarse mõõtmistulemuse hajuvus on lähedane omaduse tõelisele hajuvusele vaadeldavas kogumis.

Kas Cronbachi kordaja võib tulla ka negatiivne? Jah, aga see ei kõnele õnnestunult koostatud mõõdikust. Cronbachi kordaja eeskirjale tuginedes saab lihtsalt näidata (vt nt Nichols), et kordaja tuleb negatiivne, kui üksiktunnuste keskmine kovariatsioon tuleb negatiivne. Selle taga võib olla see, et ununes skaalade suuna sisuline ühtlustamine, et valimi väiksuse tõttu on tegelikult positiivse kovariatsiooni hinnang valimi alusel negatiivne, või esineb olukord, kus tunnusrühm ei olegi seesmiselt konsistentne ning vajab muutmist, sest ei toimi uuritava omaduse mõõtmisel kooskõlaliselt.

Nimetame lõpuks kokkuvõtlikult, milliste tunnuste puhul sobib uurida tunnusploki sisemist kooskõla Cronbachi kordaja abil. Tunnuse tüübist lähtudes sobivad arvulised tunnused (või arvulisena tõlgendatavad tunnused), sest kesksel kohal on kovariatsiooni uurimine. Nominaaltunnuseid tuleks käsitleda teisendatuna dihhotoomseteks indikaatoriteks. Andmete lünklikkusest ülesaamiseks, kui puuduvaid väärtusi on vähe, võib soovitada lünklike indiviidide paarikaupa elimineerimist korrelatsioonimaatriksi koostamisel.

Cronbachi kordaja arvutus on kättesaadav enamikes laiema levikuga programmipakettides üsna sarnasel moel. Kui käepärast on ainult Excel (andmeanalüüsi mooduliga Data Analysis korrelatsioonimaatriksi arvutamiseks), on seegi lahendus, sest arvutusvalem, mida ise kirjutada, ei ole keeruline.

Cronbachi kordaja arvulise väärtuse leidmise kõrval on programmipakettides realiseeritud veel mitmeid kõrvaltegevusi tunnusrühma analüüsimiseks: aditiivsuse testimine, detailse kirjeldava statistika esiletoomine. Vaatleme neist põhiosa paketi SPSS abil lahendatud näites (vt ka What does Cronbachs alpha mean …).

Näites kasutame Euroopa sotsiaaluuringu 2018. aasta uurimisvooru andmeid Eesti kohta (vt European Social Survey …) ja hindame poliitilise usalduse tunnusrühma sisest reliaablust. Tunnusrühmaga koguti andmeid vastusena küsimusele „Kuivõrd Te usaldate järgmisi institutsioone?“ Riigikogu, Eesti õigussüsteemi, politsei, poliitikute, poliitiliste parteide ja erakondade kohta ning Euroopa Parlamendi ja Ühinenud Rahvaste Organisatsiooni kohta. Vastati skaalal 0 (ei usalda üldse) kuni 10 (usaldan täielikult). Ülesanne on hinnata poliitilise usalduse tunnusrühma reliaablust sisemise kooskõla mõttes. Tabelis 1 on näidatud poliitilise usalduse üksiktunnuste keskmised ja standardhälbed ning tunnuste omavahelised Pearsoni korrelatsioonikordajad.

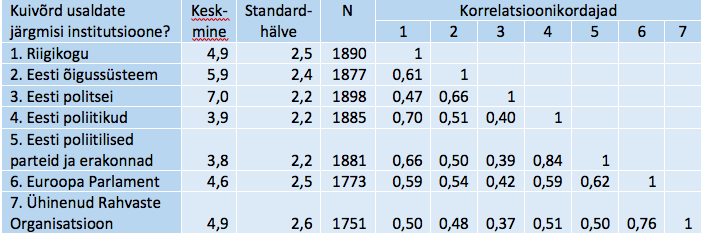
Keskmine korrelatsioonikordaja on 0,55 standardhälbega 0,12 ja see annab otseselt valemi alusel arvutades standarditud Cronbachi kordaja α_st väärtuse 0,897:0,897 = 7*0,554 / (1+ 6*0,554). Küsitletud indiviidide üldarv on 1904 ja, nagu näha, on tunnustes lünki, eriti kahel viimasel üksiktunnusel. Korrelatsioonimaatriksi paarisvalimite maht kõigub 1727 ja 1890 vahel ja lünkadeta indiviide selles tunnusrühmas on 1709. Cronbachi kordaja on lähedal arvule 1 ja tunnusrühma vastuste sisemise kooskõla mõttes reliaablus seega kõrge, kui vaadelda kasutatud tunnuseid poliitilise usalduse mõõdikutena. Siiski ei ole mõistlik kehtestada absoluutseid piire reliaabluse liigitamiseks, kuigi praktikas sageli seda tehakse (nt 0,6 või 0,7 kui piisava reliaabluse alampiir). Sisukam on kordaja väärtuste võrdlus omavahel, nt tunnusrühma sisulisel muutmisel.

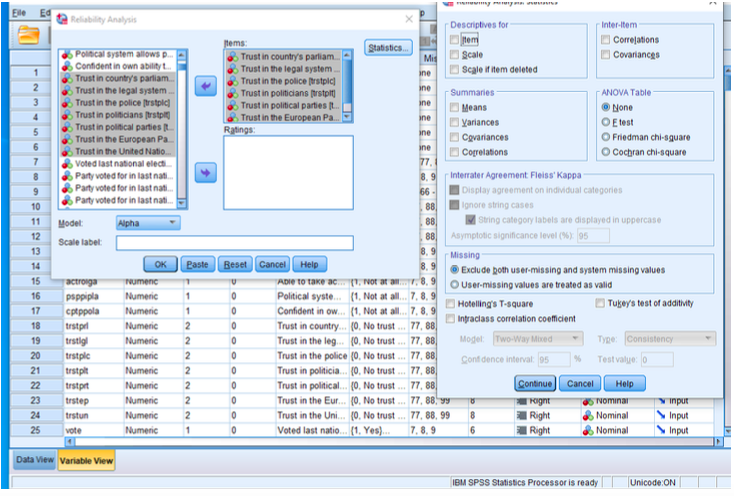
Paketi SPSS käsud menüü kaudu lahendamisel on järgmised (vt ka Reliability Analysis …).

Käsureaga Analyze – Scale – Reliability Analysis avatakse reliaablusanalüüsi moodul, mille põhiaknas (joonis 2) tuleb:

• kanda uuritava tunnusrühma tunnuste nimed väljale Items,
• teha valikud sildi Model all,
• teha valikud sildi Statistics all,
• soovi korral omistada väljal Scale label uuritavale tunnusrühmale (skaalale) nimi.

Lisame, et välja Ratings kasutada tunnuste valikuks siis, kui vaadeldava mooduliga soovitakse arvutada Fleissi kapa-kordajat ekspertide kooskõla uurimiseks.

Sildi Model valikud määravad reliaabluse hindamise viisi:

 Alpha – Cronbachi kordaja arvutamine ja analüüs tunnustevahelise keskmise korrelatsiooni alusel; see on põhiline valik, kui ei ole tegemist reliaabluse detailse analüüsiga kitsamalt mõne psühhomeetrilise probleemi lahendamisel või uue testi väljatöötamise käigus, mil võiksid kasuks olla ka mudeli ülejäänud variandid;

Split-half – tunnusrühm poolitatakse ja reliaablust uuritakse kahe poole tunnuste omavahelist korrelatsiooni kasutades, Guttman – hinnatakse reliaabluse alampiiri (Louis Guttman pakkus mitmeid hinnanguid selleks), Parallel – eeldatakse, et tunnused on sama hajuvusega ja sama hajuvusega on ka mõõtmismudeli vead (joonis 1); Strict parallel – eeldatakse, et tunnused on sama keskmisega, sama hajuvusega ja sama hajuvusega on ka mõõtmismudeli vead.

Sildi Statistics valikud on järgmised (joonis 2).

Väljal Descriptives for on võimalik valida põhilise kokkuvõtliku statistika esiletoomine:

Item – keskmiste ja standardhälvete arvutus iga üksiktunnuse jaoks (kasutatakse terve tunnusrühma seisukohalt lünkadeta andmestikku);

Scale – keskmiste ja standardhälvete arvutus tunnusrühma summa jaoks;

Scale if item deleted – kõrvutatakse kogu tunnusrühma (skaala) keskmisi ja standardhälbeid ja Cronbachi kordajaid, mis on leitud olukorras, kus konkreetne tunnus on rühmast välja jäetud; tuuakse esile konkreetse tunnuse ja ülejäänute mitmene korrelatsioonikordaja.

Väljal Summaries on võimalik esile tuua tunnusrühma kooskõlalisuse iseloomustamiseks üksiktunnuste kokkuvõtlike suuruste statistika:

Means – tunnusrühma üksiktunnuste keskmiste keskmine, miinimum ja maksimum, haare, suurima ja vähima keskmise suhe keskmise taseme varieeruvuse hindamiseks;

Variances – tunnusrühma üksiktunnuste keskmiste keskmine, miinimum ja maksimum, haare, suurima ja vähim tunnusrühma üksiktunnuste dispersioonide keskmine, miinimum ja maksimum, haare, suurima ja vähima dispersiooni suhe hajuvusastme varieeruvuse hindamiseks;

Covariances – tunnusrühma üksiktunnuste keskmiste keskmine, miinimum ja maksimum, haare, suurima ja vähim tunnusrühma üksiktunnuste vaheliste kovariatsioonikordajate keskmine, miinimum ja maksimum, haare, suurima ja vähima kovariatsioonikordaja suhe koosvarieeruvuse määra varieeruvuse hindamiseks;

Correlations – tunnusrühma üksiktunnuste keskmiste keskmine, miinimum ja maksimum, haare, suurima ja vähim tunnusrühma üksiktunnuste vaheliste korrelatsioonikordajate keskmine, miinimum ja maksimum, haare, suurima ja vähima korrelatsioonikordaja suhe korrelatsioonseose varieeruvuse hindamiseks.

Välja Inter-item kaudu on võimalik esile tuua üksiktunnuste vaheline korrelatsioonimaatriks (valik Correlations) ja/või kovariatsioonimaatriks (Covariances).

Väli ANOVA Table – dispersioonanalüüs üksiktunnuste keskmiste võrdumise hüpoteesi testimiseks – võib kas ära jätta (valik None) või kujundada seda kolme liiki statistikute kasutamise kaudu:

F-test – kordusmõõtmistega dispersioonanalüüsi F-statistikul põhinev analüüs,

Friedman chi-square – järjestustunnuste korral kasutatakse F-statistiku analoogina Friedmani teststatistikut,

Cochran chi-square – dihhotoomsete tunnuste korral kasutatakse Cochrani statistikut Q F-statistiku analoogina.

Analoogiliselt dispersioonanalüüsile on ka Hotellingi T-testi eesmärgiks hüpoteesi kontrollimine üksiktunnuste keskmiste võrdsuse kohta (vajadusel lisada linnuke ruudu Hotelling’s T-square ette).

Tukey aditiivsuse test võimaldab kontrollida eeldust, et summaarne tulemus avaldub üksiktunnuste liitumisel ega sisalda nende interaktsioonikomponente (valik Tukey’s test of additivity käivitab selle analüüsi).

Klassisisese korrelatsioonikordaja (valik Intraclass correlation coefficient) mõtteks siinkohal on näidata tunnusrühma kooskõla indiviidide kaupa, indiviidi andmete reas. Arvutusi saab varieerida, et võrrelda eri põhimõtteil saadud tulemusi, kuid parim viis vastavad valikud enesele selgeks teha tekib päris oma ülesannet kasutades.

Nende kohtade jaoks, kus reliaablusanalüüsis tehakse statistilisi otsustusi, saab ette anda soovitava usaldusnivoo. Testide jaoks, mis siin analüüsis on, saab kirjeldada ka nullhüpoteesi kohase väärtuse (vaikimisi 0).

Osa Interrater Agreement Fleiss’ kappa kasutatakse siis, kui eesmärgiks on Fleissi kordaja arvutus ekspertide-hindajate hinnangute koosküla uurimiseks. 

Rakendasime äsja kirjeldatud valikuid institutsioonide usaldushinnanguist koosneva tunnusrühma reliaabluse analüüsimisel poliitilise usalduse näites. Põhilised tulemuste osad on esile toodud lahenduse kordamise huvides paketi SPSS tabelite  vormis, mida lõppvormistuses tuleks kindlasti muuta kompaktsemaks. Tekstis on järgnevatel tabelitel erinumeratsioon SPSS_1, SPSS_2 jne, et oleks kergem jälgida arvutiväljundit oma ülesandes ja ise näidet kaasa lahendades (Euroopa sotsiaaluuringu andmestikud on vabakasutuses ja kättesaadavad uuringu eespool viidatud kodulehel). Iga tabeli järele on lisatud väike kommentaar.

Listwise deletion based on all variables in the procedure. – Andmelünkade väljajätmine tunnuste loetelu alusel.

Tabelist SPSS_1 on näha kümnendiku jagu kadu andmelünkade tõttu. Lünklikkuse laadi tuleks kindlasti uurida, kas see on juhuslik, sest tunnustele vastamine-mittevastamine võib oleneda informeeritusest ja kindlasti ka huvist poliitiliste küsimuste vastu.

Tabelist SPSS_2 näeme juba eestpoolt tuttavat arvu, kui rakendasime arvutustes vahetult valemit. Formaalselt võttes on tunnusrühma sisemine kooskõla Cronbachi kordaja alusel väga suur. Andmete standardimine kordajat märkimisväärselt ei muuda (tunnused on küllaltki ühetaolise hajuvusastmega).

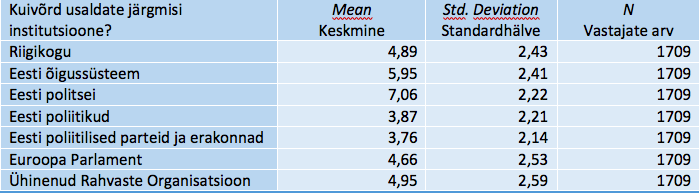
Tabelist SPSS_3 jääb silma suur keskmine usaldus politsei vastu, poliitikute ja poliitiliste parteide väike usaldus ja nendest pea punkti võrra kõrgem Riigikogu usaldus. Tähelepanu äratab ka standardhälve, mis on välisinstitutsioonide korral suurem kui teiste hinnangute puhul. Need andmed kõigutavad pisut Cronbachi kordaja alusel tekkinud veendumust, et poliitiline usaldus on ühtne ja üheainsa näitajana esitatav (nagu eeldatakse kordaja kasutamisel). Lisame veel, et keskmised ja standardhälbed erinevad pisut tabelis 1 tooduist, mille taga on lünklike indiviidide erisugune käsitlus: siin tabelis tunnuste loetelu järgi ja tabelis 1 üksiktunnuste kaupa.

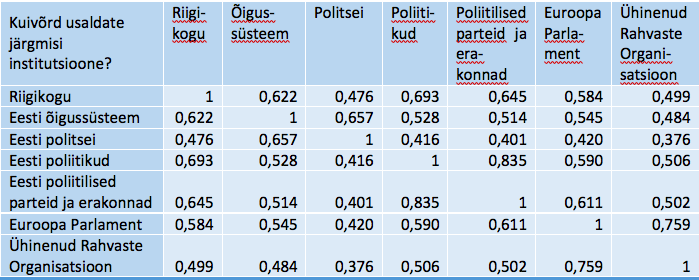
Ligilähedaselt kõneldes peegeldab Cronbachi kordaja tunnustevahelist keskmist korrelatsiooni. Seega otsime korrelatsioonimaatriksit vaadeldes vastust küsimusele, kui tugev ja kui ühtlane on tugevuselt korrelatsioonseos meie tunnusrühmas. Hea tähelepanek tabelist SPSS_4 on see, et ei ole nõrgalt seotud tunnuseid (nõrgim seos kordajaga 0,38 ÜRO ja Eesti politsei usaldushinnangute vahel) ja samuti mitte liiga tugevalt korreleerituid (tugevaim seos 0,84 poliitikute ja parteide usaldushinnangute vahel, 70% ulatuses vastastikku kirjeldatud variatiivsus). Ühtlast seosetugevust kinnitada ei tahaks: korrelatsioonikordajad muutuvad piirides 0,38 kuni 0,84.

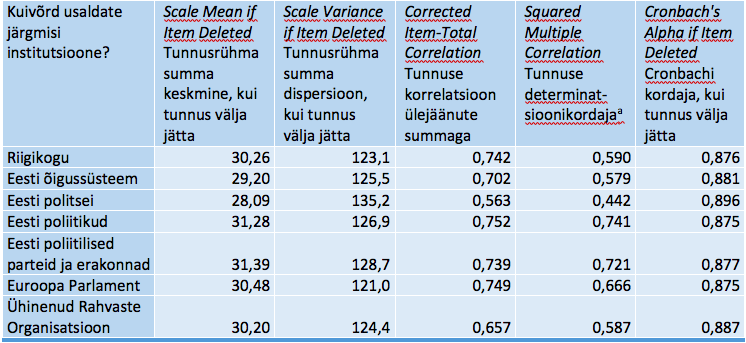
^a Tunnuse determinatsioonikordaja tunnusrühmas on tunnuse mitmese korrelatsioonikordaja ruut.

Tabeli SPSS_5 mõte on kõrvutada iga tunnust ülejäänutega, et selgitada, kuivõrd tugevaks mittekooskõla allikaks (mustaks lambaks või valgeks vareseks) on see tunnus ülejäänute seas. Kui tunnused on võrreldavad uuritava omaduse peegeldamisel, siis muutub tunnusrühma summa tunnuste ühekaupa väljajätmisel ühevõrra. Praegu see nii ei ole – summa kukub märgatavalt, kui välja jääb politsei usaldushinne (28,09). Näeme ka, et politsei usaldushinne on teiste summaga kõige nõrgemalt seotud (0,442). Samuti on selle tunnuse determinatsioonikordaja ülejäänute kaudu prognoosimisel madalaim. Kui politsei usaldushinnang tunnusrühmast välja jätta, siis Cronbachi kordaja ei muutu, kuid ülejäänud tunnuste väljajätmine vähendab kordajat. Tõsi küll, muutus ei ole suur. Tundub, et politsei usaldushinnangut ei ole siiski alust pidada erandlikuks selles tunnusrühmas (Cronbachi kordaja väärtus tunnuse väljajätmisel säilib), aga tabelis ilmnenud väikest eripära võiks meeles pidada küll. Kui mõne tunnuse väljajätmine suurendaks märgatavalt Cronbachi kordaja väärtust, siis oleks alust tunnusrühma puhastada selle tunnuse väljajätmise teel ja seesmist ühetaolisust seeläbi suurendada.

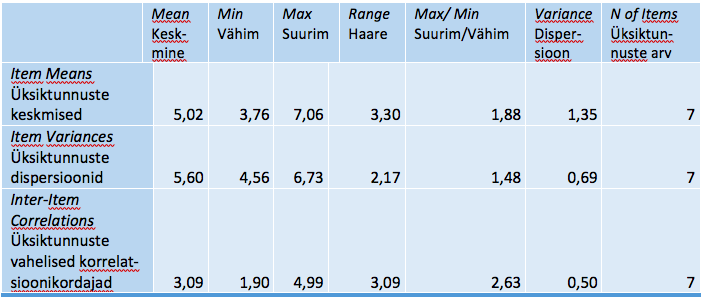
Tabelis SPSS_6 võetakse kokku see, mida nägime eespool tabeleis SPSS_3 ja SPSS_4. Üksiktunnuste üldkeskmine on 5,02 (meenutame, et hindamisskaala on 0 kuni 10), kõrgeim keskmine on 6,7 ja madalaim 3,8 ning nende suhe 1,9, st peaaegu kahekordne. Suurim dispersioon on pooleteisekordne vähim dispersioon. Tugevaim korrelatsioon on enam kui kahe ja poole kordne nõrgim korrelatsioon. Siin kordame eespoolöeldut: ei saa väita, et poliitilise usalduse mõõdiku osad on nö võrdsed tegijad ja nende summa peegeldab ühetaoliselt neid kõiki. Sellest ei oleks midagi, sest võiks kasutada ka kaalutud summat, aga Cronbachi kordaja peegeldab reliaablust juhul, kui kaalud on võrdsed. Seega näib, et peaksime oma näites järelduste tegemisel suhtuma kordajasse ettevaatlikult.

Tabelist SPSS_7 selgub, et usalduse kogumäär (tunnuste summa, skaala summaarne skoor) on keskmiselt 35,2 dispersiooniga 169. Nende arvude taustal võiks veel kord vaadelda tabelit 5, kus näidatakse, mis juhtub summaarse skooriga, kui konkreetne tunnus välja jätta (nt politsei usaldushinnang).

^a Lühend fraasist Number of degrees of freedom (vabadusastmete arv). F-statistikul on siinkohal kaks vabadusastmete arvu: ühe võrra vähendatud tunnuste arv ja indiviidide arv miinus ühe võrra vähendatud tunnuste arv.

Tabelis SPSS_8 on esitatud Hotellingi testi tulemused kontrollimaks hüpoteesi selle kohta, et tunnuste keskmised on ühetaolised. See hüpotees tuleb kummutada olulisuse tõenäosuse korral, mis on alla 0,0005. Järeldus tehakse F-jaotuse alusel vastavate vabadusastmete arvude korral.

Näite kokkuvõte

Millise kokkuvõtte võiksime nendest tulemustest teha poliitilise usalduse tunnusrühma kohta? Cronbachi kordaja osutab tugevale sisereliaablusele. Nägime aga, et tunnuste keskmised on erinevad ja sellele osutas ka Hotellingi test (samuti dispersioonanalüüs, tulemust ei ole siin ära toodud). Kui poliitilise usalduse määraks on üksiktunnuste summa, siis ei saa arvestada üksiktunnuste ühesuguse mõjuga lõpptulemusele. See tekitab mõtte uurida, kuivõrd tunnusrühm on summale toetudes üheainsa latentse näitaja peegeldus, nagu eeldatakse Cronbachi kordaja puhul. Rakendasime selle selgitamiseks faktoranalüüsi ja peakomponentide analüüsi, mis näitasid, et üheainsa konstrukti korral saab üksiktunnuseid kirjeldada mõõdukal määral (faktoranalüüs 56% ja peakomponentide analüüs 62%), kuid kaht latentset tunnust eeldades on kirjeldusaste tükk maad parem (vastavalt 64% ja 74%). Tabelist 2 (siin taas kogu teksti läbiv nummerdamine) on näha, et ühekomponendilises konstruktis on kordajad tõepoolest lähedased 0,8 ringis, välja arvatud politsei usaldushinnang. Õigussüsteemi ja politsei usaldushinnangud osutuvad teise, tõsi küll, esimesega võrreldes mitmeid kordi väiksema kirjeldusjõuga peakomponendi tuumikuks.

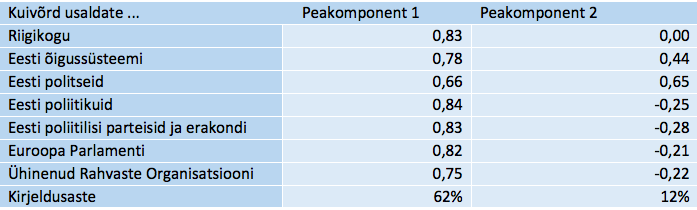
Vaadeldavas ülesandes ei ole tegemist olukorraga, kus koostatakse uut testi ja Cronbachi kordaja aitaks seejuures testiküsimusi sõeluda. Meie ülesanne oli pigem toetuse otsimine mõttele, et võiks kasutada summaarset poliitilise usalduse näitajat tunnusrühma alusel, mis on aastaid Euroopa sotsiaaluuringus olnud kasutusel ja kuulub iga kahe aasta tagant toimuva Euroopa ühiskondade monitooringu püsiküsimuste hulka. Alternatiiv oleks analüüsida erinevaid usalduse mõõtmeid eraldi või summeerida tunnuseid väiksemate rühmadena (nt usaldus poliitikute, parteide ja parlamentide suhtes). Cronbachi kordaja ei andnud väga veenvat vastust (mitme konstrukti kahtlus), kuigi arvuliselt ületas rangedki piisava reliaabluse läved. Arvatavasti võiks meie andmeis reliaabluse astet lisaks kogu tunnusrühmale kirjeldada ka veel selle alarühmades. Nii või teisiti – Cronbachi kordaja uurimine aitas süveneda poliitilise usalduse kujunemismehhanismi.

Eisinga, R., te Grotenhuis, Pelzer, B. (2013). The reliability of a two-item scale: Pearson, Cronbach or Spearman-Brown? International Journal of Public Health, 58, 637–642.

Elmes, D.G., Kantowitz, B.H., Roedinger, III, H. L. (2013). Psühholoogia uurimismeetodid. Tartu Ülikooli Kirjastus.

European Social Survey. Data and Documentation. (https://www.europeansocialsurvey.org/data/; vaadatud 30.12.2019).

Nichols, D. P. My Coefficient a is Negative! (https://stats.idre.ucla.edu/spss/library/how-negative-reliability-coefficients-can-occur/; vaadatud 21.12.2019).

IBM Knowledge Center. Reliability Analysis. (https://www.ibm.com/support/knowledgecenter/bg/SSLVMB_23.0.0/spss/base/idh_reli.html; vaadatud 30.12.2019).

Tavakol, M., Dennick, R. (2011). Making sense of Cronbach’s alpha. International Journal of Medical Education, 2, 53–55.

Research Methods Knowledge Base. Types of Reliability. https://socialresearchmethods.net/kb/reltypes.php; vaadatud 30.12.2019).

UCL, Institute for Digital Research and Education. What does Cronbach’s alpha mean?  (https://stats.idre.ucla.edu/spss/faq/what-does-cronbachs-alpha-mean/; vaadatud 30.12.2019).