Andmete kaalumine

Mida kujutab endast küsitlusandmete kaalumine? Kõige üldisemalt võiks öelda, et tegu on protseduuriga, millega korrigeeritakse uuritava kogumi iga üksikliikme mõjukust analüüsis. Vaatame ühte lihtsamat näidet selle selgitamiseks.

Eurostati andmetel varieerub inimeste osakaal, kes oskavad võõrkeeli, Euroopas riigiti märgatavalt.

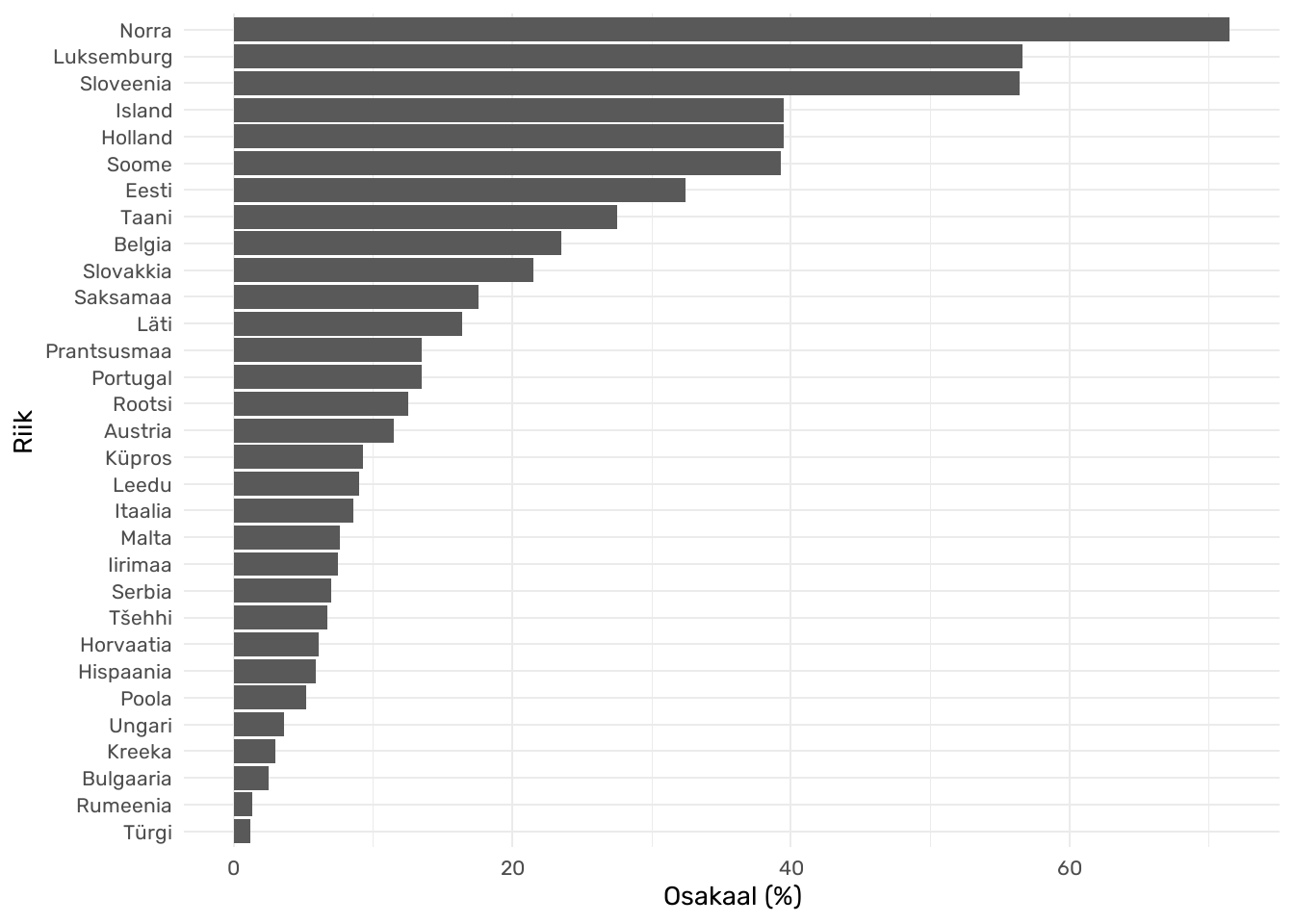
Joonis 1. Vähemalt kolme võõrkeelt oskavate elanike osakaal 18–64-aastaste vanusegrupis  2022. aastal. Allikas: Eurostat

Kui soovime teada saada, kui suur osa Euroopa elanikest (täpsemalt, uuritavate riikide elanikest) oskab vähemalt kolme võõrkeelt, kas saaksime selle arvutada joonisel 1 olevate osakaalude aritmeetilise keskmisena? Ei saaks, tulemus ei oleks täpne – selline tehe ei võtaks arvesse, et erinevates riikides on elanike arv erinev. Teisiti öeldes, käsitleksime andmeid nii, nagu igas riigis oleks (18–64-aastaste  vanusegrupis) võrdne arv elanikke. Sellisel juhul oleks osakaalude keskmine 18,6%. See ülehindab vähemalt kolme võõrkeelt oskavate inimeste osakaalu Euroopas, sest väiksemate riikide osakaalud panustavad aritmeetilisse keskmisesse ebaproportsionaalselt rohkem, kui nende elanike arv lubaks, sest väiksemates riikides on reeglina mitme võõrkeele oskajaid rohkem. Et saada teada, kui suur osa Euroopa elanikest vähemalt kolme võõrkeelt oskab, peaksime keskmise arvutamisel korrigeerima iga riigi osakaalu mõjukust vastavalt riigi elanike arvule 18–64-aastate vanusegrupis (Tabel 1). Tehniliselt ütleksimegi, et kaalume andmed läbi elanike arvuga, selle tulemusena saame kaalutud aritmeetilise keskmise.

Tabel 1. Vähemalt kolme võõrkeelt oskavate elanike osakaal koos elanike arvuga vanusegrupis 18–64 aastat 2022. aastal.

Riik	Osakaal (%)	Elanike arv
Norra	71,5	3519809
Luksemburg	56,6	447525
Sloveenia	56,4	1344499
Holland	39,5	11352758
Island	39,5	250078
Soome	39,3	3417411
Eesti	32,4	841851
Taani	27,5	3732373
Belgia	23,5	7416490
Slovakkia	21,5	3616958
Saksamaa	17,6	53193690
Läti	16,4	1184142
Prantsusmaa	13,5	42003862
Portugal	13,5	6601650
Rootsi	12,5	6494457
Austria	11,5	5941650
Küpros	9,3	609929
Leedu	9,0	1827984
Itaalia	8,6	37488934
Malta	7,6	354465
Iirimaa	7,5	3368551
Serbia	7,0	4375357
Tšehhi	6,7	6654190
Horvaatia	6,1	2441548
Hispaania	5,9	31417513
Poola	5,2	24014336
Ungari	3,6	6254101
Kreeka	3,0	6657643
Bulgaaria	2,5	4047300
Rumeenia	1,3	12247111
Türgi	1,2	57459186

Allikas: Eurostat

Kui arvutaksime osakaaludest lihtsalt aritmeetilise keskmise, liidetaks osakaalud kokku ja jagataks riikide arvuga. R-s oleks vastav kaalumata keskmise arvutamise tehe järgmine:

library(tidyverse) # laeme andmetöötlust hõlbustava paketi tidyverse

lang_pop |>    # `lang_pop` on objekt, milles asuvad eelneva tabeli andmed
  summarise(kaalumata_keskmine = sum(osakaal) / n()) # käsk n() annab ridade arvu andmestikus (riikide arvu)

# A tibble: 1 × 1
  kaalumata_keskmine
               <dbl>
1               18.6

Elanike arvuga kaalutud aritmeetilise keskmise puhul korrutatakse iga riigi puhul osakaal elanike arvuga, need korrutised liidetakse ja jagatakse läbi mitte riikide arvuga, vaid kõigi riikide elanike koguarvuga:

lang_pop |>
  summarise(kaalutud_keskmine = sum(osakaal * elanike_arv) / sum(elanike_arv))

# A tibble: 1 × 1
  kaalutud_keskmine
              <dbl>
1              11.4

Loomulikult on R-s ka kaalumata ja kaalutud keskmiste arvutamiseks omaette funktsioonid mean ja weighted.mean, mis annavad sama tulemuse.

lang_pop |>
  summarise(kaalumata_keskmine = mean(osakaal))

# A tibble: 1 × 1
  kaalumata_keskmine
               <dbl>
1               18.6
lang_pop |>
  summarise(kaalutud_keskmine = weighted.mean(osakaal,
          w = elanike_arv)) # argumendile w tuleb omistada kaalutunnuse nimi andmestikus
# A tibble: 1 × 1
  kaalutud_keskmine
              <dbl>
1              11.4

Eelnevas näites olid meil riigi tasandile agregeeritud andmed ehk inimeste keeleoskuse andmete põhjal olid arvutatud iga riigi kohta kokkuvõtlikud näitajad. Analüüsides küsitlusandmeid, on enamasti tarvis kaaluda mitte agregeeritud, vaid indiviiditasandi andmeid ehk andmestikku, kus on iga vastaja kohta eraldi andmerida. Järgnevalt vaatlemegi lähemalt andmete kaalumist küsitlusandmete kontekstis ehk juhul, kui analüüsime valikuuringu indiviiditasandil andmeid ja soovime tulemusi üldistada populatsioonile.

Laias laastus on küsitlusandmete kaalumise eesmärk arvutada võimalikult täpsed hinnangud (üldisemalt öeldes statistilised näitajad, olgu need aritmeetilised keskmised või protsentnäitajad või muud keerulisemad näitajad) populatsiooni kohta. Iga indiviidi kaalutakse n-ö üles või alla, nii et ta esindaks kas suuremat või väiksemat hulka populatsiooni liikmetest, vastavalt sellele, kas grupp, mida see indiviid esindab, on küsitlusandmetes ala- või üleesindatud. Teisiti sõnastades on kaalumise eesmärk tõsta küsitlusandmete esinduslikkust populatsiooni suhtes.

Eelnevast nähtub, et kuna esinduslikkust on tarvis tõsta, siis peitub siin varjatud eeldus, et küsitlusandmed ei esinda populatsiooni piisavalt täpselt, st vastajate kogum ei ole täpne vähendatud koopia populatsioonist. Täpsemalt öeldes, kui uurida erinevate vastajaid kirjeldavate tunnuste jaotust vastajate seas ja populatsioonis (olgu need siis vanus, sugu, haridustase vms), siis esineb küsitlusandmete puhul ka parimat praktikat järgides võetud valimi korral nendes jaotustes suuremaid või väiksemaid erinevusi. See on paratamatu, sel on erinevaid põhjuseid ja seetõttu on ka erinevaid võtteid ja meetodeid andmete kaalumiseks. Käesolevas peatükis vaatlemegi neist mõningaid, et selgitada, miks ja mis juhtudel on tarvis andmeid kaaluda ja kuidas seda teha.

Vabalt kasutada olevates küsitlusandmestikes on tavaliselt kaalutunnused, mille abil andmeid kaaluda, juba olemas, st kaale ei tule ise arvutada. Sellegipoolest eeldab ka olemasolevate kaalude kasutamine kursis olemist sellega, kuidas need andmed on kogutud, sh kuidas on koostatud küsitluse aluseks olnud valim. Järgnevalt käsitlemegi eri liiki kaale, nende eesmärke ja seda, kuidas kaalude valik on seotud valimiga. Selles orienteerumiseks on vaja tunda eri valimitüüpe ja nende eripärasid – heaks võimaluseks ennast nendega kurssi viia on läbi töötada SAMMu valimite peatükk.

Disainikaalude põhimõte ja eesmärk

Lihtsa juhuvalimi puhul on kõigil populatsiooni liikmetel võrdne tõenäosus valimisse sattuda. Kiht-, klaster- või mitmeastmelise valimi puhul võivad need tõenäosused – neid nimetatakse kaasamistõenäosusteks – aga erineda. Kihtvalimi puhul jaotatakse populatsioon valitud tunnus(t)e alusel kihtideks ja tehakse juhuvalik iga kihi sees eraldi, see tõstab valimi esinduslikkust populatsiooni suhtes. Proportsionaalse kihtvalimi puhul on kihtide proportsioonid valimis samad, mis populatsioonis. Vahel võidakse aga otsustada mitteproportsionaalse kihtvalimi kasuks, kus mõne grupi proportsioon valimis võib olla suurem või väiksem kui populatsioonis. Näiteks Eesti Integratsiooni Monitooringu puhul kasutatakse valimit, kus eestlasi ja mitte-eestlasi on sama palju, olgugi et Eesti rahvastikus ehk populatsioonis on mitte-eestlasi oluliselt vähem. Selle eesmärk on küsitlusandmete põhjal neid kaht gruppi võrreldes teha mitte-eestlaste kohta samavõrd täpseid järeldusi kui eestlaste kohta. Kui aga soovitakse neid kaht gruppi analüüsida mitte võrdlevalt, vaid koos (nt mitte arvutada mingi tunnuse aritmeetilised keskmised eestlaste ja mitte-eestlaste kohta eraldi, vaid hinnata selle tunnuse keskmist Eesti rahvastikus tervikuna), on tarvis andmeid kaaluda, et saada mitteproportsionaalse kihtvalimi andmed proportsionaalseks populatsiooniga. Sellisel juhul kasutatakse kaale, mida nimetatakse disainikaaludeks. Disainikaalude eesmärk ongi tõsta küsitlusandmete esinduslikkust populatsiooni suhtes, võttes arvesse valimiliikmete erinevaid kaasamistõenäosusi. Disainikaalud arvutatakse nii, et iga indiviidi disainikaalu väärtus on pöördvõrdeline selle indiviidi kaasamistõenäosusega valimisse. Selgitame seda konkreetse näite varal lähemalt järgmises osas.

Samamoodi on enamasti tarvis andmeid disainikaalude abil kaaluda, kui andmed on kogutud klaster- või mitmeastmelise valimi abil. Mitmeastmelise valimitüübi puhul tehakse valik mitmel tasandil, näiteks õpilaste küsitlemise puhul lihtsustab küsitlustööd valim, kus esmalt valitakse koolid (esmane valikutasand on kool), seejärel koolidest klassid (teisene valikutasand) ja klassidest kas kõik õpilased või osa neist (kolmas valikutasand). Selliselt valimi koostamine küll lihtsustab andmekogumist ja nõuab vähem ressursse, kuid eri koolide ja klasside õpilasi tervikuna uurides tuleb arvestada, et õpilaste kaasamistõenäosused erinevad – teisiti öeldes, eri õpilaste tõenäosus valimisse sattuda on erinev, sõltuvalt sellest, kui palju on koolis klasse ja kui palju on klassis õpilasi. Et teha kogu õpilaskonna ehk populatsiooni suhtes esinduslikke järeldusi, tuleb andmeid kaaluda disainikaaludega, nii et õpilased, kellel oli väiksem võimalus valimisse sattuda, omandaksid analüüsis suurema kaalu (n-ö esindaksid rohkem õpilasi), ja õpilased, kellel oli suurem võimalus valimisse sattuda, omandaksid väiksema kaalu.

Disainikaalude arvutamine

Selgitame disainikaalude arvutamist mitmeastmelise valimi puhul Dillmani jt (2014:87-88) näite varal. Uuringus, mille populatsiooniks on teatud regiooni elanikud, koostatakse kaheastmeline valim: esmasel valikutasandil valitakse 10 000 leibkonna seast juhuslikkuse alusel 1000 leibkonda, teisel valikutasandil valitakse igast leibkonnast juhuslikkuse alusel üks leibkonnaliige. Esimesel valikutasandil on iga leibkonna kaasamistõenäosus ehk tõenäosus sattuda valimisse 1/10 ehk 0,1. Iga inimese kaasamistõenäosus seevastu sõltub sellest, kui palju on tema leibkonnas liikmeid: kaheliikmelises leibkonnas on iga liikme tõenäosus sattuda valimisse 1/10 (leibkonna kaasamistõenäosus) * 1/2 (leibkonnaliikme kaasamistõenäosus) = 1/20 ehk 0,05. Sellise indiviidi disainikaalu väärtus on pöördvõrdeline tema kaasamistõenäosusega ehk 1 / 0,05 = 20. Viieliikmelises leibkonnas on iga liikme kaasamistõenäosus 1/10 * 1/5 = 1/50 ehk 0,02; sellise indiviidi disainikaal on 1 / 0,02 = 50.

Tabel 2. Disainikaalude arvutamine kaasamistõenäosuste põhjal mitmeastmelise valimi näitel

Indiviid, kelle leibkonnas on…	Leibkonna kaasamistõenäosus	Indiviidi kaasamistõenäosus leibkonnast	Indiviidi kaasamistõenäosus populatsioonist	Indiviidi disainikaal
üks liige	1/10	1/1	1/10	10
kaks liiget	1/10	1/2	1/20	20
kolm liiget	1/10	1/3	1/30	30
neli liiget	1/10	1/4	1/40	40
viis liiget	1/10	1/5	1/50	50

Allikas: Dillman jt (2014: 88)

Tabelis 2 arvutatud disainikaalud näitavad, kui mitut populatsiooni liiget mingi valimiliige esindab. See tähendab, et kui arvutaksime selles näites kõigile 1000 valimiliikmele disainikaalud, siis nende summa oleks sama, mis inimeste arv selles regioonis ehk populatsioonis. Praktikas võime andmestikes seevastu kohata disainikaale, kus suur osa kaalude väärtustest jääb 1 ligidale. Sellisel juhul on eelneva näite kohaselt saadud disainikaalud (ehk kaasamistõenäosuste pöördväärtused) jagatud läbi kaalude aritmeetilise keskmisega. Selle tulemusena on disainikaalude aritmeetiline keskmine 1 ning kaalude summa võrdub indiviidide arvuga valimis. Kasutades selliselt arvutatud kaale analüüsis, on kaalutud indiviidide arv võrdne mitte indiviidide arvuga populatsioonis, vaid indiviidide arvuga valimis. Sellist lähenemist kasutatakse küsitlusandmete kaalude arvutamisel üsna tihti ja sellisel kujul on kaalud ka näiteks Euroopa Sotsiaaluuringu andmestikes.

Millal on tarvis disainikaale kasutada?

Disainikaale on reeglina tarvis kasutada, kui andmed on kogutud tõenäosusliku valimi alusel, kasutades keerukamat valikutüüpi kui lihtne juhuvalim (st valik tehakse kihitatult või klastrite alusel). “Reeglina” ei tähenda siin seda, et kaalumise vallas ennast mitte eriti kindlalt tundes saab otsustada jätta andmed kaalumata, lootes, et ehk on mul tegu ühega neist ülejäänud, ebareeglipärastest juhtumitest. Otsus andmeid kaaluda või kaalumata jätta peaks põhinema konkreetsetel kaalutlustel, võttes lisaks valimi koostamise eripäradele arvesse, milline on analüüsiühik ehk mis on konkreetses olukorras kogum, millele soovime analüüsitulemusi üldistada.

Disainikaalude arvutamise näites, kus valik tehti esmalt leibkondade vahel ja seejärel leibkonnasiseselt, on andmeid kindlasti tarvis disainikaaludega kaaluda, kui soovime teha üldistusi selle regiooni elanike kohta (st kogum, millele soovime tulemusi üldistada, on regiooni elanikkond, mitte regiooni leibkonnad). Kui jätaksime sel juhul andmed disainikaaludega kaalumata, mõjutaksid väiksematest leibkondadest pärit vastajad tulemusi ebaproportsionaalselt rohkem. Kui aga soovime teha järeldusi regiooni leibkondade kohta – näiteks küsiti küsitluses andmeid ka leibkondade kohta, nagu leibkonna sissetulek –, siis pole andmeid disainikaaludega kaaluda vaja, sest valimi koostamisel oli esimesel valikutasandil kõigil leibkondadel samasugune tõenäosus valimisse sattuda (sest esimesel valikutasandil oli tegu ainult lihtsa juhuvalikuga). Esimeses, Integratsiooni Monitooringu näites on vaja andmeid kaaluda, kui analüüsime eestlaste ja mitte-eestlaste ehk erinevate mitteproportsionaalsete kihtide andmeid koos. Küll aga pole otsest vajadust andmeid kaaluda, kui analüüsime eestlasi ja mitte-eestlasi võrdlevalt, st erinevate kihtide andmeid eraldi.

Kao kompenseerimine

Disainikaalud võimaldavad elimineerida valimivõtu eripäradest tulenevat esinduslikkuse kadu. Samas esineb valikküsitluste puhul teisigi tegureid, mis võivad esinduslikkust populatsiooni suhtes vähendada, mille tõttu disainikaaludest ei pruugi kaalumisel piisata. Üks neist teguritest on mittevastamine ehk valimiliikmete kadu – kaugeltki mitte kõik valimiliikmed ei soovi või ei saa küsitluses osaleda.

Kui vastamismäär on valimi eri gruppides samasugune, siis ei vähenda mittevastamine veel andmete esinduslikkust – vastajate hulk on sel juhul küll mittevastamise tõttu väiksem ja seepärast ei pruugi olla võimalik nõrgemaid populatsioonis esinevaid tunnustevahelisi seoseid tuvastada, kuid andmete esinduslikkust see veel ei mõjuta. Enamasti ei ole vastamismäär valimi eri gruppides siiski ühetaoline, vaid erineb teatud määral. Kui vastamismäär eri gruppides, st mingite tunnuste lõikes, erineb (nt on vastamismäär nooremates vanusegruppides madalam), saab kannatada esinduslikkus nende tunnuste suhtes ja lisaks selliste tunnuste suhtes, mis on omakorda nende tunnustega seotud. Sellest järeldub, et vanuse näites ei tekiks esinduslikkuse probleemi juhul, kui mõõdaksime küsitlusega mingeid väärtushinnanguid, mis ei sõltu vanusest. Üldiselt ei ole see aga realistlik – väärtushinnangud, olgu need poliitilised, ühiskondlikud, religioossed või muud, ikkagi varieeruvad vanuse lõikes teatud määral. Kui vastamismäär valimi eri gruppides varieerub, ei saa reeglina eeldada, et see tulemuste esinduslikkust ei mõjuta, mistõttu võib olla vaja kaalumisel lisaks arvesse võtta mittevastamisest tulenevat esinduslikkuse kadu.

Selle jaoks on erinevaid võimalusi. Üks võimalus mittevastamise ehk kao kompenseerimiseks on leida tunnused, mille lõikes vastamismäär erineb ja mis on seotud muude tunnustega andmestikus, ja nende gruppides leida vastamistõenäosused ehk arvutada igas grupis

• respondentide (ehk uuringus osalenud valimiliikmete) disainikaalude summa,
• valimiliikmete (ehk uuringus osalenud ja mitteosalenud liikmete) disainikaalude summa,
• ja leida nende summade suhe ehk jagatis.

Iga respondendi disainikaal tuleb seejärel läbi korrutada eelnevalt kirjeldatud jagatise pöördväärtusega. (Lihtsa juhuvalimi puhul, kus kõigi valimiliikmete valimisse kaasamise tõenäosused on samad, saab nimetatud jagatise asemel kasutada lihtsalt vastamismäära grupis.) Tabeli 3 näites tähendaks see, et kõigi 15–24-aastaste respondentide disainikaal tuleks läbi korrutada 1,622-ga.

Tabel 3. Disainikaalude kalibreerimine vastamistõenäosuste alusel

	15–24	25–34	35–44	45–64	65+	Kokku
Valimimaht	202	220	180	195	203	1000
Vastajate arv	124	187	162	187	203	863
Disainikaalude summa valimis	30322	33013	27046	29272	30451	150104
Disainikaalude summa vastajate seas	18693	28143	24371	28138	30451
Vastamistõenäosus	0,6165	0,8525	0,9011	0,9613	1,0000
Vastamistõenäosuse pöördväärtus	1,622	1,173	1,110	1,040	1,000

Allikas: Lohr (2019: 341)

Eelnevalt kirjeldatud meetodil saame kohandada disainikaale nii, et andmete kaalumine vähendaks ka mittevastamisest tulenevat esinduslikkuse kadu (inglise keeles kutsutakse seda meetodit weighting class adjustment). Selle eeldus on, et gruppides, mille kohta vastamistõenäosused leiti, vastamistõenäosus ei varieeru. See tähendab, et kui disainikaalude kohandamiseks kasutatakse ainult vanusegrupiti arvutatud vastamistõenäosusi, siis vanusegrupi sees ei tohiks erineda näiteks meeste ja naiste vastamistõenäosused või vastamistõenäosused haridustasemeti vms. See on tugev eeldus, mida püütakse rahuldada vastamistõenäosuste arvutamisega rohkem kui ühe tunnuse lõikes, st rohkemates gruppides. Siiski ei saa gruppe olla ülemäära palju, sest osasse gruppidesse jääks siis liiga vähe vastajaid, mille tõttu võivad osa indiviidide kaalud olla väga suured, mis omakorda muudaks kaalutud analüüsitulemused n-ö ebastabiilseks.

Silmas tuleb pidada ka seda, et grupikuuluvus peab olema teada kõigi valimiliikmete kohta, st ka nende kohta, kes olid valimis, aga ei osalenud uuringus. See piirab kohandamiseks kasutatavate tunnuste hulka oluliselt, praktikas on nende tunnuste hulk piiratud valikuraamis olevate andmetega.

Järelkihitamine

Eelnevalt kirjeldatud kao kompenseerimise meetod ongi lihtsasti rakendatav juhul, kui meil on ligipääs andmetele ka mittevastanute kohta (st kogu valimi andmetele), enamasti on see ligipääs vaid uuringu korraldajatel. Kui kasutada on ainult küsitlusandmed ehk andmed küsitletute kohta, on lihtsam kohandada disainikaale järelkihitamise meetodil. See ei eelda andmete olemasolu mittevastanute kohta, küll aga eeldab järelkihitamise aluseks olevate (enamasti sotsiaaldemograafiliste) tunnuste ühisjaotuste olemasolu vastanute ja populatsiooni kohta. Vastanute kohta on võimalik need ühisjaotused arvutada küsitlusandmete põhjal, populatsiooni kohta võivad (sõltuvalt populatsiooni ja tunnuste spetsiifilisusest) ühisjaotused leiduda muudes allikates, näiteks riiklikus statistikas. Järelkihitamise meetodil disainikaalude kohandamine toimub analoogselt eespool kirjeldatud kao kompenseerimisega, ainuke erinevus on see, et arvutustes kasutatakse valimiliikmete disainikaalude summa asemel indiviidide arvu vastavas grupis populatsioonis. See muidugi eeldab, et respondentide disainikaalude summa põhineb disainikaaludel, mis ei ole läbi jagatud disainikaalude keskmisega, nagu küsitlusandmestikes võib disainikaalude puhul olla tehtud.

Erinevalt eelnevalt kirjeldatud kao kompenseerimise meetodist võimaldab järelkihitamine kompenseerida nii mittevastamisest kui kaetuse veast tulenevat esinduslikkuse kadu. Kaetuse viga tuleneb sellest, et valikuraam ehk loend populatsiooni liikmetest, mida kasutatakse valimi võtmisel, ei kata täpselt populatsiooni (nt võib valikuraamis esineda isikuid, kes on nüüdseks surnud, või võivad mõne isiku andmed esineda topelt).

Enne kaalumise praktilise osa juurde minekut väärib tähelepanu veel mõni tõsiasi. Kuigi kaalumine üldjuhul võimaldab tõsta andmete esinduslikkust ja saada populatsiooni kohta täpsemad hinnangud, ei saa kaalumist pidada mingiks imerohuks, mis muudab andmed täiesti esinduslikuks populatsiooni suhtes ja kõrvaldab andmetest kõik vead. Eelkõige käib see just kaalumismeetodite kohta, mis püüavad lahendada mittevastamisest tulenevaid probleeme (nagu varem kirjeldatud kao kompenseerimine ja järelkihitamine). Miks on see hoiatus oluline?

• Nagu juba öeldud, on neil kaalumismeetoditel üsna tugevad eeldused, mida täielikult rahuldada on keeruline, kui mitte võimatu.
• Pealegi on nende meetodite rakendamises alati teatud määral subjektiivsust, näiteks kaalumise aluseks olevate tunnuste valikul.
• Mil määral disainikaalude kohandamise meetodid mittevastamisest ja muudest uuringuvigadest tulenevaid probleeme konkreetsel juhul lahendavad ja andmete esinduslikkust parandavad, sõltub paljuski sellest, kas tegu on juhuslike või süstemaatiliste vigadega (juhuslikku ja süstemaatilist viga aitab mõtestada uuringu koguvea kontseptsioon, mille kohta on ülevaatlikuks sissejuhatuseks nt Fuchs (2008)). Mittevastamise puhul tähendab see laias laastus seda, kas uuringus osalenud valimiliikmete kogum (respondendid) ja mitteosalenud valimiliikmete kogum (mittevastanud) on mõõdetavate tunnuste poolest samasugused või mitte.
  • Kui on samasugused, töötavad disainikaalude kohandamise meetodid hästi (õieti pole neid otseselt vaja rakendadagi, sest sel juhul on vastanute kogum juba esinduslik ka populatsiooni suhtes). See on paraku ideaaljuhtum, mida esineb harva.
  • Kui ei ole samasugused, sõltub kaalumise edukus sellest, kuivõrd on need erinevused seletatavad kaalumise aluseks olevate tunnustega. Näiteks võib juhtuda, et vastanud ja mittevastanud erinevad mingite mõõdetud väärtushinnangute poolest. Kui kohandame sellisel juhul disainikaale, kompenseerides mittevastamist näiteks vanuse, soo ja elukoha alusel, aga mõõdetud väärtushinnangud on nimetatud tunnustega seotud ainult nõrgalt, ei paranda see väärtushinnangute analüüsil saadavate tulemuste esinduslikkust kuigivõrd. Ka juhul, kui kaalumise aluseks olevad tunnused on mõõdetavate tunnustega seotud, ei ole need seosed üksühesed; kõik mõõdetavad tunnused ei ole kaalumise aluseks olevate tunnustega ühtmoodi ja samavõrd tugevalt seotud, osa mõõdetavaid tunnuseid ei pruugi nendega üldse seotud olla.
• Kui tegu on süstemaatiliste vigadega, võib andmete kaalumine teatud juhtudel tulemuste esinduslikkust isegi halvendada. Näiteks on tänapäeval telefoniküsitlustes raskem vastama saada nooremaealisi. Võib eeldada, et need noored, kes võõrale numbrile vastavad, on üldiselt usaldavamad kui nende eakaaslased üldiselt. Seega, kui uuringuküsimustega mõõdetakse näiteks usaldustaset ühiskonnas, on küsitletute seas alaesindatud madalama usaldustasemega vastajad ning kaalumata tulemused näitavad usaldustaset kõrgemana, kui see tegelikult on. Kui sel juhul andmeid veel vanuse alusel kaaluda, st üles kaaluda nooremaid vastajaid, kes on niigi kõrgema usaldustasemega, näitaksid analüüsitulemused usaldustaset ekslikult veelgi kõrgemana. Seega on disainikaalude kohandamise jaoks tunnuste valikul (ja kohandatud kaalude kasutamisel) oluline arvesse võtta mitte ainult seda, millised tunnused on seotud mittevastamise ja teiste mõõdetavate tunnustega, vaid ka seda, millised need seosed on.
• Kaalud arvutatakse kompenseerima n-ö objekti kadu ehk nende valimiliikmete kadu, kes uuringus üldse ei osalenud. Samas esineb küsitlusandmetes ka küsimusele mittevastamist, kus muidu koostööaldis respondent ei soovi või ei oska mingile konkreetsele ankeediküsimusele vastust anda. Olenevalt küsimusest võib selline andmete kadu olla märkimisväärne – sellist kadu kaalumine ei kompenseeri (kui soovime, et kompenseeriks, tuleks arvutada uued, konkreetse küsimuse mittevastamist arvestavad kaalud).

Seega tuleks igasugustesse väidetesse, mis käsitlevad kaalutud andmeid kui esinduslike ja kallutamata tulemuste garantiid, suhtuda eluterve skepsisega. Üldjuhul kehtib reegel, et kehva või olematu metoodikaga kogutud andmete puhul ei aita ka kaalumine esinduslikkust parandada. Usaldusväärse uuringuraporti puhul peaks kaalumise läbipaistvuse tagamiseks olema välja toodud, kas ja kuidas andmeid kaaluti, kuidas olid kaalud koostatud, sh milliseid tunnuseid kaalude arvutamisel kasutati ja millistest allikatest saadi andmed populatsiooni kohta (nt järelkihitamise jaoks) (AAPOR, 2025).

Vaatame Euroopa Sotsiaaluuringu (ESS) näitel, kuidas kaaluda andmeid R-is (R Core Team, 2025). ESS-i andmestikes on disainikaalud tunnuses dweight, n-ö järelkihituskaalud ehk järelkihitamise alusel kohandatud disainikaalud on tunnuses pspwght. ESS-i andmeid analüüsides soovitatakse kasutada kaale, mis on järelkihitamisega kohandatud, sest need võimaldavad korrigeerida mittevastamisest jm vigadest tulenevaid nihkeid (European Social Survey, 2023). Järgnevates näidetes ongi kasutatud kaalumiseks tunnust pspwght.

Avame R-is ESS-i 10. küsitluslaine ehk 2020/21. aasta andmestiku, mis on alla laetud ESS-i andmeportaalist. Võtame näite aluseks andmed ühe riigi kohta, kus kasutati mitmetasemelist valikuskeemi (mitmetasemelise valimi puhul on kaalumise mõju tulemustele reeglina suurem). Meie näites on selliseks riigiks Kreeka, kus kasutati kolmeastmelist valimit (esimesel astmel valikuühikuks rahvaloenduse piirkond, teisel astmel sisuliselt leibkond, kolmandal leibkonnaliige) ning esimesel astmel kasutati ka kihitamist. See taustainfo on leitav ESS-i andmeportaali 10. küsitluslaine leheküljelt (Country documentation => Greece).

Loome uue andmeobjekti ess10 ja omistame sellele ESS-i 10. laine andmestiku, mille laeme R-i paketi haven funktsiooni read_sav abil.

ess10 <- haven::read_sav("data/ess10.sav")

gr10 <- ess10 |>
  filter(cntry == "GR") # filtreerime tunnuse cntry alusel Kreeka andmed


Andmete kaalumine kirjeldavas analüüsis

Kuidas arvutada R-is kirjeldavaid kaalutud näitajaid, st punkthinnanguid, nagu kaalutud aritmeetiline keskmine, kaalutud standardhälve või tunnuse kaalutud jaotus? Selleks saab kasutada R-i sisseehitatud pakettide (n-ö base R), paketi dplyr või muude pakettide võimalusi. Järgnevalt ongi toodud mõned punkthinnangute arvutamise näited.

Tunnuse kaalutud sagedusjaotuse arvutamine

Arvutame tunnuse netusoft (vastaja internetikasutuse sagedus) jaotuse funktsiooniga dplyr::count. Kui soovime kaalutud jaotust, tuleb käsku lisada argument wt, mille väärtuseks on kaalutunnus. Siinses näites arvutataksegi tunnuse netusoft kaalutud jaotus, mis esitatakse väljundtabelis veerus n; selle veeru väärtuste alusel arvutatakse funktsiooni mutate abil ka suhteline kaalutud jaotus ehk kaalutud protsentnäitajad. Pakett dplyr on osa tidyverse’ist (Wickham jt, 2019), mille laadisime alguses library-käsuga mällu, seetõttu pole tarvis dplyr’it eraldi laadida.

gr10 |>
  count(netusoft, wt = pspwght) |>
  mutate(protsent = n / sum(n) * 100)
# A tibble: 6 × 3
  netusoft                      n protsent
  <dbl+lbl>                 <dbl>    <dbl>
1  1 [Never]               514.     18.4
2  2 [Only occasionally]   117.      4.18
3  3 [A few times a week]  177.      6.31
4  4 [Most days]           309.     11.0
5  5 [Every day]          1676.     59.9
6  NA                        5.55    0.198

Kaalutud aritmeetilise keskmise arvutamine

Funktsioonil mean, millega saab R-is arvutada aritmeetilise keskmise, seevastu pole kaalumiseks eraldi argumenti (käivita funktsiooni nimi koos küsimärgiga nime ees, et näha, milliseid argumente funktsioon võimaldab kasutada). R-i põhipaketis on kaalutud keskmise arvutamiseks eraldi funktsioon weighted.mean, millel on andmete kaalumiseks argument w. Järgnevas näites arvutatakse tervishoiusüsteemiga rahulolu (tunnus stfhlth) kaalutud keskmine, võttes abiks funktsiooni dplyr::summarise.

gr10 |>
  summarise(stfhlth_kesk = weighted.mean(stfhlth, w = pspwght, na.rm = TRUE))     # funktsioon weighted.mean nõuab argumenti na.rm = TRUE, et arvutusest jäetaks välja indiviidid, kellel esineb tunnuses stfhlth andmelünk
# A tibble: 1 × 1
  stfhlth_kesk
         <dbl>
1         4.43

Muude kaalutud jaotusparameetrite arvutamine

Mitmeid erinevaid jaotusparameetreid saab arvutada näiteks paketis TAM olevate funktsioonide abil (vt lähemalt käsuga ?TAM::weighted_mean)

library(TAM)

gr10 |>
  summarise(stfhlth_kesk = weighted_mean(stfhlth, w = pspwght),
            stfhlth_sthälve = weighted_sd(stfhlth, w = pspwght),
            stfhlth_asümmeetria = weighted_skewness(stfhlth, w = pspwght),
            stfhlth_järskus = weighted_kurtosis(stfhlth, w = pspwght))
# A tibble: 1 × 4
  stfhlth_kesk stfhlth_sthälve stfhlth_asümmeetria stfhlth_järskus
         <dbl>           <dbl>               <dbl>           <dbl>
1         4.43            2.31            -0.00704          -0.989

Andmete kaalumine järeldavas analüüsis

Eelnevad andmete kaalumise näited olid punkthinnangute kohta. Tulenevalt asjaolust, et analüüsime valimi andmeid, mitte kogu populatsiooni, ei pruugi punkthinnang siiski populatsiooni täpselt kirjeldada (ka kaalumisest hoolimata). Ka parimate valimi koostamise ja kaalumise praktikate puhul esineb enamasti teatud viga selle tõttu, et juhuslikkuse alusel võetud valim võib populatsioonist mõnevõrra erineda – indiviidide jaotus (nt sotsiaaldemografiliste või mis tahes muude tunnuste alusel) võib valimis teatud määral erineda jaotusest populatsioonis. Et saada populatsiooni kohta täpsemad hinnangud, peaksime kasutama lisaks kirjeldavatele näitajatele ka järeldavat analüüsi, näiteks arvutama lisaks punkthinnangutele ka vahemikhinnangud (usalduspiirid) ja seoste või erinevuste esinemise hindamiseks populatsioonis läbi viima statistilisi teste.

Kuidas kaaluda R-is andmeid järeldavas analüüsis? R-is on erinevates pakettides funktsioone statistiliste testide jaoks, mis võimaldavad andmeid kaalutunnuse alusel kaaluda, nt weights::wtd.t.test kaalutud t-testi jaoks. Selline, ainult kaalutunnuse arvestamine andmete kaalumisel, on järeldavas analüüsis adekvaatne lähenemine juhul, kui andmed on saadud lihtsa juhuvaliku alusel. Kui aga on kasutatud keerukamat tõenäosuslikku valimit (ja tihtilugu on küsitlusuuringutes seda tehtud), ei pruugi lihtsalt kaalutunnusega kaalumisest järeldaval analüüsil täpsete tulemuste saamiseks piisata – siin on kaalumisel tarvis täpsemalt arvesse võtta ka valimivõtu eripärasid ehk valikudisaini, mida on valimi koostamisel kasutatud. Lihtsustatult öeldes tähendab see mitte ainult kaasamistõenäosuste erinevuste arvesse võtmist, vaid ka selle arvestamist, millised indiviidid asuvad millistes kihtides ja/või klastrites.

Miks piisab järeldavas analüüsis lihtsa juhuvalimi korral pelgalt kaalumisest, aga keerulisema valikuskeemi puhul tuleb arvestada valikudisainiga? Kihtvalimi puhul jaotatakse populatsioon kihtideks ja juhuslik valik tehakse kihtide sees. See vähendab valimi hajuvust ning reeglina parandab valimi esinduslikkust populatsiooni suhtes, mille tõttu on näiteks punkthinnangute standardvead mõnevõrra väiksemad, kui tavalised, lihtsa juhuvalimi jaoks mõeldud standardvea arvutamise meetodid võimaldaksid järeldada. Klastrite puhul ei ole valimiliikmed üksteisest sõltumatud – kuna klastrid moodustatakse mingi tunnuse alusel, on see siis elukoht või õppimine mingis koolis ja klassis, on ühes klastris olevad liikmed üksteisega enamasti mõnevõrra sarnasemad kui muude klastrite liikmetega. See suurendab mõõdetavate tunnuste hajuvust ja omakorda punkthinnangute standardvigu. Andmete kaalumisel seda klastritesisest homogeensust ja klastritevahelist heterogeensust ehk valikudisaini arvestamata jättes hindaksime järeldaval analüüsil andmete täpsust üle ehk saaksime näiteks punkthinnangutele kitsamad usaldusvahemikud, kui oleks tegelikult kohane.

R-is võimaldavad andmete kaalumisel valikudisaini arvestada näiteks paketid survey (Lumley, 2010) ja selle põhjal koostatud pakett srvyr (Freedman Ellis ja Schneider, 2024). Pakett survey on vanem ja täielikum, samas on srvyr lihtsam kasutada neile, kes on R-is harjunud tidyverse’i süntaksiga, ja võimaldab käskudesse integreerida dplyr’i funktsioone.

Mõlema paketi võimaluste kasutamiseks tuleb esmalt seadistada andmete kaalumine ja valikudisain, paketis srvyr on selleks funktsioon as_survey_design. Selle funktsiooni põhilised argumendid on

• .data ehk andmestik;
• ids; selle väärtuseks tuleb omistada andmestikust tunnus(ed), mis sisaldab/-vad infot selle kohta, millisesse klastrisse vastaval andmereal olev indiviid kuulub. ESS-i andmestikes on taoline info tunnuses psu;
• strata, mille väärtuseks saab antud näites stratum ehk andmestikust tunnus, milles on kirjas, millisesse valikukihti mingi indiviid kuulus (juhul, kui valimi võtmisel kasutati kihte ehk populatsioon jaotati kihtideks).
• weights ehk kaalutunnus.

Paketid survey ja srvyr eeldavad vaikimisi, et andmeid kaalutakse disainikaaludega. Et järelkihitamist või muud disainikaalude kohandamist järeldaval analüüsil täpselt arvesse võtta, tuleks kohandatud kaalud uuesti kalibreerida. See on võimalik (vt täpsemalt siit), aga ESS-i andmete puhul keerulisem, sest ESS-i andmestikes on kaalud kujul, kus kaalude summa on ligikaudu võrdne indiviidide arvuga andmestikus, mitte indiviidide arvuga populatsioonis. Alternatiiv, mida praktikas tihtipeale kasutatakse, on käsitleda kohandatud kaale, justkui oleks tegu tavaliste disainikaaludega, mis uuesti kalibreerimist ei nõua. Sellega saadakse küll mõnevõrra konservatiivsemad hinnangud (nt mõnevõrra laiemad usaldusvahemikud kui järelkihitatud disainikaalud tegelikult eeldaks), aga erinevus ei ole enamasti suur (Lumley, 2021). Ka ESS-i andmete kaalumise juhend pakub välja sellise lähenemise, seda on ka järgnevas käsus kasutatud, kus argumendi weights väärtuseks on pspwght.

library(srvyr)

gr10w <- as_survey_design(.data = gr10, ids = psu, strata = stratum, weights = pspwght)

Usalduspiiride arvutamine kaalutud andmetega

Valikudisaini objekti ee10w ehk objekti, kus on koos küsitlusandmestik koos valikudisaini ja kaalumise seadistusega, saab kasutada sisendina järeldavas analüüsis, näiteks standardvigade/usalduspiiride arvutamiseks või statistiliste testide jaoks. Selle jaoks tuleb kasutada vastavaid srvyr või survey pakettide funktsioone, näiteks aritmeetilise keskmise ja selle standardvea/usalduspiiride arvutamiseks ei saa kasutada lihtsalt funktsiooni weighted.mean vms, vaid tuleb kasutada funktsioone srvyr::survey_mean või survey::svymean. Siinkohal on toodud kaalutud keskmiste arvutamise näide neist esimesega; argumendiga vartype saab selle funktsiooni puhul seadistada usalduspiiride või muude näitajate arvutamise ("ci"), vaikeseadena arvutatakse muidu ainult keskmise standardviga ("se"). Allolevas näites arvutatakse keskmine rahulolu tervishoiusüsteemiga ja selle standardviga ja usalduspiirid tervisehinnangu lõikes (eelnevalt kodeeritakse väga halva tervisehinnanguga vastajad, keda on väga vähe, kokku halva tervisehinnanguga vastajatega), lisaks arvutatakse summarise-käsus kaalutud vastajate arv (esitatakse väljundtabeli veerus n). Usalduspiirid arvutatakse vaikimisi usaldusnivool 95%, vajadusel saab seda muuta survey_mean argumendi level abil (kõigi argumentide vaikeseadeid ja võimalike sätteid saab uurida käsuga ?survey_mean).

gr10w |>
  mutate(health4 = case_match(health,
                              5 ~ 4,
                              .default = health)) |>
  group_by(health4) |>
  summarise(stfhlth_kesk = survey_mean(stfhlth, na.rm = TRUE, vartype = c("se", "ci")),
            n = sum(pspwght))
# A tibble: 5 × 6
  health4        stfhlth_kesk stfhlth_kesk_se stfhlth_kesk_low stfhlth_kesk_upp      n
  <dbl+lbl>             <dbl>           <dbl>            <dbl>            <dbl>  <dbl>
1  1 [Very good]         4.35           0.142             4.07             4.63  1250.
2  2 [Good]              4.64           0.168             4.30             4.97   999.
3  3 [Fair]              4.47           0.198             4.08             4.86   431.
4  4 [Bad]               3.48           0.334             2.82             4.14   115.
5  NA                    1              0                 1                1        4.00

Funktsiooniga srvyr::survey_prop saab arvutada tunnuse kaalutud jaotuse, grupeerides eelnevalt andmestiku selle tunnuse alusel, mille jaotust soovime saada. Arvutame siinkohal internetikasutuse sageduse kaalutud jaotuse ning osakaalude standardvead ja usalduspiirid.

gr10w |>
  group_by(netusoft) |>
  summarise(prop = survey_prop(vartype = c("se", "ci")))
# A tibble: 6 × 5
  netusoft                   prop prop_se prop_low prop_upp
  <dbl+lbl>                 <dbl>   <dbl>    <dbl>    <dbl>
1  1 [Never]              0.184   0.0128  0.160     0.210
2  2 [Only occasionally]  0.0418  0.00595 0.0315    0.0552
3  3 [A few times a week] 0.0631  0.0102  0.0458    0.0865
4  4 [Most days]          0.110   0.0118  0.0891    0.136
5  5 [Every day]          0.599   0.0229  0.553     0.643
6  NA                     0.00198 0.00102 0.000717  0.00548

Järgnev näide ilmestab andmete kaalumise ja valikudisaini arvesse võtmise mõju analüüsitulemustele. Arvutatakse tunnuse netusoft kaalutud jaotus ja osakaalude usalduspiirid usaldusnivool 95%, kasutades erinevaid kaalumise seadeid. Joonisel 2 esitatakse suurima osakaalu (internetti igapäevaselt kasutavate inimeste protsent) punkt- ja vahemikhinnang (usaldusnivool 95%) eri kaalumise seadete korral.

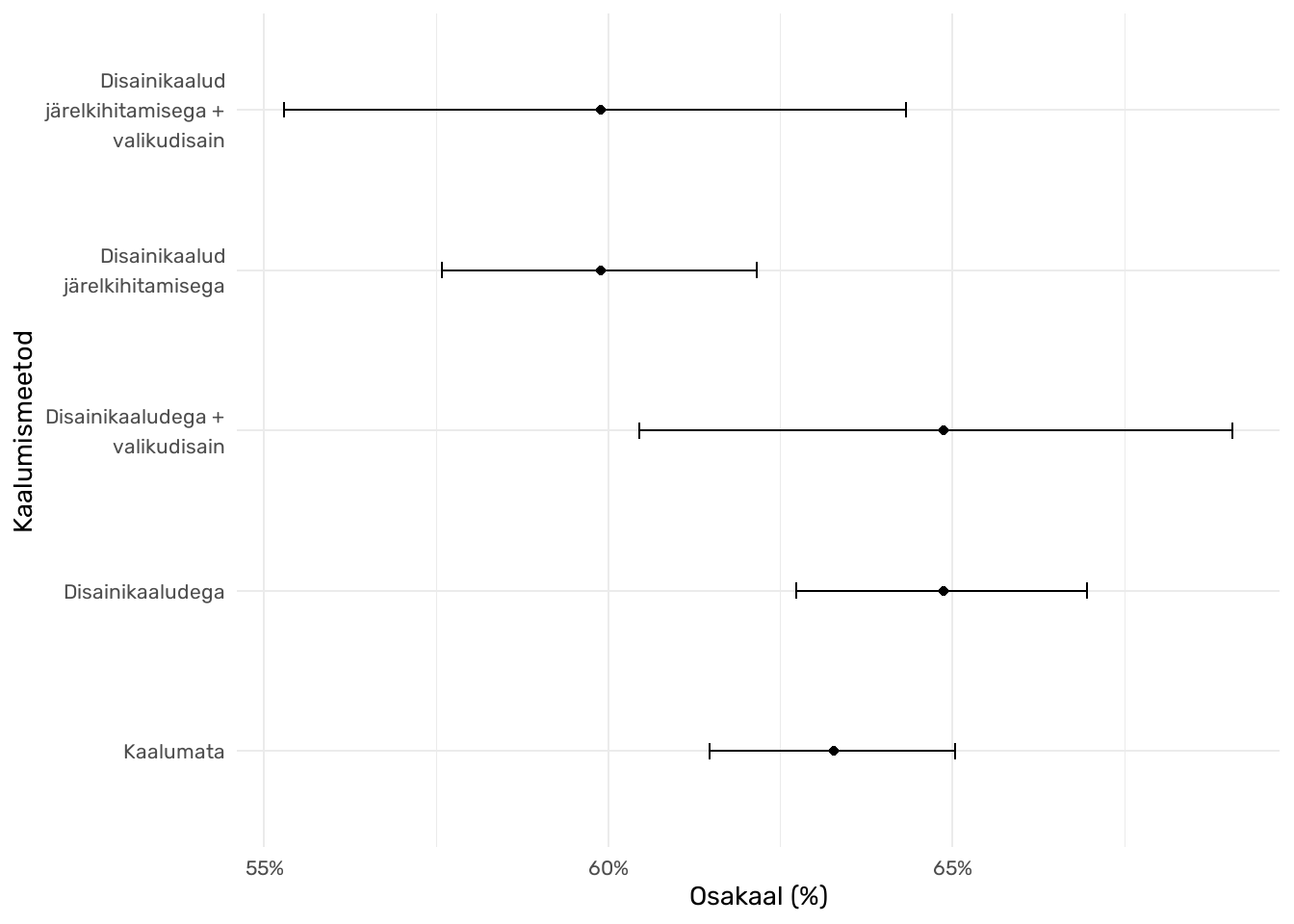
Joonis 2. Kreekas internetti igapäevaselt kasutavate inimeste osakaalu punkt- ja vahemikhinnang (usaldusnivool 95%) eri kaalumise seadete korral. Allikas: ESS 10. küsitluslaine

Jooniselt 2 ilmneb, et kui kasutada osakaalu arvutamisel ainult disainikaale, on punkthinnang antud juhul paari protsendipunkti võrra kõrgem ja selle usaldusvahemik natuke laiem, kui andmed kaalumata jättes. Üldjuhul ongi nii, et kaalumisel võib usaldusvahemik muutuda mõnevõrra laiemaks, sest kaalumine suurendab variatiivsust andmetes. Kui lisaks disainikaaludega kaalumisele võtta arvesse ka valikudisaini, jääb punkthinnang võrreldes ainult kaalumisega samaks, ent märkimisväärselt suureneb usaldusvahemik. See tuleneb asjaolust, et nüüd arvestatakse usalduspiiride arvutamisel ka valimi võtmisel kasutatud mitmeastmelise valikuga (ühes piirkonnas asuvad leibkonnad on keskmiselt üksteisega sarnasemad kui teiste piirkondade leibkondadega).

Samalaadseid erinevusi võrreldes kaalumata andmetelt tehtud arvutustega näeme ka juhul, kui disainikaale on kohandatud järelkihitamise alusel. Põhjus, miks punkthinnangud sel juhul eelnevaga võrreldes erinevad, tuleneb erinevast vastamismäärast eri interneti kasutamise sagedusega valimiliikmete seas (täpsemalt öeldes küll sellest, kuidas interneti kasutamise sagedus on seotud järelkihitamise aluseks olevate tunnustega ja vastamismäärast nende tunnuste lõikes).

Olulised järeldused jooniselt 2 on, et andmeid kaalumata võime eksida punkthinnangutes (ja sellest tulenevalt ka usalduspiiride väärtustes), valikudisaini arvestamata jättes võime alahinnata vahemikhinnangute laiust ehk määramatust valimi alusel leitavates hinnangutes. Kasutades disainikaale ilma järelkihitamiseta, saame küll arvutada näitajad, mis arvestavad valimivõtu eripäradega, ent ei arvesta mittevastamisest lähtuva esinduslikkuse vähenemisega. Seega, eeldusel, et järelkihitamisel on kasutatud sobivaid tunnuseid, mis on seotud mittevastamise mustrite ja analüüsitavate tunnustega, võimaldab järelkihitamisega kohandatud disainikaalude rakendamine koos valikudisaini arvesse võtmisega leida täpsemad hinnangud.

Statistiliste testide läbiviimine kaalutud andmetega

Paketid srvyr ja survey võimaldavad kaalutud andmetega läbi viia ka statistilisi teste. Need paketid töötavad koos: näiteks funktsioon svyttest, millega saab teha t-testi, on paketis survey, kuid selle sisendiks sobib meie varasemalt srvyr-i abil koostatud valikudisaini objekt gr10w.

Testime näitena, kas meeste ja naiste keskmine rahulolutase tervishoiusüsteemiga erineb. Funktsioon svyttest nõuab argumendi formula väärtusena testitavat mudelit valemi kujul, kus tildest ehk ~-märgist vasakul pool on t-testi puhul arvuline tunnus, mille keskmisi võrreldakse (antud juhul rahulolu tervishoiusüsteemiga) ja paremal pool kategoriaalne tunnus (siin sugu). Argumendi design väärtuseks peab olema valikudisaini objekt, mis meil on juba eelnevalt defineeritud gr10w.

library(survey)

svyttest(formula = stfhlth ~ gndr, design = gr10w)
    Design-based t-test

data: stfhlth ~ gndr
t = -0.035822, df = 175, p-value = 0.9715
alternative hypothesis: true difference in mean is not equal to 0
95 percent confidence interval:
-0.2228339 0.2148890
sample estimates:
difference in mean
      -0.003972449

Kaalutud t-testi tulemuste tõlgendus järgib sama loogikat, mida kasutatakse kaalumata andmete puhul. Antud juhul näitavad tulemused, et pole alust väita meeste ja naiste keskmise rahulolutaseme erinevust: t-statistiku olulisuse tõenäosus on kõrge (p = 0,972) ja ka keskmiste erinevuse usalduspiirid on nullile lähedal.

Paketi survey abil saab kaalutud andmete põhjal koostada ka üldistatud lineaarseid regressioonimudeleid, Coxi regressioonimudeleid ja loglineaarseid mudeleid ning kasutada muid analüüsimeetodeid. Vt lähemat infot paketi (Lumley, 2024) veebilehelt.

Populatsioonikaaludega kaalumine Euroopa Sotsiaaluuringu andmetes

Euroopa Sotsiaaluuringu andmete kaalumise kohta olgu veel öeldud, et andmestikus on lisaks kaalutunnus pweight. Tegu on populatsioonikaaludega, mis võtavad arvesse asjaolu, et elanike arv erineb riigiti kordades, samas kui vastajate arv on riigiti samas suurusjärgus. Populatsioonikaale oleks tarvis kasutada juhul, kui analüüsitakse mitme riigi andmeid koos, st kogum, millele tulemusi soovitakse üldistada, pole ühe riigi elanikkond, vaid mitme riigi elanikkond tervikuna. See tähendab, et soovime teha järeldusi riikideülese regiooni kui terviku kohta, näiteks soovime teada, milline on üldistatud usalduse tase Baltikumis tervikuna või milline on seos sisserändesse suhtumise ja vanuse vahel Põhjala regioonis üldiselt. Ilma populatsioonikaale kasutamata oleksid väiksemate riikide vastajad tulemustes üleesindatud.

Kui soovime populatsioonikaale kasutada, ei tohiks andmeid lihtsalt kaaluda tunnusega pweight, vaid arvestada tuleks ka disainikaale ja nende järelkihitamisega kohandamist. Seetõttu tuleks populatsioonikaalud läbi korrutada järelkihitamisega kohandatud disainikaaludega ja kaaluda andmestikku saadud korrutiste alusel:

gr10 <- gr10 |>
  mutate(anweight = pspwght * pweight)

Alates 9. küsitluslainest on see tehe juba andmete kasutaja eest ära tehtud, st nende lainete andmestikes on juba ka tunnus anweight. ESS-i kaalumise juhendites (European Social Survey, 2025) üldiselt soovitataksegi igasugustes analüüsides kasutada seda kaalutunnust. Käesolevas SAMM-u peatükis, kus tegeletakse ainult ühe riigi andmete analüüsiga, on siiski läbivalt kasutatud kaalumiseks tunnust pspwght. Selle eelis on, et ühe riigi andmeid (või riike võrdlevalt, eri kogumitena) analüüsides on indiviidide kaalutud koguarv sama, mis indiviidide koguarv kaalumata andmestikus. See võimaldab andmetes paremini orienteeruda – tunnusega anweight andmeid kaaludes oleks näiteks Eesti vastajate kaalutud koguarv saja-paarisaja ringis, mis on informatiivne ainult juhul, kui analüüsime eri riikide andmeid ühe tervikuna.

AAPOR. (2025). Disclosure Standards. https://aapor.org/standards-and-ethics/disclosure-standards/.

Dillman, D. A., Smyth, J. D., & Christian, L. M. (2014). Internet, phone, mail, and mixed-mode surveys: The tailored design method. John Wiley & Sons.

European Social Survey. (2023). ESS Weighting Data. https://www.europeansocialsurvey.org/sites/default/files/2023-06/ESS_weighting_data_1_1.pdf.

European Social Survey. (2025). ESS Methodology: Data Processing and Archiving – Weighting. https://www.europeansocialsurvey.org/methodology/ess-methodology/data-processing-and-archiving/weighting.

Freedman Ellis, G., & Schneider, B. (2024). srvyr: ’dplyr’-Like Syntax for Summary Statistics of Survey Data. http://gdfe.co/srvyr/

Fuchs, M. (2008). Total Survey Error (TSE). P. J. Lavrakas (Toim), Encyclopedia of Survey Research Methods (lk 897–902). Sage Publications. https://doi.org/10.4135/9781412963947.n585

Lohr, S. L. (2019). Sampling: design and analysis. Chapman; Hall/CRC.

Lumley, T. (2010). Complex Surveys: A Guide to Analysis Using R: A Guide to Analysis Using R. John Wiley; Sons.

Lumley, T. (2021). Using post-stratification weights in R survey package. Cross Validated. https://stats.stackexchange.com/q/540570

Lumley, T. (2024). survey: analysis of complex survey samples.

R Core Team (2024). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/.

Wickham et al., (2019). Welcome to the tidyverse. Journal of Open Source Software, 4(43), 1686, https://doi.org/10.21105/joss.01686