
Sotsiaalse Analüüsi Meetodite ja Metodoloogia õpibaas
Kirjeldav statistika
Kadri Rootalu
2014
Selles osas antakse ülevaade sellest, kuidas teha kvantitatiivsete andmete esmaanalüüsi. Kõige otstarbekam oleks analüüsimeetodi valikul lähtuda ankeedis kasutatud küsimuste või andmestikus olemasolevate tunnuste tüüpidest.
Peaaegu kõigi tunnuse tüüpide puhul on kõige lihtsamaks andmete kirjeldamise viisiks sagedusjaotuse või sagedustabeli koostamine (vt tabel 1) Sagedustabel on tabel, kus on esitatud
- tunnuse väärtuste loetelu ehk selle puhul esinenud vastusevariantide nimekiri (tabel 1 esimene veerg);
- väärtuste esinemise sagedus kas arvudena (tabel 1 teine veerg) või suhtelise sagedusena (tabel 1 kolmas veerg). Suhtelisi sagedusi võib esitada ka protsentides (tabel 1 neljas veerg);
- kumulatiivne ehk kogunev sagedus, mille puhul liidetakse kokku kõik vastaval real või eelmistel ridadel olnud vastusevariantide sagedused (tabel 1 viimane veerg).
Tabel 1. Vastajate haridustaseme jaotus
|
Vastajate arv |
Suhteline sagedus |
Suhteline sagedus (%) |
Kumulatiivne suhteline sagedus |
|
|
Keskharidus |
40 |
0,20 |
20% |
20% |
|
Kutseharidus |
70 |
0,35 |
35% |
55% |
|
Kõrgharidus |
90 |
0,45 |
45% |
100% |
|
Kokku |
200 |
1 |
100% |
Tõenäoliselt kõige sagedamini kasutatav näitaja statistilisel andmete analüüsis on aritmeetiline keskmine ehk keskväärtus. Selle saamiseks liidetakse kokku kõigi vastajate antud tunnuste väärtused ja jagatakse saadud summa vastajate arvuga. Tulemuseks on näitaja, mida võib käsitleda kui tüüpilist või läbilõikelist vastust vaatlusalusele küsimusele.
Kuna keskmine on leitud kõigi vastajate peale kokku, siis võib sellel olla ka väärtus, mida tegelikult ükski vastajatest täpselt andnud pole. Näiteks kui viie vastaja kuusissetulekud on 550 €, 600 €, 700 €, 850 € ja 900 €, siis on keskmiseks sissetulekuks (550+600+700+850+900)/5=720 €, mida tegelikult ükski meie vastajatest täpse summana ei saanud.
Aritmeetilise keskmise kasutamise plussiks on see, et ta on lugejale tavaliselt küllaltki hästi mõistetav statistiline näitaja. Selle kasutamisel on aga ka ohte. Keskmisel on sisuline tähendus vaid siis, kui tunnus, mille põhjal ta välja arvutati, on arvuline. Näiteks ei oleks tõlgendatav keskmine perekonnaseis väärtusega 2,6, kui skaala on 0 – vallaline, 1 – vabaabielus, 2 – abielus, 3 – lahutatud, 4 – lesk.
Keskmise kasutamine on problemaatiline järgmistel juhtudel.
- Vastajate hulgas on erindeid ehk tavapärasest väga palju erineva vastuse andjaid. Sellisel juhul on keskmine kallutatud erindi suunas. Kui nt eelmises näites oleks viimase vastaja sissetulek olnud 900 € asemel 9000 €, oleks keskmine sissetulek grupis olnud 2340 €. See summa ei iseloomustaks nimetatud inimeste gruppi kuigi hästi.
- Vastajate seas on tunnuse väärtuse poolest selgelt eristuvad grupid. Sellisel juhul näitab keskmine küll üldist vastust kogu grupi kohta, kuid see ei pruugi olla iseloomulik ühelegi alamgruppidest. Näiteks vaatame sissetulekuid kahes järgmises grupis:
- mehed: 800 €, 900 €, 1100 €;
- naised: 400 €, 600 €, 700 €.
Üldine keskmine kahe grupi peale kokku oleks 750 €, mis poleks tüüpiline vastus kummaski grupis. Paremini iseloomustaks vaadatud kogumit see, kui leida keskmised kummagi grupi jaoks eraldi. Sel juhul oleks meeste keskmine sissetulek 933 € ning naistel 567 €.
3. Vastuste jaotus ei ole sümmeetriline.
Juhul kui esineb eelnimetatud probleeme, võiks kaaluda keskmise asemel mediaani kasutamist.
Standardhälve iseloomustab vastuste hajuvust keskmise ümber. Standardhälbe saab, kui leida kõigi vastajate vastuste erinevus üldisest keskmisest ning arvutada nende erinevuste keskmine. Seega näitab standardhälve tüüpilist erinevust üldisest keskmisest. Kui standardhälve on suur, siis võib arvata, et vastajate vastused on enamasti üldisest keskmisest kaugel. Kui standardhälve on väike, siis on vastajate vastused antud üldise keskmise lähedale. Viimasel juhul tundub, et vastajad on olnud oma vastustes küllaltki üksmeelsed.
Standardhälbe arvutamise valemKui uuritud inimeste vastused on üksteisest väga erinevad ja tunnuse standardhälve on suur (nt üks väga kõrge sissetulekuga vastaja suhteliselt väikeses uuritute grupis), võib aritmeetilise keskmise kasutamine olla problemaatiline.
Dispersioon on standardhälbe ruut. Seda kasutatakse tunnuse hajuvuse iseloomustamiseks nagu standardhälvetki.
Mediaan on punkt tunnuse väärtuste järjestatud skaalal, millest suuremaid ja väiksemaid väärtusi on ühepalju. Seega, järjestades nt vastajate sissetulekud kasvavasse ritta, on mediaaniks selle vastaja sissetulek, kellest suurema ja väiksema sissetuleku teenijaid on ühepalju (ehk kellest reas mõlemas suunas on sama palju vastajaid). Näiteks sissetulekute ridades
550 €, 600 €, 700 €, 850 € ja 900 €
ning
550 €, 600 €, 700 €, 850 € ja 9000 €
on mõlemal juhul mediaaniks 700 €. Sellest tulenevalt sobib mediaani kasutada ka siis, kui vastuste seas on erindeid (ehk teistest väga palju erinevate vastustega indiviide).
Mediaani saab leida arvuliste või järjestustunnuste puhul.
Kvantiilid jagavad tunnuse väärtuste järjestatud rea teatud arvuks võrdseteks osadeks. Sagedamini kasutatavad kvantiilid on detsiilid, kvintiilid ja kvartiilid.
Detsiilid jagavad tunnuse väärtuste järjestatud rea kümneks võrdseks osaks, seega detsiile endid saab leida üheksa, nt esimene detsiil eraldab 10% kõige madalamatest tunnuse väärtustest.
Kvintiilid jagavad tunnuse väärtuste järjestatud rea viieks võrdseks osaks, kvintiile saab leida neli ja esimene kvintiil eraldab ühe viiendiku ehk 20% kõige madalamatest tunnuse väärtustest.
Kvartiilid jagavad tunnuse väärtuste järjestatud rea neljaks võrdseks osaks, kvartiile saab leida kolm ja alumine kvartiil eraldab ühe neljandiku ehk 25% tunnuse kõige madalamatest väärtustest. Järgmine kvartiilidest eraldab teise neljandiku ehk kokku 50% (seega langeb kokku mediaaniga). Ülemine kvartiil eraldab ühe neljandiku ehk 25% tunnuse kõige kõrgematest väärtustest (ehk 75% tunnuse kõige madalamatest väärtustest).
Näiteks vastajate sissetulekute järjestatud reas
400 €, 500 €, 550 €, 600 €, 700 €, 750 €, 850 €, 900 €, 1000 €, 1200 €
on alumiseks kvartiiliks 550 € ning ülemiseks kvartiiliks 900 €.
Mood on vastuste seas kõige sagedamini esinev väärtus. Näiteks kui vastajate sissetulekud on
600 €, 600 €, 700 €, 850 € ja 900 €, siis on moodiks 600 €, mida esines kaks korda (ülejäänud vastusevariante esines vaid korra). Moodi saab leida nii arvuliste, järjestus- kui nominaaltunnuste puhul. Näiteks kui vastajate seas oli kolm naist ja kaks meest, siis soo tunnuse moodiks on vastusevariant „naine“.
Vaatame kirjeldava statistika leidmist analüüsipaketi SPSS abiga (versioon 20).
Avage andmestik ess12eesti.sav (tegemist on tükiga Euroopa Sotsiaaluuringu andmestikust aastast 2012)
Kirjeldava statistika leidmiseks on SPSSis mitu võimalust.
Valdav osa kirjeldava statistika vahenditest tuleb menüüst Analyze – Descriptive Statistics
1) Analyze – Descriptive Statistics – Frequencies
Menüüst „Frequencies“ on võimalik tellida sagedustabeleid ning lihtsamat kirjeldavat statistikat (vt joonis 1).
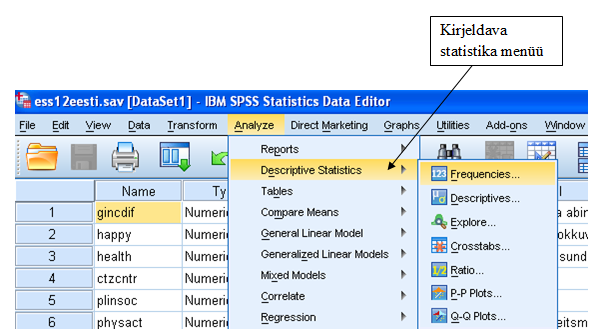
Tellimisaknas „Frequencies“ kirjeldava statistika tellimiseks tuleb esmalt valida tunnus(ed) (praeguses näites „Koht ühiskonnas“) ning saata see/need nooleklahvile vajutades parempoolsesse tellimisaknasse (vt joonis 2), seejärel valida nupu „Statistics“ alt soovitavad kirjeldava statistika näitajad (vt joonis 2 ja 3).
Märge „Display frequency tables“ näitab, et tellitakse ka tunnuse sagedustabel.
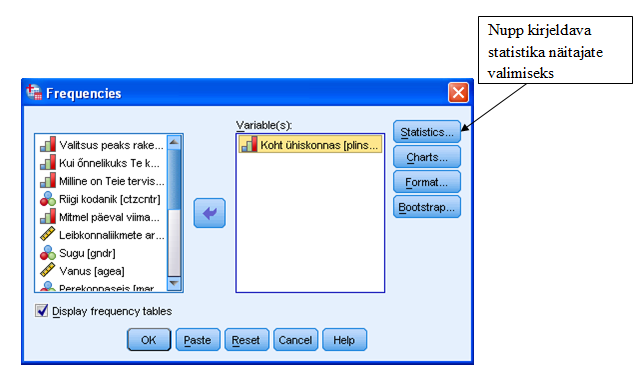
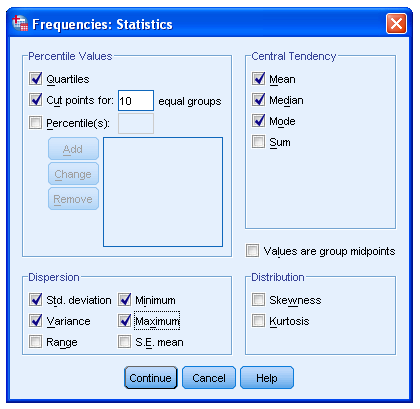
Näites on statistilistest näitajatest valitud
kvartiilid („Quartiles“)
detsiilid („Cut points for 10 equal groups“)
aritmeetiline keskmine ehk keskväärtus („Mean“)
mediaan („Median“)
mood („Mode“)
standardhälve („Std. deviation“)
dispersioon („Variance“)
väikseim esinenud väärtus („Minimum“)
suurim esinenud väärtus („Maximum“)
Selle tulemusena saadakse järgnev väljund aknasse „Output“ (vt tabel 2).
Tabel 1. Kirjeldav statistika tunnuse „Koht ühiskonnas“ kohta, andmestik ess12eesti.sav
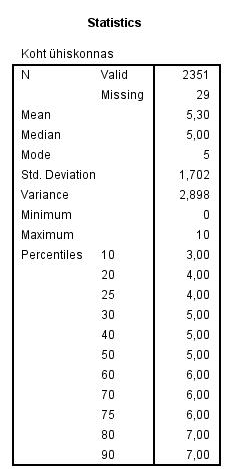
Esimesest tabelist (tabel 1) pealkirjaga „Statistics“ saame teada, et hinnangu enda kohale ühiskonnas on andnud 2351 vastajat. Küsimusele ei oska vastata 29 inimest (nendel on andmestikus „Missing“ ehk puuduv väärtus).
Keskmine hinnang enda kohale ühiskonnas on olnud 5,30 punkti (tunnus on mõõdetud skaalal 0–10, kus 0 tähendab kõige madalamat ühiskondlikku klassi ja 10 kõige kõrgemat). Mediaaniks on 5, seega umbes pooled vastajatest on andnud enda positsioonile ühiskonnas kõrgema ja pooled madalama hinnangu kui 5 punkti.
Mood ehk kõige sagedamini esinev tunnuse väärtus on 5 punkti.
Standardhälve on 1,702 ja dispersioon 2,898 punkti.
Minimaalne esinenud väärtus on 0 ja maksimaalne 10 punkti.
Järgnevad detsiilid ja kvartiilid, mille juures väärtuse 10 taga olev 3,00 tähendab, et 10% vastajatest andis enda koha hinnanguks 3 punkti või vähem. Seega on tegemist kõige alumise ehk esimese detsiiliga.
Alumine kvartiil on 4,00 punkti ning ülemine kvartiil 6,00 punkti.
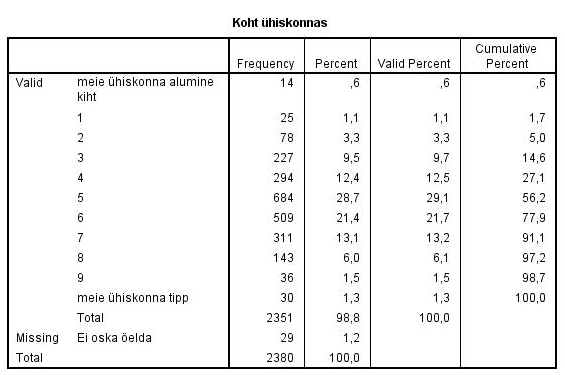
Järgnevas sagedustabelis (tabel 2) on antud tunnuse „Koht ühiskonnas“ sagedustabel. Selgub, et kõige alumisse kihti (0 punkti) on end paigutanud 14 vastajat ning ühiskonna tippu (10 punkti) 30 vastajat. Kõige rohkem vastajaid (684) on valinud vastusevariandi 5 punkti, mis on selle tunnuse puhul moodiks.
Lisaks toorsagedusele („Frequency“) on tabelis esitatud veel protsent kõigist inimestest („Percent“) ning protsent nendest, kes on küsimusele andnud mittepuuduva väärtuse („Valid percent“). Viimases veerus esitatakse kumulatiivne ehk kogunev protsent.
Tabel 2. Sagedustabel tunnuse „Koht ühiskonnas“ kohta, andmestik ess12eesti.sav
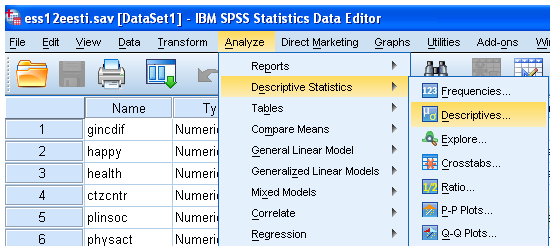
2) Analyze – Descriptive Statistics – Descriptives
Teine võimalus kirjeldava statistika tellimiseks on käsuga „Descriptives“ (vt joonis 4).
Tellimisaknas tuleb valida tunnus(ed), praeguses näites on see „Koht ühiskonnas“ (vt joonis 5).
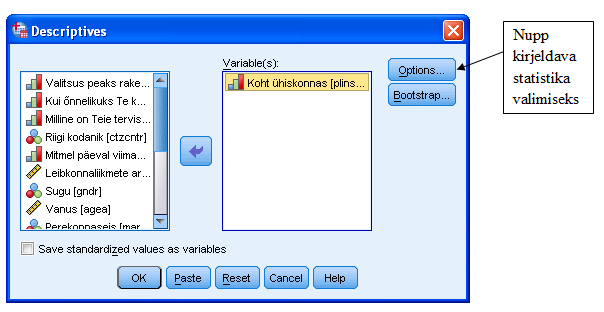
Nupu „Options“ alt saab valida soovitavad statistilised näitajad (vt joonised 5 ja 6).
Praeguses näites on valitud keskmine („Mean“), standardhälve („Std. deviation“), minimaalne („Minimum“) ja maksimaalne („Maximum“) väärtus.
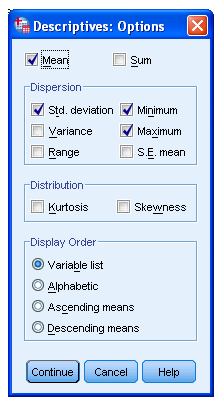
Tulemused on esitatud järgmises väljundis („Output“), vt tabel 3.
Tabel 3. Kirjeldav statistika tunnuse „Koht ühiskonnas“ kohta, andmestik ess12eesti.sav

Vastajate arvuks on 2351. Minimaalne esinenud väärtus oli 0 ja maksimaalne 10 punkti. Keskmine hinnang kohale ühiskonnas oli 5,30 punkti ja selle standardhälve 1,702 punkti.
Järgnevas näites vaatame paketi Excel võimalusi kirjeldava statistika leidmiseks. Näide on üles ehitatud ingliskeelsete menüüdega Exceli baasil.
Avage andmestik ess12eestiexcel.xls
Kirjeldava statistika leidmiseks on Excelis mitu võimalust. Üksiku tunnuse puhul võib kasutada funktsioonide loetelus pakutud valikuid („Insert Function“)
Näiteks kirjutades lahtrisse (või valides „Formulas – Insert Function“):
=AVERAGE(A1:A10) leitakse keskmise väärtus lahtrite A1 kuni A10 põhjal
=STDEV(A1:A10) leitakse standardhälve lahtrite A1 kuni A10 põhjal
=VAR.S(A1:A10) leitakse valimi dispersioon lahtrite A1 kuni A10 põhjal
=MEDIAN(A1:A10) leitakse mediaan lahtrite A1 kuni A10 põhjal
=MODE.SNGL(A1:A10) leitakse mood lahtrite A1 kuni A10 põhjal
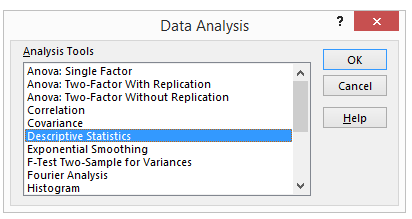
Teise võimalusena saab kasutada kirjeldava statistika moodulit (vt joonis 1)
Data – Data Analysis – Descriptive Statistics
Juhul kui moodul pole aktiveeritud, saab selle aktiveerida järgnevalt.
Näiteks soovides leida kirjeldava statistika tunnuse „Koht ühiskonnas“ kohta, on vaja tellimisaknas andmete asukohaks valida veerg E (tunnuse „Koht ühiskonnas“ asukoht) ning andmestiku pikkuse järgi valitakse 231 andmerida (vt joonis 2).
Järgnevalt saab määrata, kas tunnused on grupeeritud veergudesse („Columns“, nagu praeguses andmestikus) või ridadesse („Rows“).
Märge „Labels in first row“ annab teada, et valitud andmevahemiku esimesel real asub tunnuse nimi.
Alajaotus „Output options“ võimaldab saadavad tulemused paigutada
- ettemääratud aadressiga lahtrist edasi alla ja paremale („Output Range“);
- uuele töölehele („New Worksheet Ply“);
- uude tööraamatusse („New Workbook“).
Märge „Summary statistics“ annab meile tunnuse kohta kokkuvõtva statistika.
Märge „Confidence Level for Mean“ annab usaldusvahemiku.
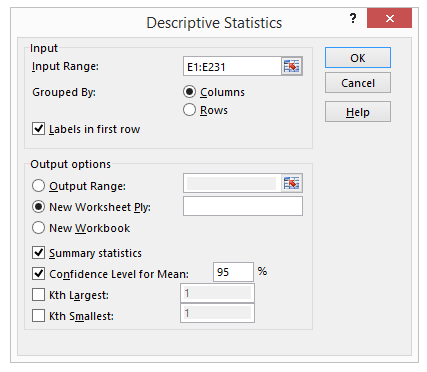
Tellimisaknas (joonis 2) tehtud valikud annavad tulemuseks järgmise tabeli (tabel 1).
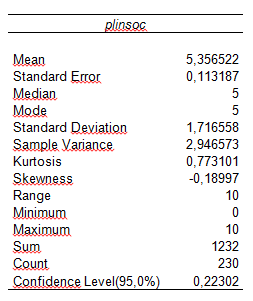
Mean – keskmine
Standard Error – standardviga
Median – mediaan
Mode – mood
Standard Deviation – standardhälve
Sample Variance – dispersioon
Kurtosis – ekstsess
Skewness – asümmeetriakordaja
Range – väärtuste vahemik, miinimumi ja maksimumi vahe
Minimum – minimaalne esinenud väärtus
Maximum – maksimaalne esinenud väärtus
Sum – kõigi väärtuste summa
Count – väärtuste (vastajate) arv
Confidence Level – usaldusvahemiku laius
Tunnuse sagedusjaotused
- Tunnuste sagedusjaotused esitatakse enamasti tabelites ja joonistel protsentide või vastajate arvudena.
- Teksti sees tuuakse välja vaid järelduse seisukohalt kõige iseloomulikumad arvud.
- Sama järelduse kohta pole vaja esitada mõlemat, tabelit ja joonist, vaid piisab ühest.
- Lühema skaalaga tunnuste info võib kirjutada lahti teksti sees.
- Ümardamine: ei pea andma rohkem komakohti, kui on kaetud vaatlusaluste isikutega.
- Küsimuse sõnastus ankeedis ei pea tingimata olema kõigis tabelites/joonistel täpselt välja toodud. Vajadusel võib tekstile lisada eraldi tunnuste kirjelduse osa.
Kirjeldav statistika
- Üksikud keskmised/mediaanid vms esitatakse enamasti teksti sees.
- Tihtipeale antakse koos keskmisega ka standardhälve ja/või vastajate arv ja/või usalduspiirid.
- Ümardamise reeglid sõltuvalt vastajate arvust, mitte rohkem kui 1-2 kohta pärast koma.
- Kirjeldava statistika esitamisel tuleks järgida sama stiili: koma/punkti kasutus, ümardamise ulatus.
- Kasutatud lühendid tuleb lahti seletada esimesel kasutuskorral.
Näide 1
Keskmine hinnang valitsuse tegevusele oli madal (keskmine 4.2, standardhälve 2.5 punkti)
(m=4.2, sh=2.5)
(M=4.2, SD=2.5)
Keskmine hinnang valitsuse tegevusele oli 4.2 punkti (standardhälve 2.5).
Näide 2
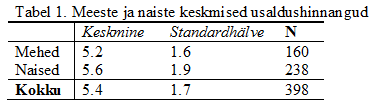
Tooding, L.-M. (2007). Andmete analüüs ja tõlgendamine sotsiaalteadustes. Tartu: Tartu Ülikooli Kirjastus.
Internetimängud kirjeldava statistika kohta:
Rossman/Chance Applet Collection


