Sotsiaalse Analüüsi Meetodite ja Metodoloogia õpibaas
Sissejuhatus klasteranalüüsi
Paketi SPSS enamlevinud meetodid
Liina-Mai Tooding
2020
Mis on klasterdus?
Klasteranalüüs on nimetus suure andmeanalüüsi meetodite kogu jaoks, mille eesmärgiks seatakse objektide rühmitus viisil, kus ühe ja sama rühma liikmed on üksteisele mingis mõttes lähemal kui teise rühma liikmetele. Objektiks ehk indiviidiks võib olla mis tahes füüsiline või loogiline üksus: inimene, hoone, riik, kooliklass, tunnus, kontseptsioon. Objekte kirjeldatakse nende omaduste – klasterdustunnuste – kaudu, mis võivad põhimõtteliselt olla klasterdusmeetodeid varieerides mis tahes formaalset ja statistilist tüüpi: arvulised, järjestusega või nominaaltunnused, pidevad või kategoriaalsed. Eesmärgid, mille puhul klasteranalüüs ette võetakse, võivad samuti olla erisugused: rühmitamine, tüpoloogia loomine, eristustunnuste väljaselgitamine jm. Kaugust ja lähedust objektide vahel iseloomustatakse samuti erisuguselt, nagu näeme allpool. Lõpuks erinevad ka arvutusalgoritmid, mille kohaselt koostatakse vastav tarkvara (ilma selleta on klasteranalüüs mõeldamatu). See kõik kokku tähendab, et klasteranalüüs, mille ideestik kerkis esile 1930. aastatel, on tänaseks päevaks arenenud väga suure variatiivsusega matemaatiliselt põhjendatud metoodikaks. Üks oluline arenguhüpe jääb 1960.–1970. aastatesse, mil (suur)arvutite kasutus laienes praktiliselt kõigile uurimisaladele, ja teine lähiminevikku, mil kerkis esile „suurandmete“ idee, taas tänu arvutikasutuse ja interneti uuele levikulainele võimsate väikearvutite ilmudes. Klasteranalüüs kui mitmeste optimeerimiseesmärkidega metoodika on tugevalt seotud tehnoloogilise alusega. Tähtsateks klasteranalüüsi rakendusaladeks võib pidada statistilist andmeanalüüsi kõikvõimalikel elualadel ja andmekaevet.
Mis on klaster? Kõige üldisemalt öeldes: objektikogum. Edasine täpsustus oleneb meetodist (mudelist), mis on võetud klasterduse aluseks. Nimetame siin sagedamini kasutatavaid üldisemaid põhimõtteid, mida ka allpool, tarkvara kaasates, lähemalt käsitleme. Oluline on seejuures arvestada, et klaster on mitmemõõtmeline objekt, st selle loomise aluseks on mitmest tunnusest (sageli paljudest tunnustest) koosnev andmestik. Klasterdustunnuste valik määrab klastri tähenduse ja lisab veelgi tulemuste varieerimise võimalusi.
Laialt levinud on kaugusepõhine klastrite moodustamine. See tähendab objektidevaheliste ja (juba moodustatud) objektirühmade vaheliste võimalike suhete kasutamist, et otsustada klastrikuuluvuse üle. Kauged objektid on eraldi klastreis ja lähedased ühes. Kaugus võib tähendada ka mittesarnasust ja lähedus sarnasust mingi kriteeriumi alusel. Sellisel põhimõttel toimivad allpool käsitletavad hierarhilised klasterdusmeetodid.
Teine laialt kasutusel olev klasterdustüüp põhineb mitmemõõtmelise klastrikeskmise (tsentroidi, k-keskmise, k viitab mitmemõõtmelisusele) mõistel. Otsitakse klasterdust, mille korral etteantud arvu klastrite puhul on klastrisisesed ruutkaugused klastrikeskmisest minimaalsed. See on rohkete variatsioonidega protseduuride rühm, mida tuntakse k-keskmise klasterdusena.
Nimetame veel otseselt statistilise iseloomuga klasterdust, kus ühte klastrisse kogutakse tõenäoselt ühe ja sama statistilise jaotusega objektid, ja klasterdust võimalikult „tihedate“ mitmemõõtmelise ruumi osade eritlemise nimel.
Mis kohal on klasterdamine andmeanalüüsis? Siin valitseb suur loominguline ja rakendusalati erinev variatiivsus: eritleda tüübid (nt isiksuse psühholoogias), teha kindlaks rühmi eristavad tunnused ja uurida nende eristusvõimet (klassifitseerimine), luua klastrikuuluvuse tunnus sotsiaalse indeksina, jaotada kogum homogeenseteks alaosadeks jpm. Homogeensete alakogumite loomine tähendab suure mitmekesise andmekogumi teatud viisil põhjendatud „tükeldamist“, et statistilised kokkuvõtted oleksid enam asjakohased (nt üldkeskmine, soov eristada jaotuste segu üksikjaotusi). Andmekaeve eesmärki määratletakse üldiselt kui mustrite leidmist andmeis ja jaotus klastreiks tähendab samuti mustri esiletoomist.
Mis on klasterduse lähteks? Eelkõige uurimisülesanne ja selle aineteoreetiline alus, aga ka väljavalitud tunnused, mille asjakohasuse ja komplektsuse eest ülesande seisukohalt vastutab uurija. Lähteks on ka hea kirjeldav info klasterdustunnuste kohta (jaotused, tunnuste omavaheline seos) või mõne eelneva analoogilise uuringu käigus selgunud eelteave klastriteks jagunemise kohta (klastrite oletatav arv, väiksema pilootandmestiku klasterdus).
Mis on klasterduse tulemuseks? Eripära eirates võiks öelda, et klasterdus tähendab klastreid ja suhete osutamist nende vahel: üksteise katvuse poolest (klastrid ei pruugi olla objektide ühisosata), sisalduvuse poolest üksteises (klastrite hierarhia) jm mõttes. Tulemust iseloomustab alati ka subjektiivsus, sest valikuvõimaluste rohkuse tõttu klasterdusülesande püstitamisel, lahendamisel ja lahendi tõlgendamisel on uurijal väga suur voli. Eri klasterdusmeetodid võivad anda vaid osaliselt kokku langevaid klasterdusi ja „tõelisest“ rühmitusest võiks kõnelda nende kokkulangevate osade alusel. Enamasti on arvutiprogrammides ette nähtud võimalus klasterdustulemuse edasiseks kaasamiseks analüüsi sel teel, et igale objektile määratakse klastrikuuluvus andmestiku uue tunnusena, mille analüüs toimub tavapärasel viisil. See on koht, kus uurija lisaks tehnilistele oskustele klastreid moodustada peab rakendama erialapädevust uuele tunnusele sisulise tähenduse andmisel.
Klasteranalüüsil ei ole olemas „õiget“ lahendust. Väliste näitajate kaudu või ekspertotsuse alusel saab vahel, kui objektide kohta on teada tausta- või lisaandmeid, hinnata tekkinud klasterduse tõepära ja klasterduse sisehindamise teel iseloomustada klastrite seesmist ühetaolisust. Selleks on kasutusel suur hulk erinevaid kordajaid – nii suur hulk, et nende vahelise kooskõla leidmine on omakorda ülesanne (vt nt Desgraupes). Klasterdust on vahel kasulik valideerida andmestiku juhuslike lõigete alusel. Klasteranalüüs on lahenduse mitmesusele vaatamata või hoopis tänu sellele rikas ideede allikas konkreetse andmestiku tundmaõppimisel.
Klasteranalüüsi ulatuslikkust piirame käesolevas sissejuhatuses praktika kriteeriumi kohaselt ja tutvustame osa neist mõisteist ja meetodeist, mis on realiseeritud suuremates professionaalsetes laialt levinud statistikapakettides (SAS, SPSS, Stata, Statistica). Klasteranalüüsi tarbeks on loodud ka hulk eriprogramme, sh vabavara, aga ka nendega töötamisel võiks olla kasu „suurte“ lähenemisviisi tundmisest. Lisame veel, et siinkohal me ei ammenda oma sissejuhatavate selgitustega kaugeltki kõiki võimalusi klasterdamiseks, mis on neljas nimetatud paketis.
Kaugus objektide vahel
Kauguse (ik distance) ja sarnasuse (ik similarity) mõõdikuid on praktikas kasutusel ohtrasti. Nende seas orienteerumiseks lähtume klasterdustunnuste tüübist. Enamasti on kaugusmõõdud defineeritud üht ja sama tüüpi tunnuste korral, sh valdavalt kas arvtunnuste või dihhotoomsete tunnuste jaoks. Tuntud võte on nominaaltunnuse (kategoriaalse tunnuse) esitus dihhotoomsete indikaatorite (ik dummy variables) kaudu, mis tähendab, et ka nominaaltunnused on kaugustega kaetud. Järjestustunnuste puhul võiks kaaluda võimalust nende tõlgendamiseks arvulistena, eeldades ühetaolist meetrikat (ühesuurusi tähenduslikke vahesid astmete vahel) või nominaaltunnustena. Eri tüüpi tunnuste kombineerimise ideed ühes kaugusmõõdus kohtab harva. Küll aga leidub algoritme, kus klasterdustunnustena saab korraga kasutada nii mittepidevaid (kategoriaalseid) kui ka pidevaid tunnuseid.
Kauguse puhul lähtume selle intuitiivsest mõttest. Räpina on Tartule lähemal kui Pärnu, kuid kaugus Pärnusse oleneb sellest, kas mööduda Võrtsjärvest lõuna või põhja poolt, st sellest, kuidas on kaugus määratud. Kauguste liike on andmeanalüüsis kasutusel väga arvukalt (vt üldmulje saamiseks nt Vikipeedia vastava teema sisukorda Category: Similarity and distance measures).
Kaugus määratakse kahe objekti vahel, kusjuures kaugus iseendani on 0. Kaugusi mitme objekti vahel võib korrastada kauguste maatriksiks analoogiliselt korrelatsioonimaatriksiga. Kaugus on enamasti lokaalne, konkreetse ülesande kohane, ei pruugi olla arvuliselt tõkestatud ja võib ulatuda mis tahes arvuni olenevalt kasutatavatest tunnustest ning kauguse arvutusreeglist. Võrreldavuse huvides mõnikord kaugused standarditakse mingil viisil, nt võetakse kauguste maatriksi suurim kaugus võrdseks ühega ja teised vastavalt jagatakse suurima kaugusega. Standarditud kaugused väljendavad objektide lähedusastet suhteliselt (ja ühikuta ka juhul, kui kaugusel on ühik).
Kaugus arvtunnuste alusel
Eukleidiline kaugus. Sageli kasutatavaks kauguseks arvuliste tunnuste korral on eukleidiline ehk linnulennukaugus (ik Euclidean distance, bird’s-eye distance). Olgu kaks indiviidi o1 ja o2 tasandil vastavalt punktides (x1,y1) ja (x2,y2). Joonisel 1 on kujutatud linnulennukaugus d tasandi kahe punkti vahel ja selle arvutus koolikursusest tuttava Pythagorase teoreemi abil. Sellist kaugust üldistatuna mis tahes tunnuste arvule tuntaksegi eukleidilise kaugusena.
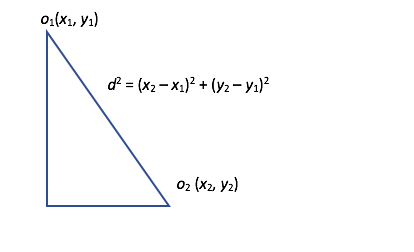
Vaatleme indiviidide paigutust M-mõõtmelises ruumis M erisuguse (võimalik et omavahel seotud) tunnuse alusel. Vaatleme kaht indiviidi o1 ja o2 vastavalt mõõtmistega x11, x12, …, x1M ja x21, x22, …, x2M . Kahe indiviidi vaheline eukleidiline kaugus d(o1,o2) leitakse valemist:
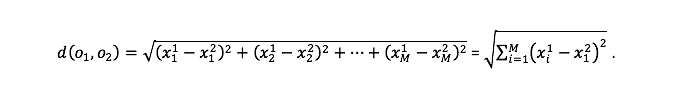Eukleidiline kaugus toetub kõigile tunnustele ühtmoodi, sest kõigi tunnuste ruutvahed liituvad. See tähendab, et tunnused peaksid olema sama suurusjärku, kui tahame, et need osaleksid kauguse määramisel võrdväärselt. Üksiktunnuse alusel leitud vahe võetakse kauguse arvutamisel ruutu, et mitte teha vahet objektide erinevuses märgi alusel. Seejuures ruutu tõstmine võimendab nende tunnuste tähendust, mille korral objektide vahe on suur. Eukleidiline kaugus on sümmeetriline: d(o1,o2) = d(o2,o1). Kasutatakse ka eukleidilist ruutkaugust (ik Squared Euclidean distance), mille puhul eelnevas valemis jäetakse ruutjuur võtmata.
Olgu näiteks kolme objekti mõõtmisel ruumis (nt pikkus, laius, kõrgus) saadud järgmine andmetabel:
o1 1 1 1
o2 2 3 4
o3 2 5 3
Eukleidilised kaugused võimalikus kolmes objektipaaris on järgmised:
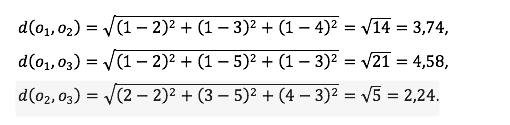
Eukleidilised ruutkaugused on vastavalt 14, 21 ja 5. Mõlema kauguse tüübi alusel on objektid 2 ja 3 teineteisele lähemal kui objektid ülejäänud paarides. Kauguste maatriks on järgmine (sümmeetria tõttu piisab ühest poolest, millele on parema loetavuse nimel lisatud ka diagonaal (vasakpoolne standardimata, parempoolne standarditud suurima väärtuse järgi):
o1 0 o1 0
o2 3,74 0 o2 0,82 0
o3 4,58 2,24 0 o3 1,00 0,49 0
o1 o2 o3 o1 o2 o3
Kordame üle, kui kaugust määravad tunnused on mõõdetud erinevatel skaaladel (on erineva variatiivsusega, erinevat suurusjärku), siis tuleb tunnuseid kauguse arvutamise eel kindlasti standardida ja muuta võrreldavateks. Suurearvuliste väärtustega tunnus (nt töötasu eurodes) ei tohiks kauguse arvutamisel domineerida väikesearvuliste väärtustega tunnuse üle (nt töökogemus aastates). Standardimiseks on mitmeid eri viise, sagedasim neist on skooride arvutamine kogumi keskmise ja standardhälbe suhtes (saadakse väärtused keskmisega 0 ja standardhälbega 1).
Linnakaugus (Manhattani kaugus, plokk-kaugus, ik block distance) kahe objekti vahel on lähedane eukleidilisele kaugusele, kuid vahe märgist vabanemiseks kasutatakse ruutu tõstmise asemel absoluutväärtust, st vaadeldakse absoluutseid hälbeid:
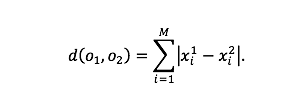
Kõneldes joonisele 1 toetudes, võiks öelda, et mõõdetakse kaugust kolmnurga külgi (kaateteid) mööda, mitte hüpotenuusil. See põhjendab ka nimevalikut, sest linnas liigutakse enamjaolt mööda majaplokkide servi, mitte diagonaalis üle kvartali.
Olgu näiteks kolme objekti mõõtmisel ruumis saadud järgmine andmetabel:
o1 1 1 1
o2 2 3 4
o3 2 5 3
Linnakaugused võimalikus kolmes objektipaaris on järgmised:
do1,o2=1-2+1-3+1-4=6
,
do1,o3=1-2+1-5+1-3=7
,
do2,o3=2-2+3-5+4-3=3
,
ja kauguste maatriksid standardimata (vasakul) ja standarditud kujul on järgmised:
o1 0 o1 0
o2 6 0 o2 0,86 0
o3 7 3 0 o3 1,00 0,43 0
o1 o2 o3 o1 o2 o3
Paaride järjestus kauguse alusel on sama nagu eukleidilise kauguse puhul, aga paarisisesed kaugused on suuremad kui eukleidilise kauguse puhul. Ka linnakauguse puhul on vajalik tunnuste standardimine, kui soovime nende ühetaolist mõju kauguse kujunemisele.
Korrelatiivne kaugus põhineb kahe objekti vahelisel korrelatsioonikordajal. Oleme harjunud, et tavaliselt uuritakse kahe tunnuse vahelist korrelatsiooni ja selle aluseks on kahe tunnuse individuaalsed väärtused kõigi objektide/indiviidide korral. Objektidevahelise korrelatsiooni arvutamise aluseks on analoogselt sellele kummagi objekti/indiviidi individuaalsed väärtused klasterdamiseks võetud tunnuste korral, st tunnused ja objektid/indiviidid on mõtteliselt oma kohad vahetanud. Kui vaadelda kaht tunnust, siis positiivse objektidevahelise korrelatsioonseose korral, kui ühe objekti väärtus ühel tunnusel on suurem kui teisel, on see keskmiselt nõnda ka teise objekti korral. Positiivne tugev korrelatsioonseos objektide vahel peegeldab objektide tunnuste alusel arvestatavate profiilide sarnasust, negatiivne tugev korrelatsioonseos – olukorda, kus üks profiil on teise suhtes „otse vastupidine“ (suurele tunnuse väärtusele ühel objektil vastab väike teisel tunnusel ja väiksele suur). Näiteks kahe õpilase vaheline korrelatsioonseos põhiainete hinnete profiilide alusel on positiivne siis, kui neil on ühtedes ja samades ainetes paremad ja ühtedes ja samades ainetes halvemad hinded.
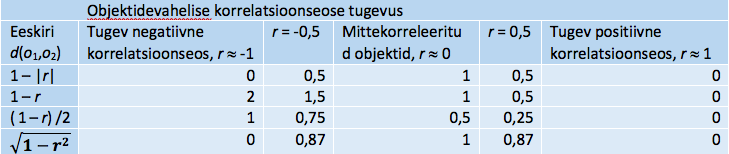
Olgu r(o1,o2) = r kahe objekti vaheline korrelatsioonikordaja. Korrelatiivse kauguse arvutamiseks kasutatakse mitmeid erisuguseid eeskirju, millest näitena mõnesid iseloomustame tabelis 1 (tabeli neljas reas neli erinevat korrelatiivset kaugust). Esimene ja viimane kaugus peegeldavad objektide lähedust ainult korrelatsioonseose tugevuse alusel, märgist olenemata. Nende puhul on kaugus mittekorreleerituse (r = 0) olukorra suhtes sümmeetriline, aga märki arvestavate definitsioonide korral ei ole (vrd kaugusi -0,5 ja 0,5 korral). Viimane tabelis toodud kaugus sõltub korrelatsioonikordajast mittelineaarselt.
Sarnasusmõõdud mittearvuliste tunnuste korral
Sarnasuskordajad sagedustabeli alusel võimaldavad uurida objektivahelist kaugust dihhotoomsete tunnuste puhul. Dihhotoomsete indikaatorite rühmana saab esitada ka iga nominaaltunnust (ühe võrra vähem indikaatoreid kui on nominaaltunnusel mitteolemasolu alusel, ik dummy variables).
Vaatleme kahe objekti (nt isiku) o1 ja o2 kohta M dihhotoomse tunnuse alusel moodustatud sagedustabelit (tabel 2) väärtustega 0 ja 1 (nt 1 – osales üritusel , 0 – ei osalenud, vaatluse all M üritust ehk juhtu).
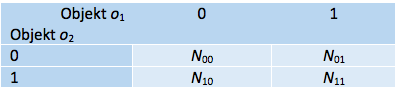
Sagedus N11 näitab ühtivuste arvu kahel objektil vaadeldava nähtuse olemasolu/esinemise alusel (mõlemal isikul väärtus 1, nt N11 üritusel osalesid mõlemad) ja N00 mitteolemasolu alusel (nt N00 üritust olid sellised, kus kumbki isikuist ei osalenud). Sagedused N01 ja N10 näitavad mitteühtivuste arvu, kui ühel objektil nähtus esineb ja teisel mitte. Mida enam on ühtivusi, seda sarnasemad on objektid, mida enam mitteühtivusi, seda mittesarnasemad (kaugemad) on objektid. Kaugus kahe objekti vahel arvutatakse tabelisageduste kaudu, kusjuures kasutusel on palju erinevaid arvutusreegleid. Toome mõned näited sellisel teel saadud kaugustest ja sarnasuskordajatest.
Jaccardi sarnasuskordaja (ik Jaccard similarity coefficient):
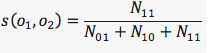
võtab arvesse ühtivuste arvu olemasolu alusel (mõlemal on ürituse kohta üheaegselt jaatav vastus) ja suhestab selle võimaluste üldarvu, millest on välja jäetud ühtivuste arv mitteolemasolu alusel (mõlemal objektil on eitav vastus). Mida suurem on jaatuste arv korraga mõlemal, seda sarnasemad on objektid (näites: mõlemad võtsid osa samadest üritustest). Arvu N00 kõrvalejätmine on põhjendatud, et vältida sarnasuse tugevdamist mitteesinemise arvelt, kuigi millegi üheaegne puudumine on ka sarnasus. Võimalikud väärtused on 0 (üheaegseid jaatavaid vastuseid ei ole) kuni 1 (kõik vastused on üheaegselt jaatavad).
Lihtne ühtivuskordaja (ik simple matching coefficient) arvestab mõlemat liiki sarnasust, nii olemasolu kui puudumise mõttes:
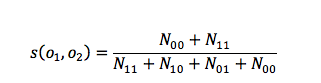
Siin tuleb jälgida, et valitud M tunnust sisaldaksid ühetaolist tähendust kõigi objektide seisukohalt (küsitavaks ürituseks ei sobi nt konkreetne Võrumaa külasimman, küll aga lihtsalt simman, mida võib ette tulla igal pool). Võimalikud väärtused on 0 (ei ole üheaegseid jaatavaid ega eitavaid vastuseid) kuni 1 (kõik vastused on kas üheaegselt jaatavad või eitavad).
Lance’i-Williamsi mittesarnasuse kordaja (ik Lance-Williams dissimilarity coefficient) leiab mitteühtivuste arvu suhte juhtude üldarvu, millest ühtivuste arv mitteolemasolu alusel (üheaegsete eitavate vastuste arv) on kõrvale jäetud, kuid selle asemel kasutatud kahekordselt ühtivuste arvu olemasolu alusel (üheaegselt jaatavate vastuste arvu). Arvutusvalem on järgmine: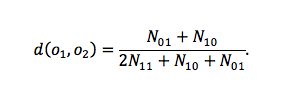
Kordaja muutub väärtusest 0 (mitteühtivusi ei ole) kuni väärtuseni 1 (ühtivusi ei ole).
Yule’i kordaja Q mõõdab assotsiatsiooni neljaväljatabelis (2×2-tabelis) järgmise eeskirja kohaselt:
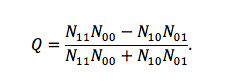
Kui vähemalt üht laadi mitteühtivusi ei ole (st kahe objekti puhul kas varianti „osales-ei osalenud“ või varianti „ei osalenud-osales“ või kumbagi varianti ei esine), siis Q = 1. Kui vähemalt üht laadi ühtivusi ei ole (st kas varianti „osales-osales“ või „ei osalenud-ei osalenud“ või kumbagi varianti ei esine), siis Q = -1. Ülejäänud olukorrad annavad -1 ja 1 vahepealse väärtuse. Siinkohal on kasulik meenutada šansside suhte kordajat (ik odds ratio) e, kus
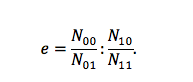
Kui e = 1, st sagedustabeli alusel objektid ei ole seotud, siis N00N11 = N10N01 ja Q = 0.
Yule’i kordaja Y mõõdab assotsiatsiooni neljaväljatabelis samuti piirides -1 kuni 1 ja selle arvutusvalem on sageduste suhtes kordajale Q analoogiline:
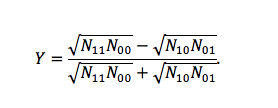
Yule’i kordaja Y avaldub väikeste algebraliste teisenduste järel šansside suhte kordaja kaudu järgmiselt
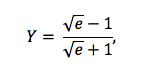
millest nähtub, et objektidevahelise seose puududes (st kui e = 1) on kordaja väärtuseks 0. Vahetult valemist tuleneb, kui vähemalt üht laadi mitteühtivusi ei ole, siis Y = 1. Kui ei ole vähemalt üht laadi ühtivusi, siis Y = -1.
Yule’i kordajad on omavahel seotud valemiga Q = 2Y/(1+Y2).
Paketis SPSS on realiseeritud mitukümmend erinevat kordajat dihhotoomsete tunnuste alusel kauguse, sarnasuse ja erinevuse hindamiseks. Vahe kordajate vahel seisneb sagedustabeli elementide erinevas suhestamises (vt nt Distancies …, Choi jt 2010).
Tabelis 3 on Euroopa sotsiaaluuringu kodanikuaktiivsuse tunnusploki eeskujul toodud näide kolme isiku A, B ja C tegevusest, esitatud nendevahelised sagedustabelid ja arvutatud mitmeid kordajaid. Teineteisest kõige kaugemal ja kõige erinevamad on A ja B, kõige sarnasemad – B ja C. Isikute A ja C sarnasuses on ülekaalus sarnasus mitteesinemise („ei“) poolest, mida Jaccard’i ja Lance’i-Williamsi kordajates käsitletakse teistmoodi kui sarnasust esinemise poolest.
Algandmed
Sagedustabelid ja kordajad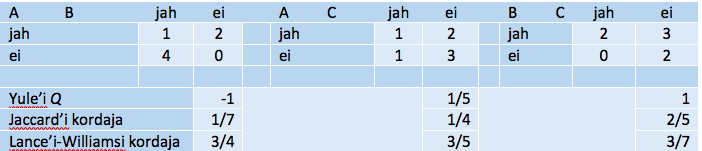
Kauguste arvutamiseks loendustulemuste kaudu on kõige sagedamini kasutusel tavaline hii-ruut-statistik sagedustabeli alusel ja sellest tuletatud standarditud mõõdikud.
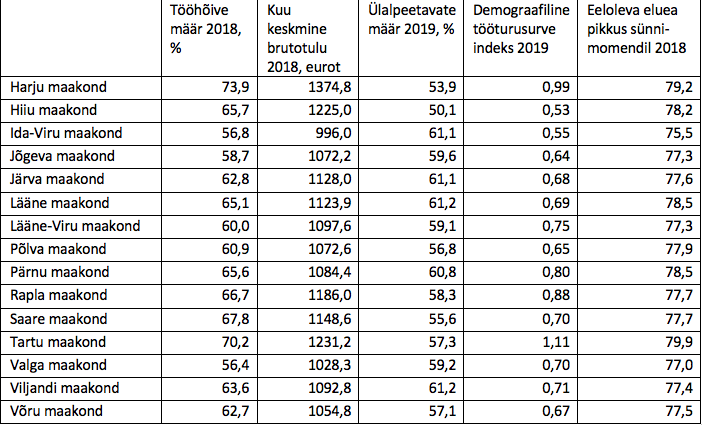
Kauguste arvutamine paketi SPSS abil
Käsurea Analyze – Correlate – Distances järel avanevas aknas teha järgnevad valikud. Et kauguste nimetused ei ole erinevais allikais samad, siis on kasulik alati vaadata programmi juhendmaterjale, (siinkohal: Distances. IBM Knowledge Center … ).
Variables – valida tunnused, mille alusel kaugused arvutada.
Label cases by – määrata objektide nime tunnus, kui see on andmestikus olemas.
Compute distances – märkida, kas leida kaugused indiviidide vahel (Between cases, andmestiku read) või tunnuste vahel (Between variables, andmestiku veerud).
Measure – valida, kas leida kaugused (Dissimilarities) või lähedus- ehk sarnasusmõõdud (Similarities).
Measures – selle sildi alt saab valida tunnusetüübile vastavad kaugus- ja sarnasusmõõdud.
Valik Dissimilarities. Vahemikskaala (Interval, arvskaala) korral on võimalik kasutada:
eukleidilist kaugust (Euclidean distance),
eukleidilist ruutkaugust (Squared Euclidean distance),
Tšebõševi kaugust (Chebyshev distance), kauguseks objektide väärtuste vahe absoluutväärtuse maksimum,
linnakaugust (Block distance),
Minkowski kaugust (Minkowski distance), eukleidilise kauguse üldistus, kus ruututõstmise asemel kasutatakse etteantud astet ja sellele vastavalt ka ruutjuure asemel vastavat juurt,
kasutaja enda defineeritud kaugust (Customized).
Valik Dissimilarities. Loendustulemuste (Count) alusel saab kaugust hinnata hii-ruut-statistiku abil (Chi-square measure) või selle standardimisel phi (fii)-statistiku abil (Phi-square measure).
Valik Dissimilarities. Dihhotoomsete (binaarsete, Binary) tunnuste alusel saab kasutada eukleidilist kaugust (Euclidean distance), eukleidilist ruutkaugust (Squared Euclidean distance), Lance’i-Williamsi kordajat ja mitmeid teisi dihhotoomsete tunnuste neljaväljatabelilt arvutatavaid kordajaid: Size difference, Pattern difference, Variance, Shape. Dihhotoomsete tunnuste puhul tuleb ka osutada, mis koodiga on olemasolu (jaatust) märkiv vastus (Present, vaikimisi 1) ja mis koodiga alternatiiv (Absent, vaikimisi 0).
Valik Similarities. Vahemikskaala tunnuste (Interval) korral on võimalik kasutada
korrelatsioonikordajat (Pearson correlation) traditsioonilises mõttes,
koosinus-mõõtu (Cosine), mis kasutatavate tunnusvektorite geomeetrilise tõlgenduse kohaselt tähendab nendevahelise nurga koosinust (nurk 0 ehk koosinus 1 tähendab ühtelangevust, nurk 90 ehk ristseis tähendab mittesarnasust).
Valik Similarities. Dihhotoomsete tunnuste (Binary) korral on võimalik rakendada 20 erinevat sarnasusmõõtu, millest osa on eespool käsitletud ja ülejäänute puhul tuleks toetuda eespool nimetatud originaaljuhendile. Taas tuleb osutada mis koodiga on olemasolu (jaatust) märkiv vastus (Present, vaikimisi 1) ja mis koodiga alternatiiv (Absent, vaikimisi 0).
Vahemikskaala tunnuste ja loendustulemuste kaugus- ja sarnasusmõõtude korral on võimalik aluseks olevaid tunnuseid käsitleda võrreldavuse suurendamiseks teisendatult. Sildi Transform Values alt saab valida järgmisi viise, kusjuures tuleb näidata, kas teisendada tunnuse piires (By variable) või indiviidi piires (By case):
standardimine keskmise ja standardhälbe suhtes (Z scores),
teisendamine skaalale -1 kuni 1 (Range -1 to 1), iga väärtus jagatakse haardega,
teisendamine skaalale 0 kuni 1 (Range 0 to 1), väärtus, millest on lahutatud vähim väärtus, jagatakse haardega,
teisendamine maksimumi järgi (Maximum magnitude of 1), väärtus jagatakse suurima väärtusega,
teisendamine keskmise järgi (Mean of 1), väärtus jagatakse keskmisega,
teisendamine standardhälbe järgi (Standard deviation of 1), väärtus jagatakse standardhälbega.
Kaugusi ja sarnasusmõõdikuid on võimalik võrreldavuse suurendamiseks standardida järgmiselt (sildi Measures alt valikud Transform Measures):
võtta esialgse väärtuse absoluutväärtus, st loobuda märgist (Absolute values),
paremaks tõlgenduseks vahetada märk, st kauged objektid saavad lähedasteks ja vastupidi (Change sign),
võrreldavuseks standardida skaalale 0 kuni 1 (Rescale to 0–1 range).
Esitame kauguste teema lõpetuseks näite Eesti maakondade vaheliste kauguste kohta, mis on leitud järgmisi tunnuseid arvestades: tööhõive määr 2018, kuukeskmine brutotulu 2018, ülalpeetavate määr 2019, demograafiline tööturusurveindeks 2019, eeloleva eluea pikkus sünnimomendil 2018 (allikas Eesti statistika andmebaas, vastavalt tabelid TT4662, ST004, RV063U, RV06U, RV0452). Võiks öelda, et need tunnused peegeldavad kokkuvõttes maakondade heaolu ja elujõudu. Tunnuseid kasutasime standarditult maakondade keskmise ja standardhälbe suhtes, seega kaugusel ei ole ühikut ja arvud on kasutatavad üksnes selle kauguste maatriksi piires võrdlemiseks. Kauguse tüüp on eukleidiline kaugus.
Näitega soovime rõhutada kauguste maatriksi olulisust ka omaette analüüsi vahendina, kui on vaja mõnd väiksemat objektikogumit kirjeldada. Nii näeme maakondade kauguste maatriksist (tabel 4), et suurim kaugus on Harjumaa ja Ida-Virumaa vahel (kaugus 7,4), aga ka Valgamaa ei ole Harjumaa lähedal. Valitud tunnuste alusel jääb ka Hiiumaa teistest suhteliselt kaugele. Et kasutame sama näidet veel ka edaspidi, siis jätame uurimise, mis viib mõnd maakonda teistest eemale, hilisemaks.
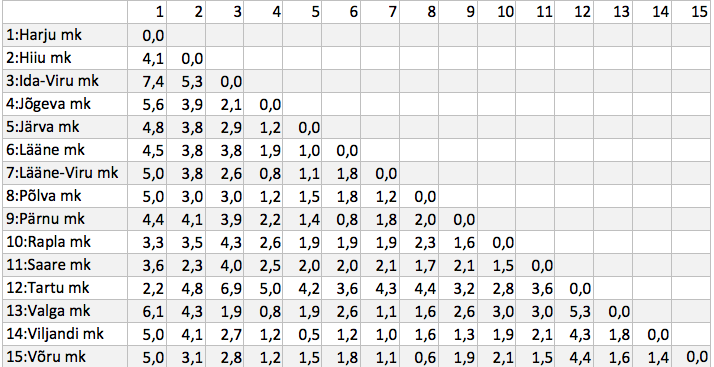
Kauguste maatriks sisaldab huvitavat infot ja väärib omaette analüüsi, nt erindite (teistest silmapaistvalt kaugete objektide) märkamisel, kuid on väga mahukas ja väheülevaatlik. Mida teha? Kauguste maatriksi alusel võiks leida konkreetse objekti keskmisi kaugusi teistest, tuua esile teineteisest kaugeimad ja lähimad objektid jne, teha tavaline andmehulga (andmestikuks kaugused) analüüs. Üks võimalusi oleks paigutada objektid nendevaheliste kauguste alusel parimal viisil teatavasse uude teljestikku (1–2 telge), mis võtavad kokku ja peegeldavad kaugusi ja seega kauguste aluseks olevaid tunnuseid (mitmemõõtmelise skaleerimise idee). Teine võimalus oleks tuletada objektide rühmad klasteranalüüsi teel kaugusi aluseks võttes, mida allpool ka teeme.
Kuidas käsitleda kauguste arvutamisel andmelünki? Väga väheste andmetega objektid võiks kõrvale jätta ja ülejäänute seas kasutada konkreetse objektipaari kohast andmehulka, seda muidugi juhul, kui lünki ei ole palju. Eelnev lünkade „täitmine“ puuduva väärtuse prognoosimise teel muid tunnuseid kasutades on samuti asjakohane.
Hierarhilised klasterdusmeetodid
Hierarhiline klasterdus kujutab endast üksteisega suhestuvate klasterduste jada, millest uurija ise valib sobiva(d) klasterduse(d) ja töötab nendega edasi muude meetoditega. Klasterdused kujunevad sammuviisiliselt, kus klastrite „evolutsioon“ on hästi jälgitav ja võib tõlgenduses anda kasulikku lisainfot. Hierarhiline klasterdusviis on mõeldav väikesemahuliste objektikogumite klasterdamisel, seda eeskätt tulemuste loetavuse huvides, sest arvutuste mahukus, mis klasteranalüüsi algpäevil oli probleem, kujuneb tänapäeval takistuseks alles väga suure objektihulga korral. Tänu ka tulemuste ilmekale graafilisele kujutamisele on hierarhilised meetodid laialt levinud.
Hierarhilised meetodid jagunevad kaheks: ühendavad (ik agglomerative) meetodi ja lahutavad (ik divisible) meetodid, kusjuures lahutavad meetodi on vähem kasutusel. Hierarhilise ühendava klasterdusmeetodi esimesel sammul (hierarhia esimesel tasemel) on iga objekt omaette klaster ja viimasel sammul (hierarhia viimasel tasemel) moodustavad kõik objektid ühise klastri. Igal hierarhia tasemel tehakse üks liigutus klastrite ühendamiseks teatud printsiibi kohaselt. Igal sammul (esimene välja arvatud) on eelmine klasterdus käesoleva klasterduse teatav liigendus. Analoogiliselt on iga klasterdus (viimane välja arvatud) omakorda järgneva teatav liigendus. Hierarhiline lahutav klasterdus tähendab vastupidist – esimesel sammul on kõik objektid ühises klastris ja viimases igaüks eraldi. Tegevus igal sammul tähendab ühe klastri lahutamist. Millised klastrid konkreetsel sammul teisenevad, see oleneb klastritevahelise kauguse valikust, mis omakorda määrab klasterdusmeetodi. Klastrite arvu ette ei pea määrama ja klasterduste analüüsis võib (sh klastrite tõlgendusele toetudes) pakkuda lõpptulemusena mitmeid versioone.
Vaatleme tuntumaid ühendavaid hierarhilisi klasterdusmeetodeid. Neil on ühine see, et igal sammul ühendatakse omavahel kaks klastrit, mille vaheline kaugus on vähim. Meetodeid eristab muuhulgas see, kuidas on määratud klastritevaheline kaugus. Objektidevaheline kaugus tuleb uurijal määrata ülesandest ja klasterdustunnuste iseloomust olenevalt (vt eelnevat, kauguste alaosa käesolevas tekstis). Tunnuste valik meetodi rakendamisel on seejuures samuti sisuline otsus.
Ühe seose meetod ehk lähima naabri meetod (ik single linkage, nearest neighbor method). Kaugus kahe klastri vahel on nende klastrite lähimate elementide vaheline kaugus. Omavahel ühendatakse kõigi võimalike klastripaaride seast need klastrid, mille lähimad elemendid on teineteisele kõige lähemal. Praktikas on meetodile sageli omane ahelaefekt: objekte lisatakse järjest olemasolevatesse klastritesse juurde ja uut klastrit alustatakse vastumeelselt.
Täieliku seose meetod ehk kaugeima naabri meetod (ik complete linkage, furthest neighbor method). Kaugus kahe klastri vahel on nende klastrite kaugeimate elementide vaheline kaugus. Omavahel ühendatakse kõigi võimalike klastripaaride seast need klastrid, mille kaugeimad elemendid on teineteisele kõige lähemal. Täieliku seose meetod arvestab ka objektide paigutust klastri sees ja seega kasutab ära klastrite ühendamisel konkreetsel sammul rohkem teavet kui ühe seose meetod. Kui tegelikult on klastrid küllalt kompaktsed rühmad, siis see meetod avastab need hästi.
Klastritevahelise keskmise kauguse meetod (ik between-groups linkage method, unweighted/weighted pair group method with arithmetic mean, UPGMA, WPGMA). Kahe klastri vaheliseks kauguseks loetakse keskmine kaugus kõigis objektipaarides, mil üks paariline kuulub ühte ja teine teise klastrisse. Omavahel ühendatakse need klastrid, mille puhul selline keskmine kaugus on vähim. Kui on sisuliselt põhjust objekte käsitleda nende tähtsust väljendavate kaaludega, siis arvutatakse kaalutud keskmine kaugus ja vastav meetod on klastritevahelise kaalutud keskmise kauguse meetod.
Klastritesisese keskmise kauguse meetod (ik within-groups linkage method). Kahe klastri vaheliseks kauguseks loetakse keskmine kaugus kõigis objektipaarides, mida saab moodustada klastrite ühendamisel tekkinud objektihulgas. Omavahel ühendatakse need klastrid, mille puhul selline keskmine kaugus on vähim. Kui on sisuliselt põhjust objekte käsitleda nende tähtsust väljendavate kaaludega, siis arvutatakse kaalutud keskmine kaugus ja vastav meetod on klastritesisese kaalutud keskmise kauguse meetod. See klasterdusviis võtab otseselt arvesse ka ühendatavate klastrite seesmist ülesehitust.
Wardi meetod (ik Ward’s method) on kujunenud praktikas hierarhilistest klasterdusmeetoditest soosituimaks ja seda peetakse heaks klastrite äratundjaks. Meetod erineb eelnevas kirjeldatuist ja toetub klastreis arvutatud summaarsetele ruuthälvetele klastrikeskmise suhtes (klastrikeskmise määravad klasterdustunnuste keskmised). Mida väiksem on summaarne ruuthälve, seda „tihedam“ on klaster klastrikeskmise ümber. Omavahel ühendatakse need klastrid, mille puhul summaarse ruuthälbe kasv ühendklastris võrreldes klastritesiseste summaarsete ruuthälvete summaga on vähim. Saab näidata, et see tähendab kaalutud ruutkaugust ühendatavate klastrite klastrikeskmiste vahel (kaal klastrite suuruste kaudu). See ühendamisreegel on loomulik: esimesel sammul on klastri (üksikobjekti) ruuthälve null, iga ühendamisega summaarne ruuthälve kasvab ja hea on, kui kasv on võimalikult väike. Wardi meetod eelistab omavahel ühendada lähendaste klastrikeskmistega klastreid. Kauguseks selle meetodi korral võetakse eukleidiline ruutkaugus (toetub ruuthälbeile).
Hierarhilised klasterdusmeetodid toetuvad erinevatele kriteeriumidele ja seega võivad ka tulemused teatavas ulatuses lahkneda. Mida selgepiirilisem on kogumi jaotus alaosadeks, seda enam on kokkulangevusi eri meetodil saadud klasterdustes.
Vaatleme näidet Eesti maakondade klasterdamisest teatud heaolunäitajate alusel, kasutades sama andmestikku nagu kauguste maatriksi (tabel 4) näites. Tunnuseid käsitleme standarditult tunnuse keskmise ja standardhälbe suhtes, lünklikke objekte jätame kõrvale paarikaupa. Rakendame klasterdamiseks Wardi meetodit ja täieliku seose meetodit eukleidilise ruutkauguse alusel. Klastrinumbrite tunnuse salvestame neljaklastrilise liigenduse kohalt ja toome esile klasterdustunnuste profiili neis neljas klastris.
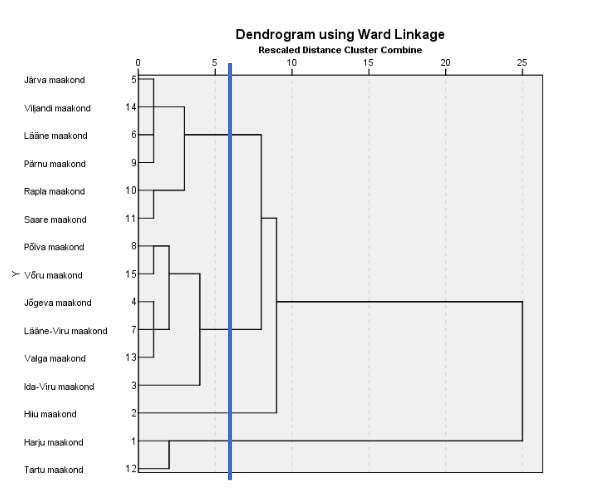
Dendrogrammil näidatakse, kuidas on toimunud järjestikune klastrite liitumine alustades seisust, kus iga maakond moodustab omaette klastri (joonis 2). Selle arvestamiseks, millal klasterduse algusest arvates mingi ühinemine toimub, on antud vasakult paremale kulgev kaugust peegeldav skaala väärtustega 0 kuni 25. Klastrite liitumiskoht kauguse skaalal näitab ka, kui lähedased on üksteisele klastri liikmed teatud sammul (nt Ida-Viru suhteliselt hiline liitumine). Nii näeme, et üheks klastriks ühinetakse lõpus nö jõuga ja kaks klastrit püsib eraldiseisvana kuni lõpuni. Kahjuks tekkis meil liigitus, kus üks klastritest (Hiiu maakonda sisaldav klaster) jääb klasterdusprotsessis pikaks ajaks eraldi ja enne, kui see ühineb suurt hulka maakondi sisaldava klastriga, olid selle ülejäänud liikmed ammu juba ühinenud, seega Hiiumaa on sinna paigutatud formaalselt. Ilmselt oleks mõistlik vaadelda liigituspuud umbes suhtelise kauguse 6 kohalt, kus on moodustunud neli klastrit, kahjuks küll üks klaster üheliikmeline. Rõhutame, et uurija valib ise, mitme klastriga ta töötab, sealhulgas tugevalt subjektiivsete kaalutluste saatel (tõlgenduslikult). Kuidas nimetada klastreid, on vastutusrikas ja hoolikat kaalumist vajav otsus.
Lahendasime sama ülesande veel ka täieliku seose meetodil ja näeme nii ühtelangevusi kui ka erinevusi (joonis 3). Viieklastrilises liigituses näeme üht suuremat maakondade rühma samas koosseisus ja teist ilma Ida-Viru maakonnata. Hiiu ja Ida-Viru maakonnad jäävad eraldiseisvateks ühest elemendist koosnevateks klastriteks. Tartu ja Harju maakonnad on ühinenud nagu Wardi meetodi puhulgi. Neljaklastriline liigitus täieliku seose meetodil ei erista maakondi kuigi hästi.
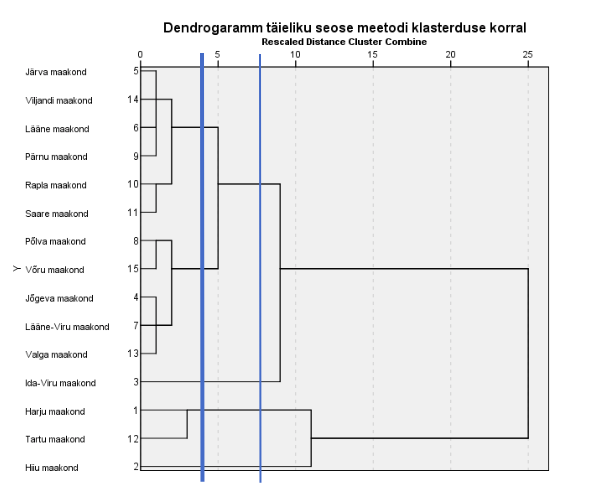
Et paremini näha ühinemise käiku, esitatakse liigitus veel ühel kujul, nimelt omapärase nn jääpurika ehk seina diagrammina (joonis 4), mida tuleb joonisel esitatud kujul vaadelda alt ülespoole. Esialgu on kõik 15 maakonda üksteisest eraldatud valge tulbaga (seinaga). Kohe esimesel sammul kaob sein kahe kõige lähema objekti vahelt (Viljandi ja Järva maakond), seejärel kahe järgmisena lähedaste vahelt (Võru ja Põlva maakond) ja nõnda edasi, kuni kõik maakonnad moodustavad ühe klastri (seinad on kadunud). Klastrite arvu mingil sammul näitab püsttelg. See diagramm on dendrogrammile heaks täienduseks, sest dendrogrammi formaat (eriti suurema indiviidide arvu korral) ei suuda üksteisest eristada lähedasel kauguslävel toimunud ühendamisi. Sama otstarve – liigituspuu täiendamine – on ühendamistabelil (ühendamisplaanil).
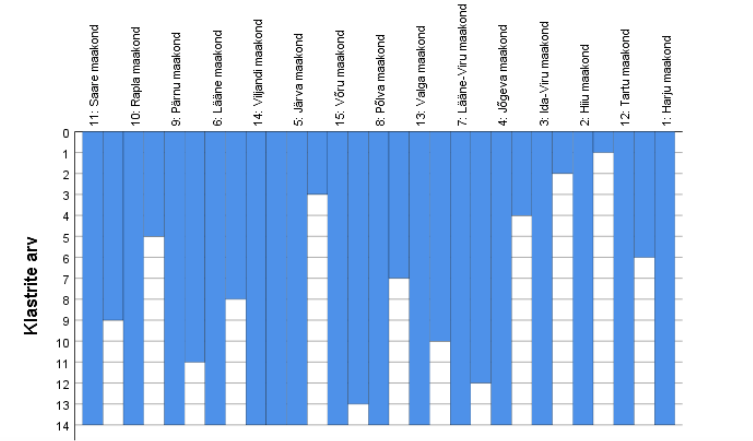
Ühendamistabelis (tabel 5) näidatakse eriti detailselt, kuidas ühendamine toimus (kahjuks kasutatakse siin objektide numbreid, mitte nimesid). Igale ühinemissammule vastab oma rida, st tabelis on ridu ühe võrra vähem kui objekte. Esimesel sammul ühinesid maakonnad 5 ja 14 (Viljandi ja Järva). Järgmine tegevus selle klastriga toimub 7. sammul, mil nende juurde ühineb maakond 6 (Lääne), kusjuures maakonnaga 6 toimus eelmine tegevus 4. sammul (ühinemine Pärnuga). Seega seitsmendal sammul ühinevad maakonnad 6, 9, 5 ja 14. Järgmine tegevus toimub 10. sammul, kus nende juurde ühineb 6. sammul ühinenud paar – 10 ja 11 (Saare ja Rapla). Viimasel sammul ühinevad kõik maakonnad.
Tabelis olev ühendamiskordaja näitab, kui suurel kaugusel ühinemine toimus, kusjuures kaugused kasvavad samm-sammult, sest esmalt ühendatakse võimalikult lähedased klastrid. Suurema hüppe koht ühinemiskordajates näitab kätte, mis sammul ühendamisel tekkis suhteliselt vähemühtne klaster. Selle eel olev seis võiks olla valitud lõppklasterduseks. Suuremale hüppele vastab dendrogrammil pikem horisontaalne joon kahe ühinemissõlme vahel. Joonisel 5 on kujutatud maakondade näite ühendamiskordajad.
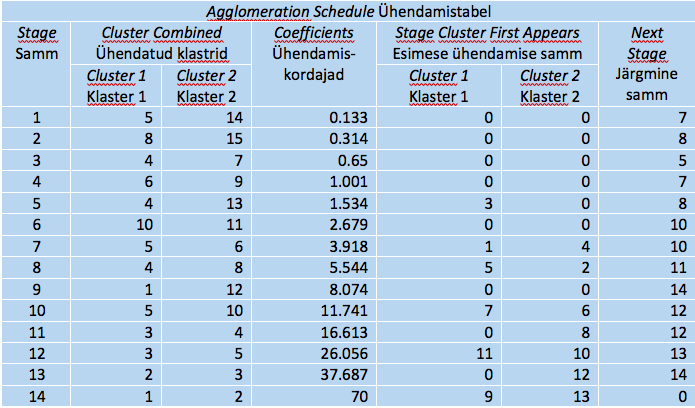
Klasterduse algus kulgeb ühetaoliste vahedega, mida näitab dendrogrammil ühinemissõlmede kuhjumine diagrammi vasakpoolsesse ossa. Suuremad hüpped on näha alates 10. sammust, mis vastabki meie poolt valitud neljaklastrilisele liigitusele.
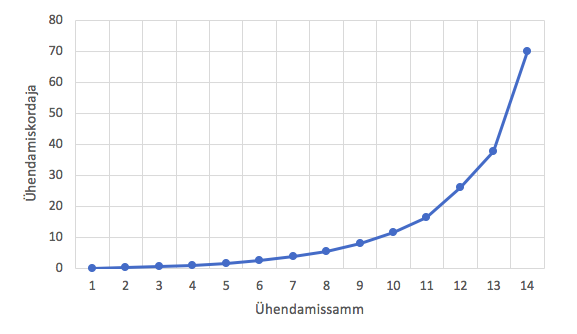
Mida teha klasterdusega edasi? Tekkinud rühmi võiks iseloomustada klasterdustunnuste või ka mõnede teiste tunnuste väärtuste poolest. Tabelis 6 on esile toodud maakondade nelja klastri puhul klasterdustunnuste väärtuste piirid. Näeme, et klastrid eristuvad üksteisest päris selgesti.
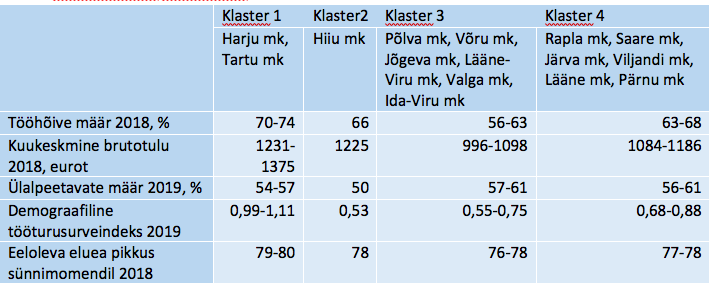
Klastrid 3 ja 4 on sarnased ülalpeetavate määra ja prognoositava eluea poolest, kuid kuu keskmine brutotulu jääb eri vahemikesse, samuti tööhõive määr. Klastri 1 näitajad on “paremad” kui ülejäänud klastreis. Hiiumaa eripära on kõrge kuu keskmine brutotulu suhteliselt kõrge tööhõive määra ja madala ülalpeetavate määra ning madala demograafilise tööturusurveindeksi korral. Hiiu maakonnas elab tööealine ja tööl käiv rahvas, aga noori ei ole peale tulemas või on tööturult peatselt lahkujate hulk suur (maakonna elanike vanuseline struktuur ei välista sellist seletust).
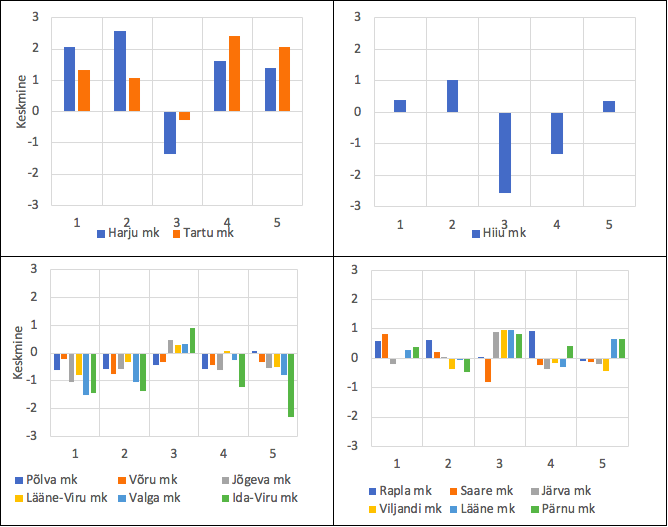
Tunnused: 1–tööhõive indeks 2018, 2–kuukeskmine brutotulu 2019, 3–ülalpeetavate määr 2019, 4–demograafiline tööturusurve indeks 2019, 5–eeloleva eluea pikkus sünnimomendil 2018
Klastrite võrdlus on ilmekam joonise 6 abil, kus on esitatud klasterdustunnuste väärtused klastrite kaupa standarditud kujul (tulp ülespoole tähendab väärtust üle maakondade keskmise ja tulp allapoole – alla maakondade keskmist). Klastrit 3 iseloomustavad allapoole suunatud tulbad, välja arvatud ülalpeetavate määr, mis samuti ei kõnele elujõulisusest. Neljanda klastri maakondades on keskmist ületavaid positiivseid näitajaid, kuid ülalpeetavate määr on keskmiselt veel kõrgem kui kolmandas klastris. Saare maakond sarnaneb muidu Hiiu maakonnaga, aga demograafiline tööturusurve indeks on kõrgem. [/accordion]
k-keskmiste meetod
Mittehierarhilistest meetoditest on laialt levinud ja osutub enamjaolt efektiivseks k-keskmiste meetod. Klasterdus on kiire ka suure objektide arvu korral, sest meetod toetub klastrikeskmistele ega vaja kõigi objektipaaride kaugusi. Tutvustame alljärgnevalt paketi SPSS võimalusi selle meetodi rakendamiseks (standardalgoritm). Siin tekstiosas on objekti asemel suupärasem kõnelda indiviididest, milleks võib olla suvaline uurimisühik (k-keskmiste meetodi sagedane rakendusala on küsitlusandmete analüüs).
Kirjeldame lühidalt klasterduse käiku. Toimub indiviidide iteratiivne (tsükliline) koondamine teatud punktide – klastrite keskpunktide ehk tsentroidide ümber, kuni tsentroidid stabiliseeruvad. Igal iteratsioonisammul tehakse kaks tegevust: indiviidi paigutamine lähima keskpunktiga (tsentroidiga) klastrisse ja seejärel klastri keskpunti ümberarvutus klastri uue koosseisuga. Klastrite arv tuleb ette anda (on miinus selle hea meetodi puhul), kusjuures esimese sammu klastrite keskpunktid kas valitakse vaikimisi (nt teatud võimalikult üksteisest eraldiseisvad indiviidid) või kasutatakse etteantud keskpunkte. Hästi ja põhjendatult valitud klastrikeskmiste etteandmisega saab klasterdust k-keskmise meetodil muuta veelgi efektiivsemaks ja kiiremaks. Suure mahuga andmestiku korral võiks lähtekeskpunktide leidmiseks teha esialgsest andmestikust väiksemal andmestikul (juhuslikul alaosal) eelklasterduse koos klastrikeskmiste salvestusega, mis hiljem on põhilahenduse alguspunkt.
Algoritmi on võimalik varieerida veel sel viisil, et iteratsioonisammu teist osa – klastrikeskmise ümberarvutust – teha indiviidikaupa, iga uue indiviidi lisandumisel (võtmesõna running means). Ohuks kujuneb sel juhul lahenduse võimalik sõltuvus indiviidide järjekorrast. Et seda vältida (selle tõsidust uurida) võiks lahendusi teha ja võrrelda mitme indiviidide juhusliku ümberjärjestuse korral. Ka siis, kui kasutada etteantud klastrikeskmisi, võiks koostada erinevaid klasterdusi keskpunktide erineva järjestusega ning saadud tulemusi ühitada kokkulangevuste poolest.
Klasterdustunnused peavad olema arvulised (või sellistena tõlgendatavad). Kaugusena kasutatakse eukleidilist kaugust, mis tähendab, et eri skaalade ja varieeruvusega tunnused tuleb võrdse mõju saavutamiseks klasterdamisel eelnevalt standardida. Enne klasterdamist võiks uurida erandlike indiviidide olemasolu, et neid klasterdusest välja jätta ja hiljem eraldi käsitleda (selleks vaadelda näiteks klasterdustunnuste jaotusi ühekaupa, seejärel erindi kahtlusega indiviide ka mitme tunnuse poolest korraga).
Klastrite arvu määramine on tõsine otsustuskoht. Lähteks võiksid olla aineteoreetilised kaalutlused või mõni analoogiline juba tehtud töö. Samuti võiks uurida klastrite arvu idee otsimiseks klasterdustunnuste (paarikaupa) hajuvusdiagramme ja panna tähele „tihedamaid“ punktikogumeid. Kui tunnuse jaotusdiagrammil on mitu tipukohta, siis võib olla tegemist mitmeosalise kogumiga – sellised jt esmasanalüüsi võtted võiksid olla abiks. Kindlasti tuleks teha lahendusi mitme klastrite arvuga ja tulemusi individuaalse klastrikuuluvuse alusel uurida, millised klastrid on püsivad klastrite arvu suurendamisel, millised lagunevad kergesti osadeks.
Andmelünkade käsitlus on samuti raske valiku koht, sest klasterdustunnuseid võib olla küllalt suur arv ja kõigi vähemalt ühe andmelüngaga indiviidide kõrvalejätmine võib andmestikku moonutada. Võiks esmalt uurida andmelünkade osatähtsust tunnustes ja kaaluda väga lünklike tunnuste kõrvalejätmist klasterdusest, kui ülesande tähendus sellest ei muutu. Seejärel võiks uurida indiviide klasterdustunnuste poolest ja jätta välja need, kellel on palju klasterdustunnuseid mõõtmata. Nii kujunenud andmestikus (kui see on vähegi kvaliteetne) võiks lünkade arv olla juba selline, et kaugused indiviidide vahel võiks leida paarikaupa valimeid kasutades.
k-keskmiste meetodil saadud klasterduse standardsed osad on järgmised: soovi korral klastrite lähtetsentroidid, iteratsioonisammude tabel, lõplikud klastrite tsentroidid, soovi korral klasterdustunnuste dispersioonanalüüs klastrinumbri suhtes, klastrite suuruste tabel ja soovi korral individuaalse klastrikuuluvuse tabel ning klastritevahelise kauguse maatriks. Soovi korral on võimalik andmestikku salvestada uute tunnustena klastrikuuluvuse tunnus klastrinumbrite kaudu ja individuaalne kaugus klastri keskpunktist. Viimatinimetatu annab võimaluse hinnata klastri homogeensust näiteks klastrisse kuuluvate indiviidide keskmise kauguse kaudu klastri tsentroidi suhtes.
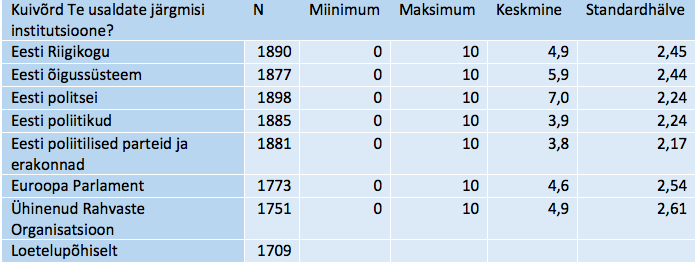
k-keskmiste meetodi rakendus paketis SPSS
Vt ka k-Means Cluster Analysis. IBM Knowledge Center … .
Käsurida Classify – k-means Cluster Analysis toob esile valikud k-keskmiste meetodi korraldamiseks.
Variables – sellele väljale kanda klasterdustunnused.
Label cases by – sellele väljale kanda objektide nimede tunnus, kui selline on olemas; suure indiviidide arvu korral tavaliselt ei kasutata.
Number of clusters – anda ette klastrite arv.
Method – valida Iterate and classify, kui on vaja iteratiivselt leida klastrite tsentroidid ja rühmitada; valida Classify only, kui klastrite tsentroidid on välja Cluster Centers abil ette antud mõne varasema lahenduse või muu allika abil saaduna.
Cluster Centers – võimaldab korraldada klastrikeskpunktide valikuid:
Read initial – kasutada varem salvestatud klastrite tsentroide; selleks kas avada (ajutine, eelmisel lahenduskäigul salvestatud tsentroidide fail, Open dataset ja osutada nimi) või salvestatud tsentroide sisaldav fail (valida fail väljal External data file);
Write final – kirjutada kas eraldi (ajutise) andmestikuna (New dataset koos nime osutamisega) või salvestada püsiva failina (Data file koos nime osutamisega) tsentroide sisaldav andmestik, mida mõnes järgnevas lahenduses kasutada k-keskmiste meetodi lähteks, et lahendust veelgi kiirendada.
Iterate – puudutab arvutusi tsentroidide leidmisel:
Maximum Iterations – suurim tsentroidide nihutuste arv (iteratsioonide arv), siin võiks olla küllalt suur arv, kui andmestik ei ole hiigelsuur ja lahendus võiks kesta väga kaua); kui selle arvu kohane hulk tsükleid on läbi tehtud, siis tsentroidide täpsustamine peatub; kui tsentroidide püsivus saabub varem, siis protsess samuti peatub;
Convergence criterion – teine iteratsiooniprotsessi juhtimise vahend; tsentroide parandatakse seni, kuni need siin antud koondumiskriteeriumi kohaselt enam ei muutu; mida väiksem kriteerium, seda kauem tsentroide viimistletakse;
Use running means – selle nupu sisselülitamisel arvutatakse tsentroidid ümber iga üksiku objekti juurdetoomise järel; kui see nupp ei ole sisse lülitatud, siis tehakse ümberpaigutus konkreetsel iteratsioonil seejärel, kui kõik objektid on mingi tsentroidi juurde paigutatud; selle nupu kasutamisel võib tulemust mõjutada objektide (ja tsentroidide) järjestus.
Save – juhitakse klasterdustulemuste salvestamist:
Cluster membership – andmestiku lõppu lisatakse tunnus, mille individuaalseks väärtuseks on selle klastri number, kuhu indiviid paigutati viimasel klasterdussammul; tunnusel on standardnimi algusega QCL_ .
Distance from cluster Center – andmestiku lõppu lisatakse tunnus, mille individuaalseks väärtuseks on objekti kaugus selle klastri tsentroidis, kuhu see objekt kuulub; tunnusel on standardnimi algusega QCL_ ; otstarbekas on nime muuta sisu kajastavaks.
Options – suvandite abil saab kujundada klasterdustulemust ja korraldada andmelünkade käsitlust:
Statistics – vajadusel saab esile tuua lähteks olnud/valitud klastrite keskpunktid (valida Initial cluster centers);
ANOVA table – soovi korral võib läbi teha klasterdustunnuste dispersioonanalüüsi klastrinumbri suhtes ja tuua esile vastava dispersioonitabeli;
Cluster information for each case – kui indiviide ei ole väga palju, siis võib tuua esile nimestiku, millest näeb iga indiviidi korral, mis klastrisse ta kuulub;
Missing values – saab määrata, kas indiviidid, kelle vastustes on puuduvaid väärtusi, jäetakse analüüsist välja klasterdustunnuste loetelu alusel (Exclude cases listwise) või tehakse arvutused paarisvalimite alusel (Exclude cases pairwise).
Näpunäide klasterdustunnuste standardimiseks: Descriptives – valida Save standardized values as variables; standarditud väärtused salvestatakse andmestiku lõppu standardnimega, mille alguseks on Zscore:.
k-keskmiste meetodi näitena vaatleme Eesti inimeste klasterdust poliitilise usalduse hinnangute alusel, kasutades Euroopa sotsiaaluuringu andmeid 2018. aasta kohta (vt European Social Survey …; andmed on vabakasutuses). Poliitilise usalduse tunnuste plokis on vastused küsimusele „Kuivõrd Te usaldate järgmisi institutsioone?“ Eesti Riigikogu, õigussüsteemi, politsei, poliitikute, poliitiliste parteide ja erakondade kohta ning Euroopa Parlamendi ja Ühinenud Rahvaste Organisatsiooni kohta. Vastati skaalal, kus 0 tähendab „ei usalda üldse“ kuni 10, mis tähendab „usaldan täielikult“. Tabelis 7 on näidatud vastuste arvud ja esmased statistikud. Tunnused on erisuguse variatiivsusega skaalal 0 kuni 10 (keskmised 4 kuni 7, standardhälbed 2,2 kuni 2,6), mis tähendab kindlat standardimise vajadust.
Uurisime ka klasterduseks valitud tunnuste vahelisi korrelatsioonikordajaid, mis osutusid olevat valdavalt mõõdukal tasemel. Siiski poliitikute ja poliitiliste parteide usaldushinnangute vaheline seos on kordajaga 0,84 (vastastikuse kirjelduse määr 71%, mis läheneb dubleerimisele), mistõttu jätsime välja poliitikute usaldushinnangu, et seda sisulist aspekti mitte üle tähtsustada. Ülejäänud tunnuste vahelised korrelatsioonikordajad on vahemikus 0,37–0,76. Tehniliselt ei ole k-keskmiste meetodi puhul klasterdustunnuste seos keelatud, aga siin võiks mõelda pigem sisule. Mis tähendusega tunnused klasterdustunnusteks võtame, sellise tähendusega saame ka klastrid.
Nagu näha tabelist 7, koosneks loetelupõhine täisvastustega andmestik 1709 indiviidi andmeist. Siiski läksime siin teist teed (võib-olla mitte kõige õigemat) ja kasutasime kauguste arvutamisel paarisvalimeid. Julgust andis hinnangute ploki lünklikkuse analüüs, millest selgus, et on üks indiviid, kes ei ole ühelegi küsimusele vastanud (jääb muidugi välja), aga alla pooleteise protsendi on neid, kes on vastanud mitte rohkem kui kolmele küsimusele kuuest. Kõigile küsimustele vastas 90% ja neljale või viiele kuuest – 9%.
Tutvustame neljaklastrilist klasterdust. Koostasime ka kolmeklastrilise, mis osutus suhteliselt ettearvatuks: tekkisid (kokkuleppeliselt nimetades) madala, keskmise ja kõrge poliitilise usaldusega isikute rühmad (vastavalt 431, 842 ja 630 indiviidi), milles oli siiski ka huvitavaid momente. Näiteks keskmise usalduse rühmas on poliitiliste parteide usaldus keskmiselt madalam kui üldiselt, mille tõttu on kõrge poliitilise usalduse rühmas usaldus parteide ja erakondade vastu eriliselt kõrge (keskmise tasakaalustamiseks). Neljaklastrilise liigituse tulemused esitatakse sama ülesehitusega tabelitena, nagu paketi SPSS väljundtulemustes, et saaks näidet kaasa lahendada. Artiklis või muus kirjutises esitamiseks on kindlasti otstarbekas tabeleid koondada.
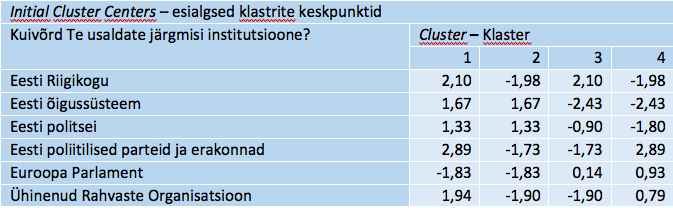
Rakendatud iteratsiooniprotsessi lähteks olid näite korral tabelis 8 esitatud keskpunktid iga klasterdustunnuse ja klastri kohta – neli võimalikult erinevat indiviidi. Selle tabeli vastu võiks olla huvi nägemaks, kui palju klastri keskpunktid lõppseisuni on muutunud, sisulist infot siin ei ole. Kui anname lahenduseks tsentroidid ise ette, siis muidugi on sel tabelil tähtsus identifitseerimaks konkreetset klasterdust.
Iteratsiooniprotsess indiviidide ümberpaigutamise ja klastrikeskmiste ümberarvutusega võib lõppeda kahel viisil: saab täis etteantud arv tsükleid või klastrite tsentrid enam ei muutu teatud läve kohaselt. Tabelist 9 on näha, et seekord kulus 21 ümberpaigutust, enne kui keskpunktid stabiliseerusid (praegu oli läveks väga väike arv ja väga suur lubatav iteratsioonide arv). Iteratsioonide arvu on mõtet tõkestada väga suuremahuliste andmestike korral, et lahendusaega piirata, muidu võiks siin piirarv olla suur, et protsess läheks klastrikeskmiste stabiliseerumise lõpuni. See tabel on informatiivne lahenduse tehnilise külje huvilistele.
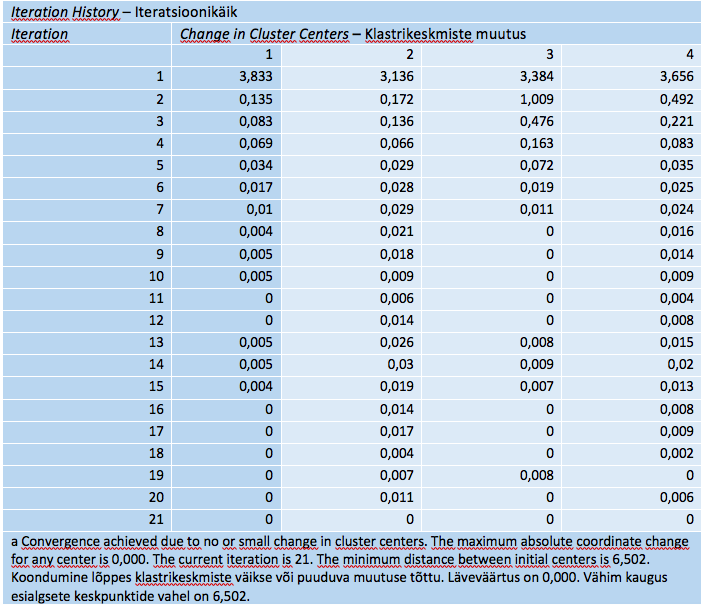
Järgneb klasterdustulemust sisuliselt peegeldav tabel lõplike klastrite keskpunktidega (tabel 10). Nende kaudu saame anda klastritele tähenduse ning võimaluse ja vajaduse korral suure ettevaatusega ka nime. Ettevaatust on vaja selleks, et nimes kajastuks klastri sisu võimalikult täpselt, mis ei ole uurijale lihtne valik.
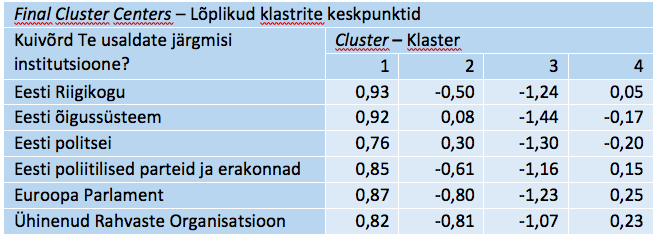
Klastrisse 1 kuuluvad indiviidid, kellel on kõik poliitilise usalduse hinnangud keskmiselt üle üldise taseme, milleks on standarditud andmetel 0 (vt ka joonist 7 klastrite keskpunktide kohta). Hälve üldisest tasemest ülespoole on olenevalt tunnusest 0,8–0,9 võrra. Klastrile 1 moodustab tugeva kontrasti klaster 3, kus kõik usaldushinnangud on tugevalt alla üldise taseme (1,1 kuni 1,4 võrra). Klastrid 2 ja 4 omavahel moodustavad samuti teatava kontrasti. Klastri 2 indiviidid annavad suhteliselt madala hinnangu Riigikogule, parteidele ja kahele välisinstitutsioonile, kuid on keskmisel tasemel või üle selle õigussüsteemi ja politsei usalduse poolest. Klaster 4 koosneb üldiselt „keskmiste“ vaadetega indiviididest: õigussüsteemi ja politsei usaldus keskmise lähedal natuke alla selle, kuid ülejäänud institutsioonide usaldus keskmise lähedal, natuke üle selle. Need on usaldushinnangute nö tüübid Eestis aastal 2018 (kui otsida nelja usaldusrühma – klastrite arv on meie valik).
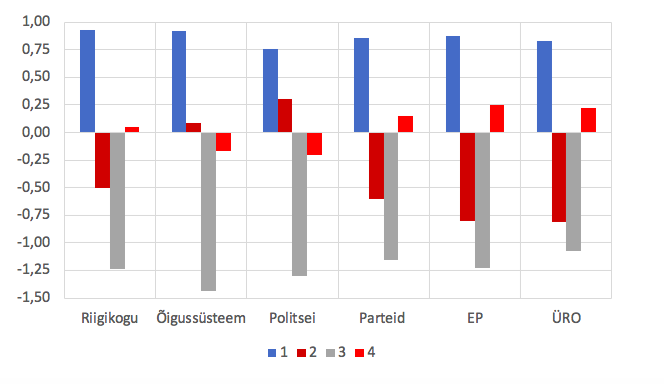
Soovi korral võib järele uurida, kuivõrd suurt rolli ja kas ühetaolist mängivad klastrite eristamisel valitud klasterdustunnused. Selleks tuuakse esile dispersioonanalüüsi tabel (koos ettevaatusele kutsuva märkusega olulisuse tõenäosuse kasutamisel, tabel 11). Siin võiks F-suhteid tähele panna.
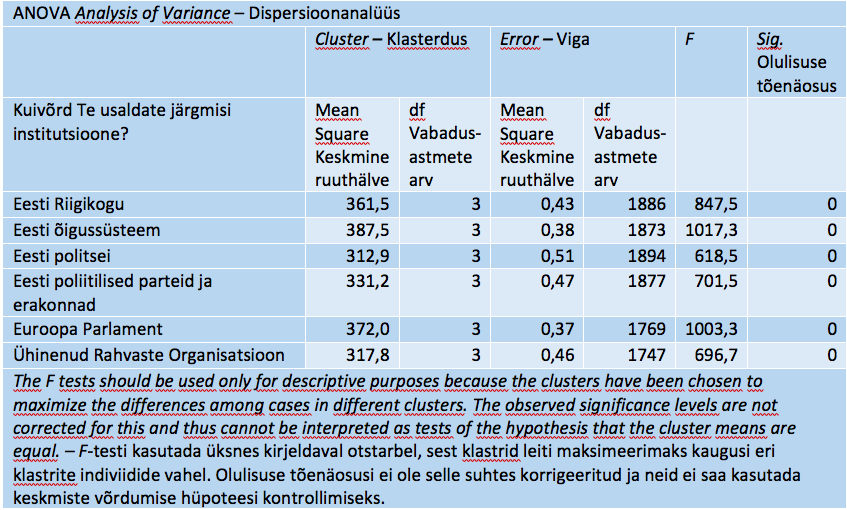
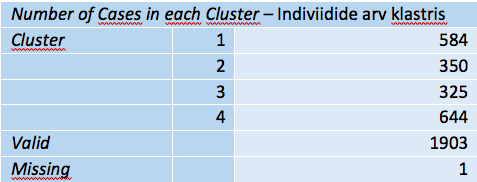
Tabelis 12 näidatakse klastrite suurused samas järjekorras nagu eespool. Ühtlaselt suure usaldusega klastris on 584 indiviidi (31%) ja vähese usalduse klastris 325 indiviidid (17%). Vähese usalduse rühmas, politsei ja õigussüsteem välja arvatud, on 350 indiviidi (18%) ja keskelt läbi keskmise usaldusega, väikeste kõikumistega siia-sinna, on rühm, mis koosneb 644 indiviidist (34%). Rühmitus on suuruse poolest vastuvõetav: mitte ükski rühm ei ole väga väike, suurima-vähima suhe on 2 ringis.
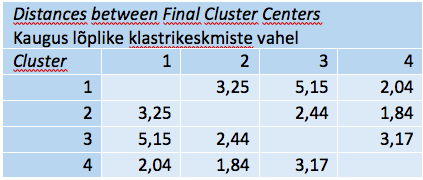
Klastritevaheliste kauguste maatriksist (tabel 13) näeme juba tuttavat pilti: teineteisest suhteliselt kaugel on klastrid 1 ja 3 (kaugus 5,2). Klastrid 2 ja 4 on teineteisele suhteliselt kõige lähemal (kaugus 1,8), mis klastrikeskmiste vaatlemisel tabelis 10 ja joonisel 7 väga välja ei paistnudki. Klastritevahelise kauguse tabel täiendas meie ettekujutust klastreist. Täpsustame seda veelgi, kasutades muid andmestikus olevaid tunnuseid peale klasterdustunnuste.
Tabelis 14 on esitatud mõned täiendavad keskmised andmed moodustatud klastrite kohta tunnuste abil, mis ei olnud klasterduse aluseks. See annab võimaluse klastreid täiendavalt iseloomustada ja nende tähendust täpsustada lisaks klasterdustunnuste kaudu arvutatud tsentroididele. Esimese, suure usalduse klastri liikmed on teistest keskmiselt nooremad, pikema kooliajaga, enam rahul niihästi eluga üldiselt kui ka majanduse olukorraga Eestis. Nad pooldavad Euroopa jätkuvat ühinemist. Teist klastrit eristab neljandast kõrgem vanus ja veidi lühem kooliaeg, madalam rahulolu ja eitav suhtumine Euroopa ühinemisse. Kolmandasse klastrisse kuuluvad indiviidid on suhteliselt lühema kooliajaga, kõige vähem rahulolevad ja Euroopa jätkuva ühinemise vastu. See näide rõhutab klastrite tähenduse avamise vajadust ka indiviidide tausta poolest, mis klastrinumbrite tunnuse loomise kaudu on tehniliselt lihtsalt tehtav.
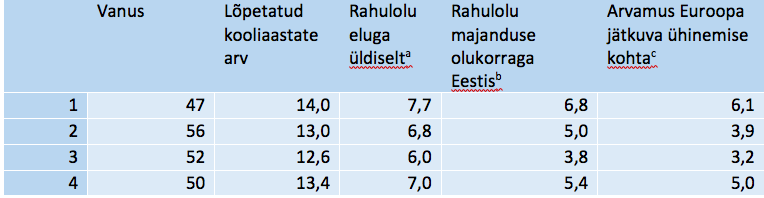
aKõike kokkuvõttes, kuivõrd rahul Te oma eluga üldiselt olete praegu? bKuivõrd rahul olete üldiselt Eesti praeguse majandusliku olukorraga? 0-ei ole üldse rahul, 10-olete väga rahul. cMõeldes Euroopa Liidule ütlevad mõned, et Euroopa ühinemine peaks jätkuma. Teised aga arvavad, et see on läinud juba liiga kaugele. Milline number skaalal kirjeldab kõige paremini Teie arvamust? 0-ühinemine on läinud juba liiga kaugele, 10-ühinemine peaks jätkuma
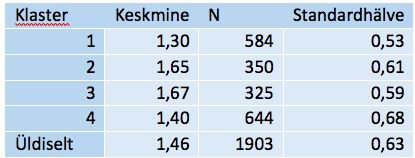
Kui ühtsed on moodustatud klastrid? Sellele saame vastuse, kui arvutame klasteranalüüsi käigus ka iga indiviidi kauguse selle klastri tsentrist, kuhu indiviid lõpuks paigutati. Tabelist 15 näeme, et meie näites on kõige kompaktsem (klasterdustunnuste alusel) esimene, suure usalduse klaster (keskmine kaugus klastri keskmest 1,3 teistest väiksema standardhälbega 0,53). Suhteliselt ”hõredamalt” paiknevad kolmanda ja teise klastri indiviidid: keskmine kaugus tsentrist üle 1,65–1,67, seega suurem kui üldkeskmine kaugus 1,46.
Individuaalseid klastrinumbreid selles näites tabelina esile ei toodud, kuid see oleks võimalik ja võiks huvi pakkuda mõne väiksema andmestiku puhul. Võimalus lisada klastrinumbrid andmestikku nende edasiseks kasutamiseks on klasterdusprogrammides tavaliselt olemas.
Kahesammuline klasteranalüüs
Kahesammuline klasterdus (ik TwoStep Cluster Analysis), mis on realiseeritud paketis SPSS, on kiire ja sobib ka suurte andmekogumite klasterdamiseks, kusjuures üheaegselt on võimalik kasutada nii kategoriaalseid kui ka pidevaid tunnuseid.
Esimene samm on eelklasterdamine (ik pre-clustering), kus vaadatakse läbi kõik indiviidid ja paigutatakse iga indiviid kauguse alusel kas mõnesse olemasolevasse eelklastrisse või luuakse vajadusel uus. Saadud eelklastrite andmestik on lähteks teisele sammule, kusjuures eelklastri liikmeid käsitletakse ühtmoodi, koos, ühe objektina. See tähendab teise sammu lähteks andmestikku, mille objektide arv on esialgsest indiviidide arvust märgatavalt väiksem, nimelt eelklastrite arv, ja see tagabki algoritmi suure kiiruse. Teine samm on eelklastrite hierarhiline klasterdamine.
Algoritm toetub klasterdamisel tõepärafunktsiooni kasutavatele informatsioonikriteeriumidele AIC (Akaike kriteerium) ja BIC (Bayesi informatsioonikriteerium). Soovitav on kasutada mõlemat teineteise järel ja pakutud lahendused ka tõlgenduslikult ja rakenduslikult läbi mõelda. Mõlemad kriteeriumid töötavad põhimõttel „vähem on parem“. Üht klasterdust samas ülesandes võib pidada paremaks ja paremini sobitunuks andmetega kui teist (nt teise klastrite arvu korral), kui selle informatsioonikriteerium on väiksem kui teisel. Kordajatel AIC ja BIC ei ole normväärtusi ega ülemtõket ja neid käsitletakse võrdlevalt.
Kaugusena on võimalik kasutada tõepärafunktsioonil põhinevat kaugust ja pidevate tunnuste puhul ka eukleidilist kaugust. Kahe klastri vaheline kaugus logaritmilise tõepärafunktsiooni kaudu defineeritakse selle alusel, kui palju kasvab tõepärafunktsioon, kui klastrid liita üheks (lühike sissevaade matemaatilisse külge nt Bacher jt 2004). Eeldatakse indiviidide sõltumatust üksteisest, pidevate tunnuste normaaljaotuse kohast jaotumist ja üksteisest sõltumatust. Kategoriaalsete tunnuste puhul eeldatakse jaotumist klastreis multinomiaalse jaotuse kohaselt. Need on päris ranged piirangud ja selliseid lähteandmeid on klasteranalüüsi jaoks raske leida (sh mittekorreleeritus). Siiski märgitakse ka mooduli tehnilistes saatematerjalides, et meetod on küllaltki tundetu nende eelduste rikkumise suhtes (vt TwoStep Cluster Analysis. IBM Knowledge Center …).
Praktika on näidanud, et kahesammulise protseduuri eristusvõime on hea, kui klasterdustunnused on pidevad, kuid kategoriaalseid tunnuseid kaasates kaldutakse klasterdamisel neid üle tähtsustama ja vahel määratakse klastrid eelkõige kategoriaalsete tunnuste järgi. Algoritm määrab soovi korral ise klastrite arvu, valides liigitust optimeeriva hulga klastreid. Pakutud klastrite arvu tuleb suhtuda kriitiliselt ja arvestada selle heakskiitmisel konkreetse uurimisülesande vajadustega.
Kahesammulise klasteranalüüsi üheks plussiks on tulemuste lihtne loetavus. Arvutabelite kujul väljundiga harjunud uurijale võib selle mooduli visualiseeritud tulemuste esitus tunduda ehk pisut liiga „ligikaudsena“, aga klasteranalüüsi vältimatut subjektiivset komponenti arvestades on üldmulje loomine vahel olulisemgi kui arvude näiline väärikus.
Kahesammuline klasteranalüüs paketi SPSS abil
Lihtrakendus
Vt ka TwoStep Cluster Analysis. IBM Knowledge Center … .
Käsurida Analyze – Classify – Two-Step Cluster Analysis avab akna kahesammulise klasteranalüüsi põhivalikute tegemiseks.
Categorical Variables – sellele väljale kanda kategoriaalsed klasterdustunnused.
Continuous Variables – sellele väljale kanda pidevad (pidevana tõlgendatavad) klasterdustunnused.
Distance Measure – kauguse valik kas tõepärafunktsiooni kaudu (Log-likelihood) või eukleidiline kaugus (Euclidean); eukleidilist kaugust saab valida siis, kui ei kasutata kategoriaalseid tunnuseid; tõepärafunktsiooni põhine kaugus väljendab klasterduse tõepärafunktsiooni muutust, kui konkreetne objekt paigutada teatud klastrisse; eeldatakse tunnuste sõltumatust ja jaotust normaaljaotuse kohaselt.
Number of clusters – klastrite arvu saab lasta leida automaatselt (Determine Automatically) piirates klastrite arvu maksimumi etteandmisega või nimetada ise (Specify fixed).
Count of Continuous Variables – klasterdustunnuseid on tungivalt soovitav standardida ja siin näidatakse, kui mitu neist tuleb standardida lahenduse käigus ja kui mitu on juba eelnevalt standarditud.
Clustering criterion – klastrite arvu ja klastrite määramiseks iseloomustatakse klasterstruktuuri sobitust andmetega tõepärafunktsiooni kaudu kasutades kas Schwarzi (Bayesi) kriteeriumi BIC või Akaike kriteeriumi AIC (traditsioonilised suurused tänapäevase regressioonanalüüsi juures; “karistavad” suure indiviidide arvu ja suure tunnuste arvu eest mitmemõõtmelise mudeli koostamisel); ei teeks paha lahendada järjest mõlema kriteeriumiga; toimivad põhimõttel “väiksem on parem”.
Options – suvandite kaudu saab reguleerida lahendust enamjaolt selliste parameetritega, mis nõuavad aluseks oleva algoritmi detailsemat tundmist kui siinkohal jutuks (avage silmitsemiseks nupp Advanced – kehtestatakse analüüsi aluseks oleva liigituspuu konstruktsiooni piirangud, sh eelklastrite arv; jääb vaikimisi).
Outlier treatment – nupp Use noise handling korraldab erindite käsitlust; ligilähedaselt selles mõttes, kas jätta erindid kõrvale (kood -1) või püüda neid mahutada liigituspuusse; erindite olemasolu võiks võimaluse korral uurida juba enne klasteranalüüsi.
Standardization of continuous variables – näidatakse tabelit, kus saab määrata standardimist vajavad tunnused, suunates need väljale To be standardized; vaikimisi standarditakse kõik pideval skaalal mõõdetud tunnused.
Output – kujundatakse klasterdustulemused:
Pivot tables – toob esile klastrikeskmiste tabeli;
Charts and Tables in model Viewer – valiku Evaluation Fields abil saab määrata tunnused, mille abil iseloomustada klastreid täiendavalt (mitte klasterdustunnused);
Create cluster membership variable – seda valides salvestatakse klastrinumbrite tunnus standardnimega, mille algus on TSC_;
XML Files – klasterduse lõpptulemused saab salvestada etteantud nimega failidena.
Kahesammulise klasteranalüüsi näite toome Euroopa sotsiaaluuringu 2018. aasta andmeil Eesti kohta (European Social Survey …). Seame ülesandeks leida klastrid arvamuste alusel immigratsiooni mõju kohta Eestile, kaasates vanuserühma (nooremad kui 35; 35 aastat kuni 64; 65 aastat ja enam) ja kolm hinnangut vastavalt majanduses, kultuurielus ja üldiselt elus avalduva immigratsiooni efekti kohta. Nagu arvata, ei ole siin tegemist rangelt sõltumatute tunnustega, sest hinnang ühe elukülje puhul korreleerub hinnanguga teise elukülje puhul: korrelatsioonikordaja 0,6–0,7 ringis.
Mida sellisel juhul teha, et meetodi eeldusi rahuldada, aga info säilitada? Üks võimalus on rakendada tunnuste teisendust peakomponentideks, mis teatavasti on mittekorreleeritud ja annavad summaarselt edasi 100% esialgsest variatiivsusest, kui moodustada tunnuste arvuga võrdne arv peakomponente. Meie ülesandes osutusid peakomponendid ligikaudu kolme algtunnuse omapärakomponentideks (igaühel üks suur laadung ja ülejäänud väiksed, aga mitte nullid). Siiski me ei lähe seda teed ja eeskätt nö didaktilistel kaalutlustel, sest peakomponentide väärtusi (standarditud, kuid siiski subjektiivse tõlgendusega) oleks tulemuste seletamisel keeruline kasutada. Lähme eelduste osalise eiramise teed ja loodame lahendi stabiilsusele eelduste nõrga arvestamise juhul.
Kolm pidevat tunnust, mida lisaks vanuserühmale (kategoriaalne tunnus) kasutame, on järgmised (hinnangu andnute arvud vastavalt 1860, 1874, 1867).
- Üldiselt hinnates, kas see mõjub Eesti majandusele hästi või halvasti, kui teistest riikidest inimesed siia elama tulevad? 0 – mõjub majandusele halvasti, 10 – mõjub majandusele hästi; keskmine 4,8, standardhälve 2,4;
- Mida Te arvate, kas teistest riikidest inimeste Eestisse elama asumine pigem kahjustab või rikastab Eesti kultuurielu? 0 – kahjustab kultuurielu, 10 – rikastab kultuurielu; keskmine 5,1, standardhälve 2,4;
- Kas Eesti muutuks elukoha mõttes halvemaks või paremaks paigaks, kui teistest riikidest inimesed siia elama tulevad? 0 – halvemaks elupaigaks, 10 – paremaks elupaigaks; keskmine 4,4, standardhälve 2,1.
Saadud klasterduse toome esile võimalikult nende tabelite-jooniste kaudu, mis kuuluvad paketi SPSS väljundisse selle mooduli korral. Artiklis või muus publitseeritavas töös vajavad need kindlasti kohendamist.
Joonisel 8 on esitatud saadud klasterduse üldvaade. Algoritm pakub (mõlema kriteeriumi, nii AIC kui BIC korral) seitsmeklastrilist lahendust. Lisaks illustreeritakse graafiliselt klasterduse kvaliteedi iseloomustamiseks siluetikordaja (ik silhouette measure) väärtust.
Siluetikordaja tähenduse määravad kaks keskmist kaugust: elemendi kaugus oma klastri tsentrini ja kaugus lähima mitte-oma klastri tsentrini. Parimal klasterdusel on kõigi indiviidide peale kokku esimene kaugus nullilähedane ja halvimal juhul on nullilähedane teine nimetatud kaugustest. Nende kauguste kaudu määratud vahe teatud standarditud viisil määrabki siluetikordaja piirides -1 kuni 1. Selles vahemikus on SPSS määranud (kokkuleppeliselt muidugi) halva, keskmise ja hea lahenduse tsoonid, mida näidatakse värvidega. Negatiivne skaalaosa tähendab seda, et oma klastri sees on kaugused suuremad kui klastrite vahel (väga ebaloomulik tulemus). Positiivne skaalaosa tähendab vastupidist ja soovitavat olukorda: oma klastri sees on kaugused väiksemad kui klastrite vahel.
Et siluetikordaja on meie näites seitsmeklastrilises lahenduses rohelise ala piiril (silma järgi 0,45, vasakpoolne diagramm), siis võiksime klasterdust usaldada. Siiski proovime, millise tulemuse saaksime väiksema, etteantud klastrite arvu, nt nelja klastri korral. Nagu samalt jooniselt nähtub, ei vähenenud kvaliteet märgatavalt (ikka hea klasterduse poolel, parempoolne diagramm), aga klastrid on loodetavasti suuremad ja niiviisi tulemus statistiliselt suurema kaaluga klastri edaspidise analüüsi seisukohalt. Joonisel kujutatu on ”uks” klasterduse lähivaate aknasse (ik Model Viewer) ja see avaneb topeltklõpsuga.
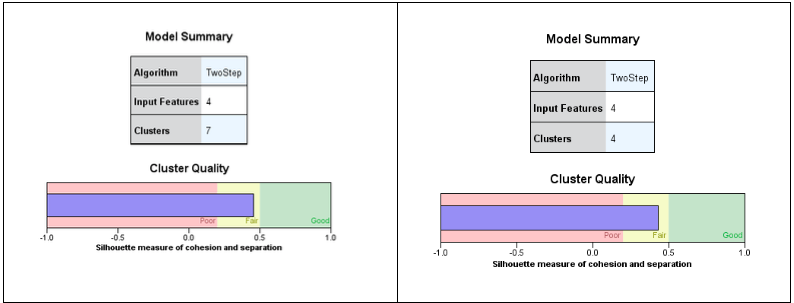
Mudeli lähivaate aknal on kaks poolt: vasak pool klastrite kokkuvõtteks ning parem pool üldandmeiks ja vasaku poole üksikelementide suumitud uurimiseks. Kui avada neljaklastriline klasterdus mudeli aknas, siis näeme vasakus aknapooles joonisel 8 (parempoolne diagramm) ja paremas aknapooles joonisel 9 esitatud pilti.
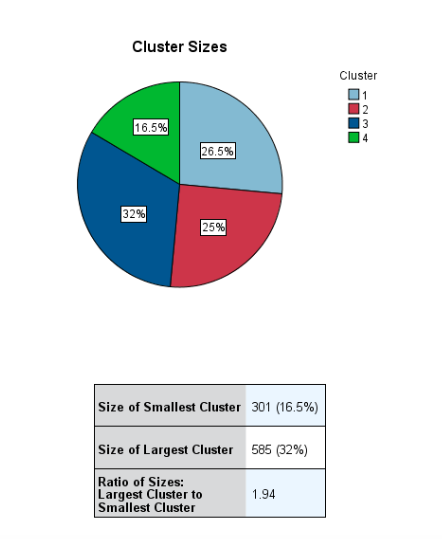
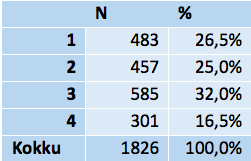
Nagu näha jooniselt 9, on kogumi jaotus neljaks klastriks nende suuruse poolest vastuvõetav. Ükski klaster ei ole väga väike ja vähim klaster on suuruse poolest pisut enam kui pool suurimast. Tabelist 16 näeme, et klasterdamises osales 1826 indiviidi. Et kokku küsitleti 1904 indiviidi, siis läks lünkade tõttu kaotsi 78 (4%), mis ei ole palju vastamisel nii keerulisele küsimusele, nagu on seda immigratsiooni mõju.
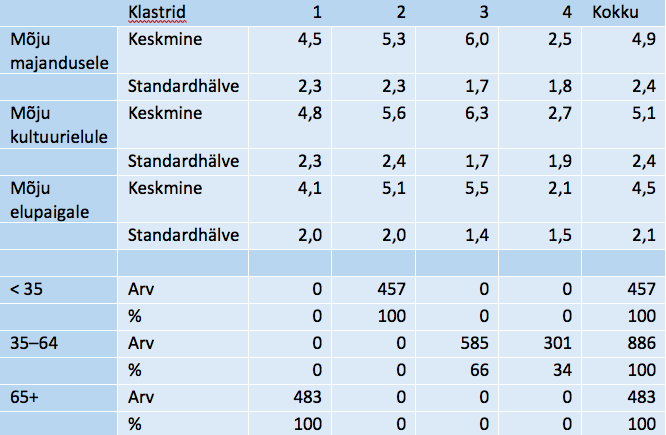
Klastrite profiil klastrite keskpunktide ja vanuserühmade vahelise jaotuse järgi on kokkuvõtlikult esitatud tabelis 17. Kommentaari selle jaotuse kohta toome analoogilise teabe kohta tehtud joonise 10 juures.
Pöördume tagasi lähivaate akna, st graafilise tulemuste esituse juurde.
Vasakpoolse akna vaated
Mudeli akna kummalgi poolel on mitu vaadet. Vasakul poolel näeme mudeli kokkuvõtet (ik Model Summary) ja veel on selles aknapooles võimalik asuda klastrite vaate juurde (ik Clusters View). Nende vahel saab akna seisu vahetada akna allservas oleva nupu View abil.
Joonisel 10 on esitatud klastrite vaade – skeem, kus antakse klastrite iseloomustus suuruse (rohekad tulbad rõhtsel tulpdiagrammil), iga klastri vanuseline iseloomustus ja vaadeldava kolme hinnangu keskmised. Veerg skeemil vastab klastrile ja rida tunnusele. Tunnused on järjestatud selle järgi, kui tähtis on tunnus klastrite eristajana. Vanuserühm on praegu suurima tähtsusega klasterdaja (tumedaim toon). Nagu näha, neljaklastrilises liigenduses noorim ja vanim vanuserühm edasi ei jaotu, küll aga keskmine, milles eristuvad immigratsiooni mõjule positiivsete (suuremad keskmised) ja negatiivsete (väikesed keskmised) hinnangute andjad. Kui oleksime avanud ka automaatselt pakutud seitsmeklastrilise liigituse, siis oleksime klasterdusena näinud kõigi vanuserühmade jaotumist osadeks vastavalt positiivsetele ja negatiivsele arvamusele immigratsiooni kohta, keskmine vanuserühm koguni kolmeks. Paraku oleksid siis osa rühmi väikesed ja üldistuseks vähese statistilise kindlusega.
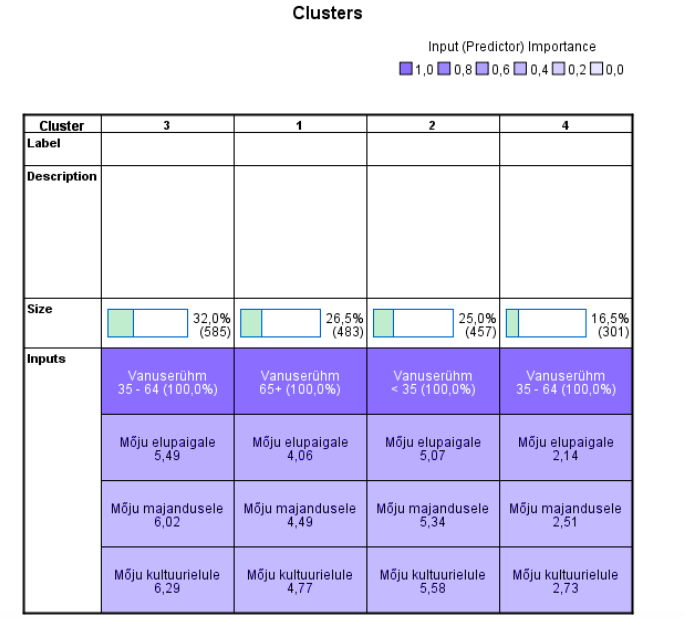
Klastrite vaadet kujundatakse nupureaga Display akna allservas, kusjuures kursori peatumisel nupu juures näidatakse selle nime. Samal moel näeb skeemi lahtreil liikudes sellele lahtrile vastavat lisateavet: kursori peatamisel lahtri kohal näidatakse lahtrit iseloomustavaid arve eraldi hüpikaknas. Nupu Cells show cluster centers abil näidatakse iga klastri korral iga tunnuse keskmist (või kategoriaalse tunnuse puhul protsentuaalset osatähtsust, mis on ühtlasi vaikimisi valik). Samuti osutatakse graafiliselt ja numbriliselt iga klastri suurus.
Tunnuseid saab järjestada tabelis soovitud järjekorras (ja legendi alusel vastavas värvitoonis). Selleks on akna allservas sortimisele viitavad ikoonid ja igaühe juures nimetus: üldise tähtsuse järgi (ik Sort features by overall importance), tähtsuse järgi klastri sees (ik Sort features by importance within cluster), nime järgi (ik Sort features by name) või järjekorra järgi andmestikus (ik Sort features by data order). Nupule vajutamisel vastav tegevus käivitub kohe.
Klastritele võib tabelis anda nimed ja kirjutada juurde vajadusel pikema kirjelduse. Ka klastreid võib ümber sortida nime ja suuruse järgi (ik vastavalt Sort clusters by name/label, Sort clusters by Size). Selleks sobiv nupp on samuti akna allservas.
Peale numbrilise vaate võib esile tuua ka ainult tunnusenimed soovi kohases järjestuses (parempoolseim nupp Cells show basic information). Teisalt saab nuppudega Cells show absolute distribution ja Cells show relative distribution igas lahtris esile tuua vastavalt tunnuse sagedusjaotuse ja protsentjaotuse pinddiagrammide kujul. Sagedusjaotused peegeldavad ka klastrite suurust ja protsentjaotused annavad võimaluse võrrelda klastreid iseloomu poolest. Joonisel 11 on näidatud neljaklastriline liigitus klastrisiseste protsentjaotuste kaudu.
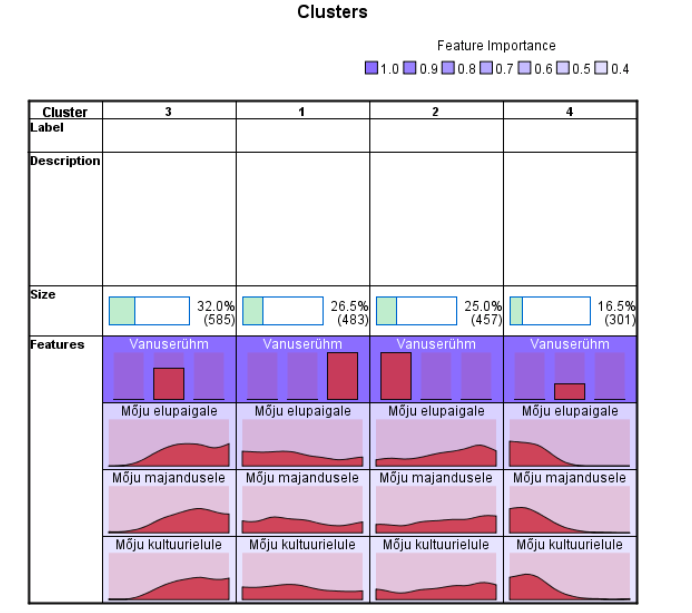
Klastrid on järjestatud suuruse järjekorras. Näeme, et suurimas, kolmandas klastris on kõigi kolme tunnuse jaotused kaldunud positiivse hinnangu poole, kuid neljandas klastris, vastupidi, madalate hinnangute poole. Need mõlemad klastrid koosnevad 35–64-aastastest isikutest. Noorimas vanuserühmas (kuulub tervikuna klastrisse 2) on hinnangud pigem head (aga leidub ka madalaid hinnanguid, vasak serv lahtri jaotuse skeemil) ja vanimas vanuserühmas (kuulub tervikuna klastrisse 1) pigem halvad, aga leidub ka mõju kõrgelt hindavaid isikuid (parem serv lahtri jaotuse skeemil).
Kogu klastrite vaadet saab pöörata: read veergudeks ja vastupidi (vasakpoolseim ikoon aknas, Transpose clusters and Features). See on kasulik vaate parandamiseks (ridu mahub aknasse rohkem kui veerge). Kui tahame mis tahes vaate tühistada, siis aitab nupp Reset algseisu taastada (vahel ka siis, kui aken sattub vaadete vahetusega segadusse. Akna vaadete eri kihte saab hõlpsasti kopeerida akna ülaosas olevate nuppude varal ja eksportida vajalikku kohta.
Parempoolse akna vaated
Mudeli lähivaate akna paremal poolel on neli vaadet nupu View valikuga: jaotus klastreiks Cluster Sizes, vasakus aknapooles märgitud lahtri jaotus valikuga Cell Distribution, tunnuste tähtsuse diagramm klasterdamisel valikuga Variable Importance ja klastrite võrdluse karpdiagramm valikuga Cluster Comparison.
Jaotust klastreiks kujutavat ringdiagrammi vaatlesime juba eespool (joonis 9).
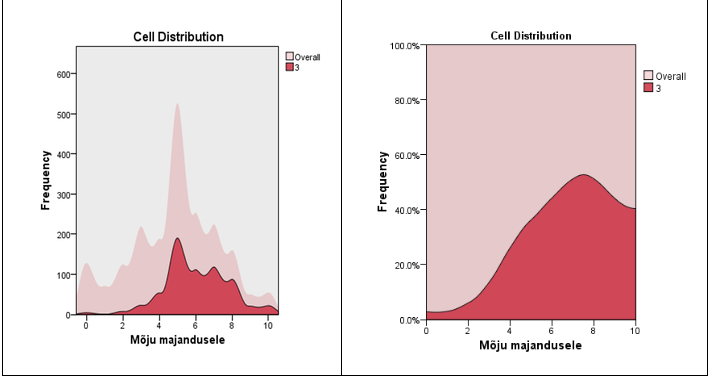
Joonisel 12 on toodud esile suurima rühma (klaster 3, vanus 35–64 aastat) majanduselule avalduva mõju hinnangute lähivaade: sagedusjaotus (vasakul) ja protsentjaotus (paremal). Sagedusjaotuse puhul on osutatud taustaks ka veel üldine jaotus (ik overall). Suumitult näeme üksikasjalikumalt, kuidas on jaotunud vastused klastris, nt protsentjaotuse tipp 7 ja 8 punkti vahel. Jaotuste üksikasjalik vaatlus aitab klastreid paremini tõlgendada. Sellise vaate saamiseks tuleb vastav lahter vasakus aknapoolses aktiviseerida.
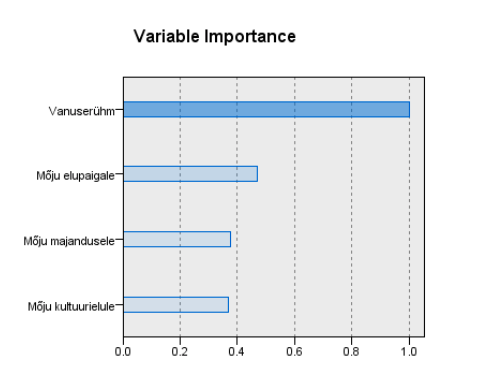
Joonisel 13 on graafiliselt iseloomustatud klasterdustunnuste tähtsust klastrite üksteisest eristamisel (ik Variable Importance). Tunnuse tähtsus klastrite eristajana peegeldab suhteliselt tunnuse osa klasterstruktuuri tekkimisel. Kategoriaalse tunnuse korral on aluseks tunnuse jaotuse võrdlus klastris selle tunnuse üldjaotusega, pideva tunnuse puhul – klastrikeskmise ja üldkeskmise teatav kõrvutus.
Olulisim klasterdustunnus on vanuserühm, nagu juba ka eespool veendusime (joonisel võetud võrdseks arvuga 1). Hinnangutunnused on suhtelisel skaalal enam kui poole väiksema tähtsusega (eespool mainitud kategoriaalsete tunnuste „ülemvõim“ klasterdamisel), neist tähtsaim on mõjuhinnang elupaigale. Selle diagrammi alusel võib mõnikord kaaluda väga väikese tähtsusega tunnuste kõrvalejätmist klasterdusest. Praegu selleks alust ei ole.
Klastrite omavaheline visuaalne võrdlus toimub karpdiagrammi abil. Klastrite võrdlemiseks tuleb vasakpoolses aknas märkida võrreldavate klastrite veerud (kas kõik või erihuvi pakkuvad klastrid). Parempoolses aknas osutatakse valiku View – Cluster Comparison korral iga tunnuse jaoks üldine karpdiagramm (rõhtne ristkülik) ja igas võrreldavas klastris mediaan (marker) ning kvartiilhaare (rõhtsad markerist lähtuvad jooned kvartiilide kauguseni). See on hea ülevaade tunnuse jaotusest nii üldiselt kui ka klastreis. Mida enam erinevad klastrid konkreetse tunnuse poolest, seda tähtsamaks osutus ka see tunnus klastrite koostamisel.
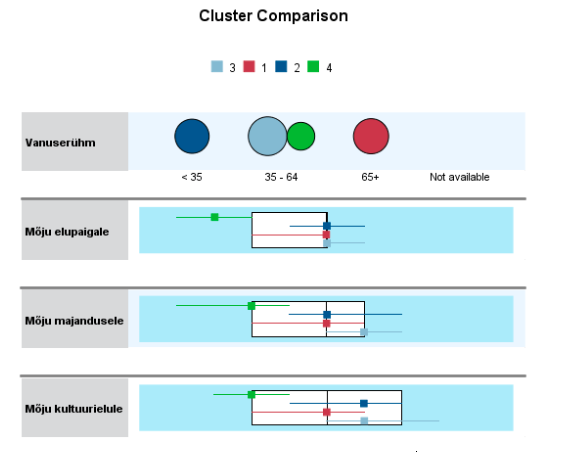
Joonisel 14 on kujutatud karpdiagrammide abil kõik neli klastrit. Vanuserühma (kategoriaalne tunnus) jaotus klastrite vahel näidatakse klastrile vastava ringi värvi ja suuruse abil. Näeme juba tuttavat pilti: noorim ja vanim vanuserühm jäävad kokku ja keskmine lahutub kaheks, suuremaks (helesinine ehk klaster 3) ja väiksemaks osaks (roheline ehk klaster 4). Üldise jaotuse karpdiagrammidelt näeme, et kultuurielule avalduva mõju hinnangud on teistest pisut suurema hajuvusega (karp kõige laiem, kvartiilhaare suurim). Elupaiga mõju hinnangu puhul langesid mediaan ja ülemine kvartiil kokku (pidev skaala, mida kasutasime täisarvuliste vastuste kujul).
Klastrite karpdiagrammi analoogideks on vastavat värvi horisontaaljooned alumise ja ülemise kvartiili kaugusel mediaani märkivast markerist. Rohelise klastri 4 (osa keskmisest vanuserühmast) hinnangud immigratsioonile on kõige halvemad. Järgmisteks võiks pidada punase klastri 1 liikmete hinnanguid (vanem vanuserühm) ja tumesinise klastri 2 hinnanguid (noorem vanuserühm). Suhteliselt veidi paremad on helesinise klastri 3 liikmete hinnangud (suurem osa keskmisest vanuserühmast). Järjekord ei ole muidugi väga selge ja erineb eri tunnuste puhul.
Klastrite tähenduse täiendamiseks anname nende iseloomustuse veel ka mõnede taustatunnuste poolest, milleks kasutame klasterduse käigus andmestikule lisatud klastrinumbrite tunnust.
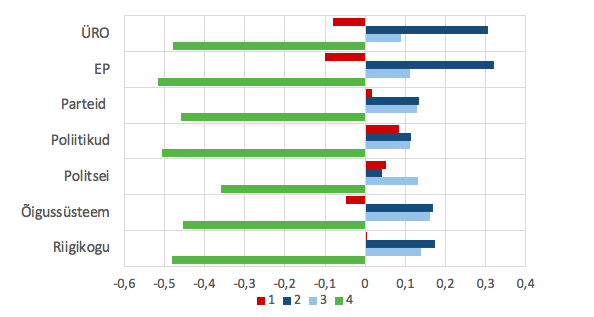
Joonisel 15 on näidatud eelmises, k-keskmiste meetodi osas tutvustatud poliitilise usalduse tunnuste standarditud väärtuste keskmised klastreis. Kasutatud on samu värve nagu klastrite võrdluses joonisel 14. Näeme neljanda (rohelise, immigratsiooni mõju suhteliselt halvemaks hindavate isikute) klastri liikmete keskmiselt teiste klastrite liikmeist madalamat usaldust poliitiliste institutsioonide suhtes. Ka esimese, vanema vanuserühma isikute klastri (punane) hinnangud olid pigem mõõdukad ja nad on poliitilise usalduse poolest keskjoonel või kohati alla-üle selle. Tumesinise ja helesinise klastri liikmete hinnangud immigratsiooni mõju suhtes olid pigem hea poole ja poliitiline usaldus ei jää alla keskmist. Näeme niisiis, et immigratsiooni suhtes positiivsemate hinnangutega kaasneb teataval määral suurem usaldus oma riigi ja tähtsate globaalsete institutsioonide vastu.
Selle peatüki otste kokkutõmbamiseks tegime veel ühe analüüsi, kus püüdsime võrrelda äsja kirjeldatud klasterdust samade tunnuste alusel k-keskmiste meetodil saaduga, kasutades seejuures vanust täisaastates, mitte vanuserühmi. Suhteliselt hea kokkulangevus tekkis k-keskmiste meetodi kolmeklastrilise liigitusega. Kolm klastrit k-keskmiste meetodil tulid (kokkuleppeliste nimedega) järgmised: 1 – suhteliselt vanemad ja mõõdukalt positiivsed (keskmine vanus 67, kolm hinnangut vastavalt 5,2, 5,5 ja 4,8), 2 – keskealised negatiivse hinnanguga (keskmine vanus 51, kolm hinnangut vastavalt 2,3, 2,5 ja 2,1), 3 – suhteliselt nooremad, positiivse hinnanguga (keskmine vanus 34, kolm hinnangut vastavalt 6,4, 6,7, 5,9). Kokkulangevused neljaklastrilise kahesammulise klasterdusega on näidatud tabelis 18 (kasutame ettevaatlikult ka nende klastrite puhul kokkuleppelisi nimesid).
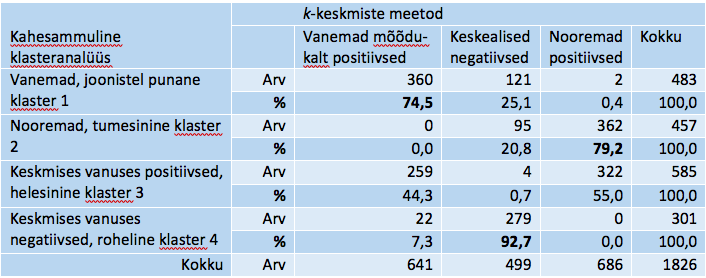
Selgelt eristus negatiivsete hinnangutega keskealiste isikute rühm, kus kahesammulise klasterduse vastavast klastrist kuulus 93% k-keskmiste meetodi analoogilisse klastrisse. Ka vanemaealiste suhteliselt mõõdukate hinnangutega indiviidide rühmad langevad kahes klasterduses suures osas kokku (75%). Samuti moodustavad nooremad positiivsete hinnangute indiviidid mõlemas klasterduses esiletuleva püsiva koosseisuga rühma (79%). Neljaklastrilise liigenduse „keskmises vanuses positiivsed“ jagatakse k-keskmiste meetodil laiali umbes pooleks k-keskmiste meetodi kahe rühma vahel. Kokkulangevusi on seega piisavalt ja erinevuste taga võib olla vanuse erisugune käsitlus kord vanuserühmana, kord täisaastates vanusena. Kui koostasime kahesammulise kolmeklastrilise täisaastates mõõdetud vanusega klasterduse, siis saime tõlgenduslikult samad klastrid nagu k-keskmiste meetodil, kusjuures individuaalne kokkulangevus ületas 80%, seega oli hea.
Allikaid ja lisalugemist
Bacher, J., Wenzig, K., Vogler, M. (toim.). (2004). SPSS TwoStep Cluster – a first evaluation. Nürnberg: Universität Erlangen-Nürnberg, Sozialwissenschaftliches Institut, Lehrstuhl für Soziologie. URL: http://nbn-resolving.de/urn:nbn:de:0168-ssoar-327153.
Choi, S.-S., Cha, S.-H., Tappert, C. (2010). A Survey of Binary Similarity and Distance Measures. Systemics, Cybernetics and Informatics, 8, 1, 43–48.
Desgraupes, B. Clustering Indices.
(https://cran.r-project.org/web/packages/clusterCrit/vignettes/clusterCrit.pdf; vaadatud 31.12.2019).
IBM Knowledge Center. Distancies. (https://www.ibm.com/support/knowledgecenter/SSLVMB_sub/statistics_mainhelp_ddita/spss/base/idh_prox.html; vaadatud 30.12.2019).
European Social Survey. (https://www.europeansocialsurvey.org/about/; vaadatud 30.12.2019).
IBM Knowledge Center. Hierarchical Cluster Analysis. (https://www.ibm.com/support/knowledgecenter/SSLVMB_25.0.0/statistics_mainhelp_ddita/spss/base/idh_clus.html; vaadatud 30.12.2019).
IBM Knowledge Center. k-Means Cluster Analysis. (https://www.ibm.com/support/knowledgecenter/en/SSLVMB_24.0.0/spss/base/idh_quic.html; vaadatud 30.12.2019).
Tooding, L.-M. (2015). Andmete analüüs ja tõlgendamine sotsiaalteadustes. 2. täiend tr. Tartu: Tartu Ülikooli Kirjastus, ptk 10.
IBM Knowledge Center. TwoStep Cluster Analysis. (https://www.ibm.com/support/knowledgecenter/kk/SSLVMB_24.0.0/spss/base/idh_twostep_main.html; vaadatud 30.12.2019).
Andmed
Valminud Hariduse Infotehnoloogia Sihtasutuse IT Akadeemia programmi toel.
