Kui faktoranalüüsi aluseks on tunnustevaheline korrelatsioonimaatriks, siis tekib küsimus, miks mitte selle hästi arusaadava kokkuvõttega piirdudagi. Vaatleme selle võimalikkust näite varal. Tabelites 1–5 on esitatud korrelatsioonimaatriksi andmed Euroopa sotsiaaluuringu viiest mõõtmisvoorust poliitiliste institutsioonide usaldusastme kohta Eestis, kokku igaühes seitse tunnust. Tunnuste tähenduse ja andmetega on võimalik tutvuda aadressilt http://www.yti.ut.ee/et/euroopa-sotsiaaluuring lähtudes. Võib arvata, et nendes hinnangutes peitub mingi üldisem vaade institutsioonidele, mis peegeldub korrelatsioonide mustris. Püüame seda mustrit üles leida ja „ilmutada“ need üldisemalt usaldust väljendavad omadused. Lugeja võib esmalt kõigi korrelatsioonimaatriksite detailse uurimise vahele jätta, piirdudes ainult ühega, nt 2012. aasta andmetega, ja tulla hiljem asjasse süvenenult tagasi. Sissejuhatuseks võiks jälgida ühe äramärgitud korrelatsioonikordaja ehk ühe tunnuspaari sisese seose muutusi aja jooksul.

Ülevaade faktoranalüüsist on üles ehitatud nii, et esmalt on päris pikalt esitatud põhimõtteid ja mõisteid ning näide nende kohta tuleb alles päris lõpus. Seepärast on soovitatav näiteni jõudmisel ja vastava mõiste kohaste arvude nägemisel lehitseda teksti ka ettepoole, et „teoreetilist“ osa veel kord üle vaadata. Näite sissepikkimine põhimõtetesse oleks lõppeesmärgi silme eest ära viinud ja selleni seletustes jõudmine oleks läinud väga pikale.

Sissejuhatuseks olgu öeldud veel see, et tänapäevased struktuurivõrrandite mudelid (vt nt Niels Blunchi „Introduction to Structural Equation Modeling Using IBM SPSS Statistics and Amos“, 2012 Sage Publ. Inc.) katavad suures osas tegevused ja ülesanded, mis moodustavad faktoranalüüsi ja selle rakendused, olles abiks veel palju laiemagi ülesannete klassi puhul. Faktoranalüüs sai alguse psühhomeetriast ja faktoranalüüsi peensusteni viidud parimad näited leiabki sellest vallast. Meetod on armastatud psühholoogias tervikuna.

Institutsioonide usaldusastme näide hõlmab seitsme tunnuse omavahelisi korrelatsioonseoseid viiel aastal. Tunnused on mõõdetud skaalal 0 (ei usalda) kuni 10 (täielik usaldus). See on väga mahukas info, mis ärgitab püstitama suurt hulka uurimisküsimusi. Milline on seose üldine tase ja kas see on aja jooksul nõrgenenud või tugevnenud? Mis hinnangud on omavahel tugevamini, mis nõrgemini korreleeritud? Kas usaldushinnangud on omavahel korreleeritud ühe ja sama mustri kohaselt, kui aastaid kõrvutada? Seda küsimuste rida võiks pikendada, kuid kõigile neile leiame omal kombel vastuse faktoranalüüsi kasutades. Uurige esmalt tabeleid 1–5 ja püüdke n-ö palja silmaga kujundada teatav arusaam usaldushinnangutevahelisest seosest. Paneme ka tähele, et kahjuks on korrelatsioonikordajale vastavas valimimahus päris suured kõikumised. See tekitab küsimuse, kuidas toimida edaspidi lünklike indiviididega. Et meid huvitavad hinnangud seitsme tunnuse alusel korraga, siis oleks põhimõtteliselt õigem piirduda nendega, kelle täielik seisukoht on teada. Teisalt kaotame niiviisi teatud hulga informatsiooni ja lisaks sellele tekib küsimus, kas andmeisse tekib seeläbi esindavuse nihe.

Tabel 1. Usaldus institutsioonide suhtes 2004. Allikas: Euroopa sotsiaaluuring 2004, Eesti

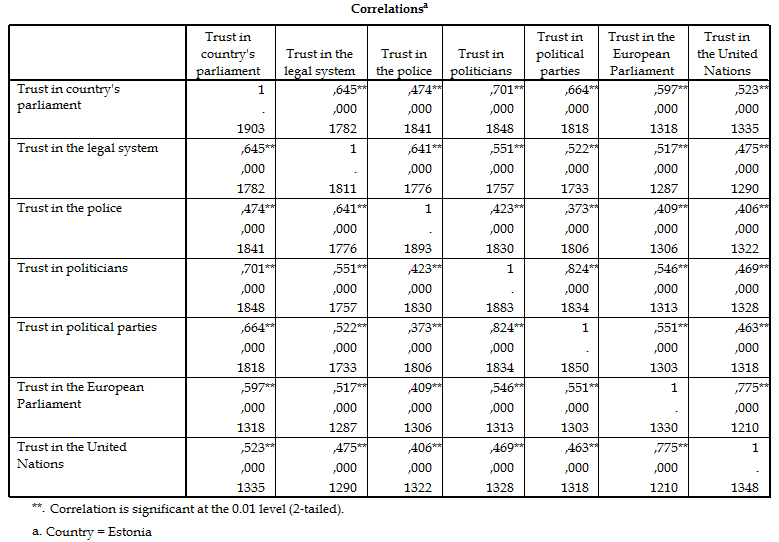
Tõlge: correlations – korrelatsioonikordajad, korrelatsioonimaatriks; correlation is significant at the 0,01 level – korrelatsioonikordaja on statistiliselt oluline olulisuse nivool 0,01.

Tabel 2. Usaldus institutsioonide suhtes 2006. Allikas: Euroopa sotsiaaluuring 2006, Eesti

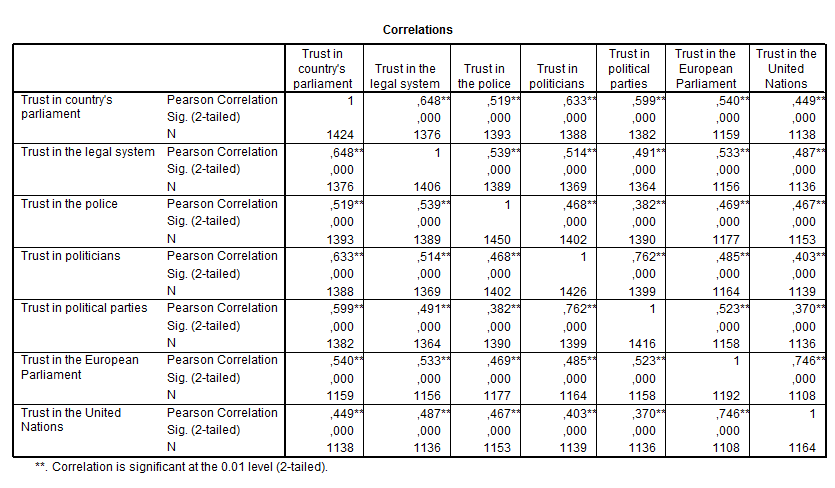
Tõlge: correlations – korrelatsioonikordajad, korrelatsioonimaatriks; correlation is significant at the 0,01 level – korrelatsioonikordaja on statistiliselt oluline olulisuse nivool 0,01.

Tabel 3. Usaldus institutsioonide suhtes 2008. Allikas: Euroopa sotsiaaluuring 2008, Eesti

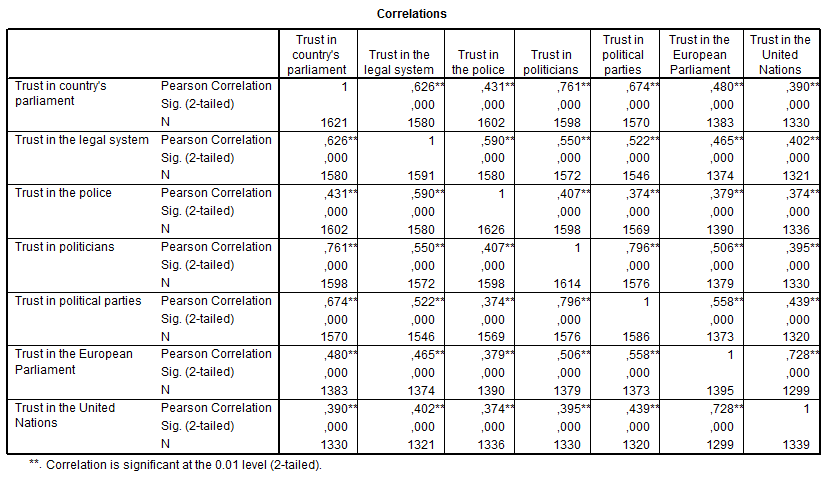
Tõlge: correlations – korrelatsioonikordajad, korrelatsioonimaatriks; correlation is significant at the 0,01 level – korrelatsioonikordaja on statistiliselt oluline olulisuse nivool 0,01.

Tabel 4. Usaldus institutsioonide suhtes 2010. Allikas: Euroopa sotsiaaluuring 2010, Eesti

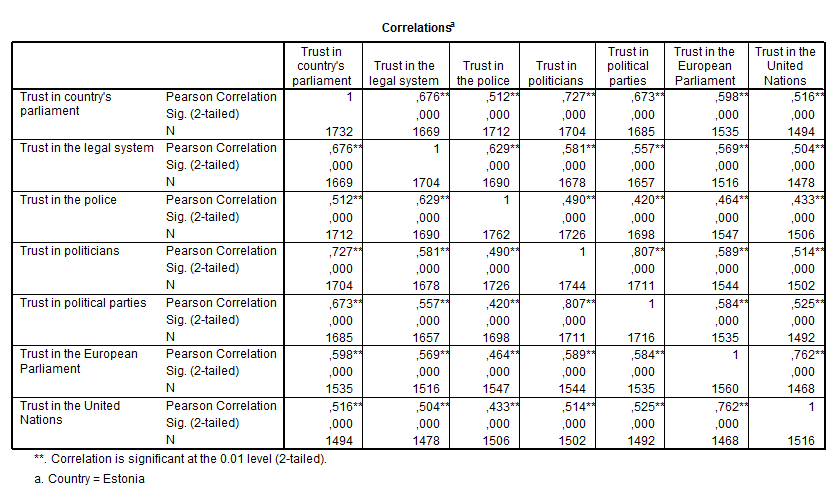
Tõlge: correlations – korrelatsioonikordajad, korrelatsioonimaatriks; correlation is significant at the 0,01 level – korrelatsioonikordaja on statistiliselt oluline olulisuse nivool 0,01.

Tabel 5. Usaldus institutsioonide suhtes 2012. Allikas: Euroopa sotsiaaluuring 2012, Eesti

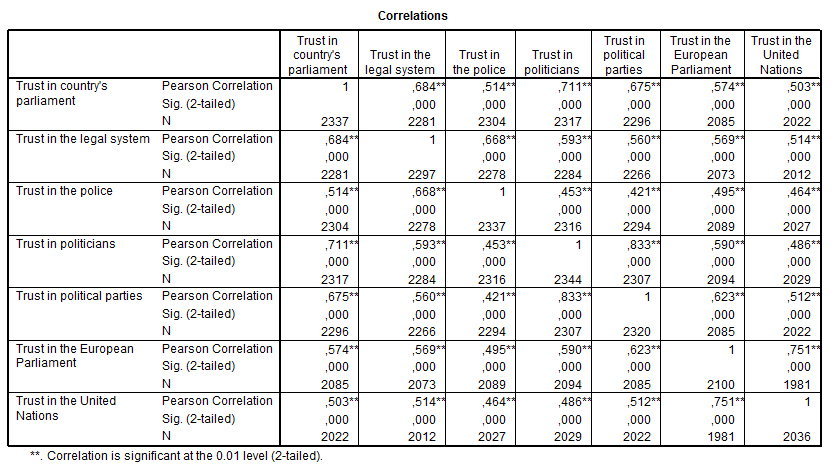
Tõlge: correlations – korrelatsioonikordajad, korrelatsioonimaatriks; correlation is significant at the 0,01 level – korrelatsioonikordaja on statistiliselt oluline olulisuse nivool 0,01.

Rakendame korrelatsioonimaatriksist ülevaate saamiseks üht ammust lihtsat visualiseerimise viisi – korrelatsioonigraafi. Selle tehnika on järgmine. Valime korrelatsioonimaatriksit silmitsedes mingi paraja küllalt kõrge korrelatsioonikordaja läve ja otsime välja kõik seda läve ületava seosetugevusega tunnuspaarid. Võtame tunnused graafi tippudeks ja kaared seosetugevuse märkimiseks. Joonistame võimalikult selge paigutusega tunnuseid ühendava graafi. Seejärel laseme korrelatsioonseose läve pisut allapoole ja lisame sellele tasemele vastavad tunnuspaarid graafi. Viime läve veel madalamale ja täiendame graafi seni, kuni pilt on veel enam-vähem selge. Võtame kokku üheks tunnusrühmaks omavahel enim kaartega ühendatud tunnused. Joonisel 1 on kujutatud usaldushinnangute seesugune liigitus 2004. ja 2006. aasta andmeil ning joonisel 2 2008. ja 2010. aasta andmeil. Korrelatsioonseose läveks on esmalt valitud 0,7 ja sellest tugevam seos valitses 2004. aastal poliitikute ja parteide, poliitikute ja Riigikogu ning Euroopa parlamendi ja ÜRO usaldushinnangu vahel. Ülejäänud kaks graafi tippu seisavad eraldi. Lävel 0,6 lisandub kaar parteide ja Riigikogu, õigussüsteemi ja Riigikogu ning õigussüsteemi ja politsei usaldushinnangute vahele. Veelgi jätkates joonistub välja kolm institutsioonide gruppi. Erinevate aastate graafe võrreldes näeme, et seoste struktuuris on päris suur analoogia. Püüdke 2012. aasta jaoks koostada seesugune graaf ise ja võrrelge eelnevate aastate andmetega.

Faktoranalüüsi aluseks on tingliku mittekorreleerituse idee. Tunnustest, mis uurimisobjekti tegelikult kirjeldavad, mõeldakse kahesugustena: mõõdetud tunnustena, mille väärtused on meil olemas, ja latentsete tunnustena, mis on seotud mõõdetud tunnustega ja kujundavad nende väärtusi, aga mida me ei oska otse mõõta. Mõõdetud tunnused olgu X₁, X₂, … X_p ja nende kaudu peegelduvad latentsed tunnused ehk faktorid F₁, F₂, … F_k, seejuures on latentseid tunnuseid tavaliselt vaatluse all märgatavalt vähem kui mõõdetuid: k << p. Mõõdetud tunnuste korral eeldatakse, et korrelatsioonseost tunnuste vahel saab „seletada“ faktorite kaudu (vasakpoolne skeem): korrelatsioonseos X_h ja X_i vahel r_hi tuleneb korrelatsioonseosest X_h ja F vahel ning X_i ja F vahel, i, h = 1, 2, … , p. Kui F on fikseeritud, siis ligikaudu r_hi = 0, mis tähendab tunnuste tinglikku mittekorreleeritust F suhtes (parempoolne skeem). Faktorite kaudu saab faktoranalüütilise idee kohaselt ammendavalt seletada mõõdetavate tunnuste vahel nähtuvaid seoseid. Kui faktoril ei ole variatiivsust, siis lakkab olemast meie vaate kohaselt seos tunnuste vahel.

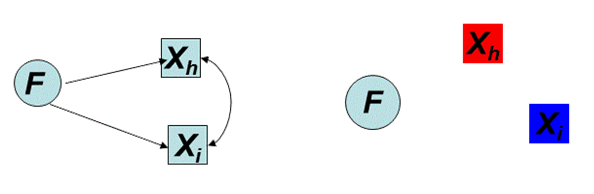
Latentsete tunnuste mõte on ainealane, teoreetiline mõte. Latentsete tunnuste olemasolu kinnitamine tuleneb uurija kontseptsioonist ja võib olla niihästi originaalne loogilis-teoreetiline idee kui ka juba eluõigust tõendanud ja tunnustatud vaade.

Faktoranalüüsi põhimudel seob mõõdetud ja latentsed tunnused järgmise skeemi kohaselt:

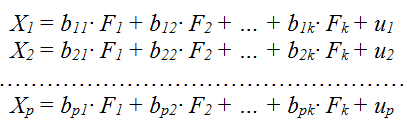
Tegemist on lineaarsete regressioonivõrrandite süsteemiga, kus sõltuvateks tunnusteks on mõõdetud tunnused ja seletavateks tunnusteks faktorid. Mudeli koostamine tähendab regressioonikordajate ehk faktorlaadungite leidmist teataval parimal viisil. Kasutatakse eriomaseid termineid:

• ühisfaktorid (seletavad tunnused on kõigile sõltuvatele tunnustele ühised) F₁, F₂, …, F_k , ingl common factors,
• omapäraelemendid (jäägid või vead, mis jäävad igast tunnusest „üle“, kui tunnuseid on väljendatud faktorite kaudu) u₁, u₂, …, u_p, ingl specific factors,
• faktorlaadungid (kordajad, mis väljendavad seda, kui palju „laadib“ iga faktor konkreetsesse tunnusesse variatiivsust) b_ij , ingl factor loadings.

Terve mõistuse kohaselt tundub, et heal lahendusel peaks olema vähe faktoreid, väikesed omapäraelemendid (vead) ja võimalikult suured laadungid. Allpool näeme, et mudeli põhiideest lähtudes (korrelatsioonseose ammendamine faktorite kaudu) tulenevad veel teatud spetsiaalsed lisaparameetrid mudeli iseloomustamiseks.

Faktoranalüüsi rakendatakse metodoloogiliselt kahes võtmes: eksploratiivse ehk kirjeldavana (otsingulisena) ja konfirmatiivse ehk kinnitavana. Mõlema eesmärgiks on tuua esile keskmiste ja kovariatsioonide kaudu tunnustevaheliste lineaarsete seoste parim võrgustik. Konfirmatiivse faktoranalüüsi korral antakse ette teatav kindel teoreetilisest kontseptsioonist lähtuv faktorlaadungite valik ehk määrang, millised faktorid milliseid tunnuseid laadivad (parempoolne skeem). Eksploratiivse faktormudeli korral on kõigi laadungite väärtused vabalt määrata (vasakpoolne skeem). Analüüs seisneb uurimises, kui hästi sobitub leitud mudel andmetega.

Tehniliselt tähendab faktorite „laadimismustri“ valik teatavate faktorlaadungite võrdsustamist mudelis nulliga. Eksploratiivse faktoranalüüsi mudelis loeme kõik faktorlaadungid vabadeks ehk andmetest tulenevateks, konfirmatiivse mudeli korral on vabad ainult teatavad meie poolt osutatud laadungid, ülejäänud „laadimisteed“ on kinni (nulltasemel). Konfirmatiivne mudel toetub veel tugevamalt kui eksploratiivne kindlale teoreetilisele alusele ja on seega küpse uurija meetod oma teoreetiliste visioonide empiiriliseks uurimiseks.

Kõigepealt nimetame matemaatilise järelduse, mis tuleneb tinglikust mittekorreleeritusest: osutub, et tehtud eeldustel lahutub mõõdetud tunnuse X_i, i =  1, 2, …, k dispersioon kaheks osaks — kommunaliteediks ja omapäradispersiooniks — ega ole seotud faktoritega:

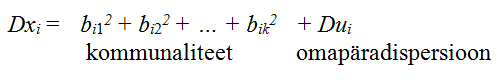
Omapäradispersioon on sisuliselt vea dispersioon ja väljendab seega lineaarsete võrrandite prognoositäpsust. Mida väiksem on vea dispersioon ja seega mida suurem on kommunaliteet ehk faktorite poolt tunnusest ühiselt ärakirjeldatud osa, seda parem. Samuti osutub, et esialgsete tunnuste X_i ja X_h, i, h = 1, 2, …, k vahelist kovariatsiooni (standardiseerimata korrelatsioon) saab avaldada faktorlaadungite kaudu (ja mitte vea kaudu):

                        cov (X_i, X_h) = b_i1 · b_h1 + b_i2 · b_h2 + … + b_ik · b_hk

            Veel järeldub, et omapäraelemendid u_i ehk vead ei ole omavahel korreleeritud ning omapäraelemendid u_i ja faktorid F_j , j = 1, 2, …, p ei ole omavahel korreleeritud (loomulikud ja head asjaolud). Faktorid leitakse tavaliselt omavahel mittekorreleeritutena. Need järeldused annavad aluse faktorlaadungite tuletamisele, mis ongi faktormudeli koostamise tehniliseks eesmärgiks.

Optimaalse faktorlahendi korral saavutatakse esialgsete tunnuste korrelatsioonseoste võimalikult täpne kirjeldamine (taastamine), faktorite kaudu arvutatud ehk mudelipärased korrelatsioonseosed tunnuste vahel on võimalikult lähedased esialgsetele. Faktori F_j kirjeldusaste avaldub faktoriga seotud faktorlaadungite ruutude summana:

                                     b_1j² + b_2j² + … + b_kj²

            Faktormudeli kirjeldusaste mõõdab, kui suurt osa algtunnuste summaarsest dispersioonist väljendavad kõik leitud faktorid koos. Faktormudeli kirjeldusaste avaldub üksikfaktorite kirjeldusastmete summana. Tunnuse kirjeldusastet väljendab kommunaliteet. Täiendava faktori lisamisel tavaliselt vähemalt mõnede tunnuste kommunaliteedid kasvavad ja ei kahane ka mudeli üldine kirjeldusaste. Millist kirjeldusastet lugeda piisavaks, on suhteline ja oleneb üldisest tunnuste seostuse astmest. Omavahel lõdvalt seotud tunnuste puhul võib ka näiteks 45% suurune kirjeldusaste olla empiiriline saavutus (kuigi pool variatiivsuse infost läheb kaotsi). Kõrge kirjeldusaste koos faktorite hea tõlgendatavusega on faktorlahendi soovitavad omadused. Kuidas aga tuleb mõista faktorit kui konstrukti sisuliselt?

Kui oleme faktorlaadungid leidnud ja faktorite kirjeldusastet piisavaks hinnanud, siis tekib küsimus, kuidas anda faktoritele meie uurimisobjekti seisukohalt teatav sisuline tähendus. Faktoritele tõlgenduse andmine on väga tundlik ja oluline etapp faktoranalüüsi käigus. Vaja on suurt enesekriitikat, head teoreetilise alusmudeli tundmist ja ettevaatust, sest esmane tõlgendus, kui ekslik see ka ei oleks, kipub pahatihti jääma lõplikuks.

Abiks on imepärane matemaatiline tulemus, mille kohaselt faktorlaadung b_ij osutub korrelatsioonikordajaks tunnuse X_i ja faktori F_j vahel, i = 1, 2, …, k; j = 1, 2, …, p. Faktori tähenduse määrab see tunnuste grupp, millel on suhteliselt suuremad faktorlaadungid selle faktori puhul. Tõepoolest, faktori nähtamatuks sisuks on see, millega ta on seotud nähtavate tunnuste maailmas. Uurija ülesandeks on anda vastus küsimusele, mis on see, mis on tugevalt seotud selle ja selle ja selle … mõõdetud tunnusega. Mida mõõdab niisugustes korrelatsioonseostes olev faktor?

Matemaatiliselt osutub, kui see faktori seletust lihtsustab, võib kõik faktorlaadungid ühe faktori piires muuta märgi poolest vastupidiseks (tähendab faktori sisulise suuna muutmist vastupidiseks, nt negatiivset mõõtvast positiivset mõõtvaks faktoriks). Mõnikord tuleb faktor tähenduse poolest ka bipolaarne: teatud tunnustega ilmneb positiivne, teatud tunnustega negatiivne korrelatsioonseos, osa tunnuseid suurenedes keskmiselt suurendab ja teine osa tunnuseid samal ajal keskmiselt vähendab faktori kui uue mõõdiku taset.

Faktorite tõlgendamisel on väga oluline analüüsida mõõdetud tunnuste tähendust ja ka seda, kuivõrd erisuguseid tähendusi võisid respondendid omistada vastamise käigus, milline võis olla nende tunnuste tõlgendus respondentide poolt. Mõnikord iseloomustatakse faktori sisemist tähenduslikku kooskõla suurematele faktorlaadungitele vastavate tunnuste Cronbachi kordaja varal (viide peatükile [Valiidsus ja reliaablus]) mis annab aimu saadud faktori sisereliaablusest.

Omaette küsimus on, millised laadungid (=korrelatsioonikordajad) lugeda suureks ja millised väikeseks. Ei poolda siinkohal lävesid, sest kõik on suhteline ja oleneb tunnuste seostuse üldisest astmest. Praktiliselt küllaltki vettpidavaks võiks lugeda tõlgendusskeemi, kus iga mõõdetud tunnust püüame määrata mingi faktori poolt laadituks (tunnuse suhtes suurima laadungiga faktor). Mõte on selles, et analüüsitavate tunnuste komplekt on eeldatavalt terviklik teoreetiline plokkskaala, mis peaks olema esitatav ühisfaktorite kaudu, ja kõik tunnused on ootuspäraselt tähtsad. Mõnikord aitab faktorite arvu suurendamine tõlgendust parandada, kuid mõnikord peab (raske südamega) mõnest tunnusest ka loobuma, et tõlgendus tuleks loomulik ja tõhus.

Faktoreid võime ette kujutada ka kui uut teljestikku meie uurimisobjekti kujutamiseks. Teljestiku tähenduse määrabki faktorite tõlgendus. Tõlgendada on sageli lihtsam, kui uus tõlgendusruum vanaga veidigi sarnaneb. Sel põhjusel orienteeritakse lihtsama tõlgenduse saamiseks faktorid kui uus teljestik esialgsete tunnuste ruumis ümber — pööratakse (ingl rotate). Kui näiteks lähme ruumis üle tasandile (nt laud toas kui toaruumi ammendava ärakasutamise vahend), siis paigutame selle ikkagi kas püsti või paralleelselt põrandaga ja mitte kuidagi viltu, et tekiks positiivne tunne laua kasutusväärtuse suhtes. Samasugune „tuttava suunas“ orienteerimise mõte on faktorite pööramise aluseks. Faktorite pööramine ei ole kohustus, vaid võimalus tõlgendust rikastada.

Matemaatiliselt tähendab pööramine teljestiku teisendust ehk teljekoordinaatide läbikorrutamist teatava teisendusmaatriksiga. Saab tõestada, et faktorlahend ongi määratud pööramise täpsusega, st teljestiku pööramise järel tekkiv teljestik rahuldab neid omadusi, mis teevad faktorist faktori faktoranalüüsi mõttes. Tuntakse mitmeid pööramisviise, sõltuvalt sihifunktsioonist (faktorite seletuse lihtsustamine, tunnuse seletuse lihtsustamine), sõltuvalt telgede omavahelisest asendist (ortogonaalne, kaldnurkne) jm alustel.

Sagedasim pööramisviis praktikas on varimaksmeetod, mis maksimeerib faktorlaadungite dispersiooni faktori piires. Pööratud faktorite faktorlaadungid on kontrastsed suuruse poolest — väikesed ja suured, keskmisi on vähe. See tähendab, et saavutatakse olukord, kus faktor on korreleeritud vähese arvu tunnustega, kuid tugevalt. Loomulikult on siis kergem seletada, mida faktor mõõdab, sest seoseid esialgsete tunnustega on vähe ja need on tugevad.

Pööramise käigus kommunaliteet ehk tunnuse dispersiooni kirjelduse aste ei muutu. Ei muutu ka mudeli summaarne kirjeldusaste, küll aga võib muutuda üksikfaktorite kirjeldusvõime ja loomulikult ka faktorite tõlgendus.

Ortogonaalsed pööramismeetodid, nt varimaks, kvartimaks, ekvimaks jt säilitavad faktorite ristseisu ehk omavahelise mittekorreleerituse. Kaldnurkse pööramise korral tekivad omavahel korreleeritud faktorid. Kaldnurkne pööramine võimaldab paremini edasi anda latentsete tunnuste kaudu reaalset omaduste struktuuri — tegelikus elus on muutujad omavahel pigem korreleeritud kui mittekorreleeritud. Siin on möödapääsmatu taas teha vihje suurele tänapäevastele lineaarsete mudelite klassile, nimelt struktuurivõrrandite mudelitele, mille erijuhuks on ka faktoranalüüs niihästi konfirmatiivsel kui ka eksploratiivsel kujul. Struktuurivõrrandite mudel on sisult regressioonivõrrandite süsteem, mis seob omavahel niihästi mõõdetud kui ka latentseid tunnused, võimaldades kõikvõimalikke korrelatsioone tunnuste vahel, sealhulgas faktorite vahel. Kaldnurkse pööramise vajadusel võikski pigem kasutada struktuurivõrrandite mudelit kui mõnd spetsiifilist kaldnurkset pööramismeetodit (oblimin, promaks jt).

Faktorite leidmise meetodite teema ei ole otseselt faktoranalüüsi rakendusvaldkonna uurija teema, sest matemaatiline külg on keerukas. Tuntakse arvukaid faktoranalüüsi meetodeid (puhtarvutuslikult). Vanimad ja eeskätt ajaloolist huvi pakkuvad, kuid käsitsi jõukohased on triangulatsioonimeetod (diagonaalmeetod) ja tsentroidmeetod. Sagedasim kasutuse poolest on peatelgede meetod (ingl principal axis factoring). Peatelgede meetodi praktiliseks alternatiiviks võiks pidada vähimjääkide meetodit (ingl minimum residuals method), mil optimeeritakse faktorlahend otseselt kovariatsioonide parima esituse seisukohalt, kaasamata tunnuste variatiivsuse edasiandmise kriteeriumi ehk kommunaliteete. Omaette ideestik on suurima tõepära meetodi (ingl maximum likelihood) aluseks — nimelt tõepärafunktsiooni maksimeerimine, kusjuures tõepärafunktsioon sõltub kovariatsioonistruktuurist, mida väljendatakse faktorlaadungite kaudu. Faktorlaadungid leitakse tingimusest, et tõepärafunktsiooni väärtus oleks suurim. Suurima tõepära meetodi korral tehakse ka teatavaid teste faktormudeli statistilise usaldusväärsuse hindamiseks, sest aluseks on valimi-üldkogumi kontseptsioon. Üldiselt aga välistab faktoranalüüs oma klassikalisel kujul valimi-üldkogumi teema, me lihtsalt uurime andmekogumit, ei kontrolli statistilisi hüpoteese ega hinda tulemuste statistilist usaldusväärsust (struktuurivõrrandite mudelite raames muidugi teeme seda). Huviline leiab teatava ajaloolise ülevaate nt allikast: Barbara G. Tabachnick ja Linda S. Fidell (2012)  „Using Multivariate Statistics“ (6th Edition), ptk 13.

Kui faktorid on latentsed tunnused, siis tekib mõte, miks mitte kasutada ka nende individuaalseid väärtusi. Uus integraalne tunnus, mis sest, et mitte 100%-lise võimega esialgset infot edasi anda, võiks olla väga kasulik. Seda mõnikord ka tehakse, kusjuures individuaalsed faktorite väärtused ehk faktorskoorid arvutatakse tavaliselt standardiseerituna, keskmisega 0 ja standardhälbega 1.

Väga ettevaatlik peab seejuures olema tõlgendamisega. Ahvatlev oleks võrrelda omavahel erinevaid gruppe nt keskmise paigutuse poolest faktori skaalal. Siin peab silmas pidama võimalust, et faktorstruktuur võib erinevates gruppides olla erisugune. Nt ühtede ja samade tunnuste puhul võib tunnuste seostuse muster olla madala hariduse grupis üks ja kõrge hariduse grupis teine. Ühises grupis saadud faktorid ei pruugi olla eraldi gruppides üldse faktoriteks siinkäsitletavas mõttes. Tekib küsimus, mille alusel meie võrdlus sel juhul toimub. Seega tuleks eelnevalt kontrollida faktorstruktuuri püsivust (invariantsust) grupilt grupile liikudes. (Siin pakub struktuurivõrrandite mudelite metoodika teatavaid lahendusi.) Kui oleks vaja kasutada individuaalseid väärtusi, siis võiks faktoranalüüsile eelistada peakomponentide analüüsi.

Asume nüüd saadud mõisteid rakendama institutsioonide usaldusastme näite korral. Esile toome kahe eri aasta tulemused, et suurendada usku faktoranalüüsi võimalikkusesse sisulise ülesande lahendamisel. Olgem ausad, raske on mõista, kuidas niivõrd formaalne matemaatiline algoritm võib anda sisuliselt tähendusliku lahendi. Aga nii see on ja on edukalt olnud juba aastakümneid – faktoranalüüs on metoodika, mis sai hoogsama arengu alates möödunud sajandi keskpaigast. Et vajalikud arvutused on mahukad, siis osutus arvutite tulek meetodi levikule väga soodsaks. Näites kasutame paketi SPSS väljundit, aga see on väga klassikaline ja samalaadne ka mujal.

Usaldushinnangud on keskmiselt erisugusel tasemel: korra ja õigusega seotud institutsioonidel kõrgemad, poliitikaga seotud küsimustes madalamad (vt tabel 6). Hinnangute standardhälve on 2–2,5 ringis.

Koostasime faktormudeli peatelgede meetodil pööramisega varimaksmeetodil, kasutades kaht faktorit. Selle esmapilgul arusaamatu lause püüame allpool näite varal avada. Alustame, nagu tavapraktikas, mudeli tõlgendust pööratud mudeli kujul (vt tabel 7).

Tabelis 7 on esitatud faktorlaadungid ehk korrelatsioonikordajad tunnuste ja faktorite vahel. Nii näiteks on 2010. aastal poliitikute usaldushinnangu faktorlaadung esimeselt faktorilt 0,87, mis tähendab, et mida suurem on faktori väärtus, seda suurem keskmiselt ka oli poliitikute usaldushinnang. Esimese faktori puhul on suuremad laadungid poliitikute, parteide ja Riigikogu usaldushinnangute suhtes, teise faktori puhul ÜRO ja Euroopa parlamendi usaldushinnangute suhtes. Õigussüsteemi ja politsei usaldushinnangute laadungid on enam-vähem ühesuurused mõlema faktori poolt, mistõttu nende kaudu faktorite tähendust ei saa selgelt määrata. Aastal 2008 on need kaks tunnust selgemalt laaditud esimese faktori poolt. Esimest faktorit võiks nimetada tunnuseks, mis mõõdab Eesti poliitiliste institutsioonide usaldust, teist tunnuseks, mis mõõdab globaalsete institutsioonide usaldust. Joonist 2 vaadeldes näeme graafi ja faktorlaadungite grupeerumisel suuruse järgi head kooskõla (kuigi graafi joonistasime kõiki indiviide kaasates, siinkohal vaid need, kes kõigile küsimustele vastasid). Nii see peakski olema, sest faktori juurde koonduvad „laadimiseks“ faktoriga tugevamalt seotud ja seeläbi ka omavahel seotud tunnused (meenutame eestpoolt faktoranalüüsi põhiideed tunnustevahelise seose ammendavast kirjeldamisest faktorite kaudu).

Vaatleme ka teist faktorite paari ehk pööramata lahendit (vt tabel 8). Pööramata lahend annab teistsuguse tähendusega faktorid: esimene faktor mõõdab usaldusastet üldiselt, eristamata, mille suhtes (telg „usaldab – ei usalda“). Teine faktor mõõdab eraldi usaldusastet ÜRO ja Euroopa parlamendi suhtes (positiivne korrelatsioon), vastandades neid poliitikute, parteide ja Riigikogu usaldushinnangule (negatiivne korrelatsioon). Seega võiksime öelda, et mida suuremad on teise faktori väärtused, seda keskmiselt madalam on usaldus omamaiste ja kõrgem usaldus globaalsete institutsioonide suhtes (ongi teatav bipolaarsus — „üks positiivne“ on võimendatud „teise negatiivse“ poolt). Pööramata lahendi puhul on faktorlaadungite „kontrastsus“ ühe faktori piires märgatavalt väiksem kui varimaks-meetodil pööratud lahendis, mil maksimeeriti faktorlaadungite dispersioon (sellest ka nimi varimaks — maksimeerida dispersioon, ingl variance).

Faktorlaadungite erisugusest suurusest tuleneb mõte, et tunnuste kirjeldusaste faktorite kaudu on erisugune: suuremate faktorlaadungitega tunnuste variatiivsus on edasi antud suuremas osas kui väiksemate faktorlaadungitega tunnuste variatiivsus. Tabelist 9näeme, et see mõte peab vett. Tabelis on esitatud tunnuste kirjeldusmäärad ehk kommunaliteedid arvudena 0 ja 1 vahel. Kommunaliteet peegeldab, kui suur osa tunnuse variatiivsusest (dispersioonist) on edasi antud faktormudeli abil. Kahe faktori abil on 2008. a andmeil suhteliselt paremini edasi antud ÜRO, poliitikute ja Riigikogu usaldusaste. Kaks aastat hilisemate andmete põhjal lisandub Euroopa parlamendi usaldushinnang. Kommunaliteet on arvutuslikult vastava tunnuse faktorlaadungite ruutude summa. Näiteks, poliitikute usaldusastme kommunaliteet 2010. aasta lahendis 0,839 saadakse summana 0,853² + (−0,334)² (tabeli 9 andmeil) või summana 0,866² + 0,299² (tabeli 8 andmeil).

Faktorlaadungite kaudu väljendub ka mudeli üldine kirjeldusaste, mis kujuneb üksikfaktorite kirjeldusastmete summana. Üksikfaktori kirjeldusmääraks on faktori kõigi laadungite ruutude summa. Tabelis 10 on osutatud, et meie näites on saavutatud 2008. aasta andmetel algtunnuste dispersiooni kirjeldus 64% ulatuses, sellest esimese faktori poolt 40% ja teise poolt 24% (arvud tabeli parempoolses osas). Kirjeldatust enam kui 60% ulatuses võib pidada heaks tulemuseks. Näeme, et pööramata lahendi puhul on kirjeldusmäärad teistsugused: 54% ja 10% (meid huvitanud bipolaarne faktor on üsna jõuetu). Pööramine muutis faktorite kirjeldusvõimet ühetaolisemaks, muutmata kogusummat. Aastal 2010 on saavutatud kahe faktoriga veel suurem kirjeldusmäär — 2/3 tunnuste koguvariatiivsusest.

Mis on tabelis 10 vasakul, seda on matemaatilise taustata raske seletada. (Faktoranalüüsi lahend põhineb korrelatsioonimaatriksi nn omaväärtusülesande lahendamisel, kusjuures omaväärtused peegeldavadki faktori kirjeldusastet ja omaväärtusele vastav omavektor osutubki faktoriks. Väga spetsiifiline!)

Faktoranalüüsi mõtteks on esile tuua ja võimalikult hästi edasi anda tunnustevahelise seose muster. Kui hästi õnnestus see meie näites ja kuidas seda üldse hinnata? Lihtne mõte on võrrelda tegelikke ja faktorite kaudu avaldatud (ehk mudelipäraseid) korrelatsioonikordajaid. Tabelis 11 näemegi 2010. aasta andmeil, kui hästi suutsime prognoosida usaldushinnanguis peituvat seost. Tabeli 11 ülesehitus on järgmine: ülemises plokis on näha korrelatsioonikordajate mudelipärased väärtused, kusjuures diagonaalil näeme kommunaliteete. Alumises plokis on näha tegelike ja mudelipäraste korrelatsioonikordajate erinevus ehk prognoosiviga ehk prognoosijääk. Miinusmärgiga jäägid kõnelevad seose ülehindamisest mudeli abil, positiivsed — alahindamisest. Kõige suurem prognoosijääk on tekkinud õigussüsteemi ja politsei usaldushinnangute vahelises seosekordajas. See ei üllata meid, sest just nende kahe tunnuse kommunaliteet oli madalaim (vt tabel 9). Ülejäänud prognoosijäägid erinevad nullist kuni 6-7 sajandikuni.

Faktoranalüüsi puhul tuleb teha mitmeid subjektiivseid otsustusi: tunnuskomplekti valik; indiviidigrupp, millel analüüsi teha; meetod, mille abil seda teha; kas pöörata mudelit või mitte. Üks olulisi otsuseid on ka see, mitut faktorit otsida. See otsus peaks esmalt põhinema sisulistel, teoreetilistel vaatekohtadel. Kui meil ei ole teoreetilist kontseptsiooni, mitu latentset tunnust võiksid kirjeldada uurimisobjekti ja mil viisil, siis ei saa ka tulemuses kindel olla. Paraku algetapil seda ettekujutust pahatihti ei ole ja seetõttu on kasutusel ka teatavad tehnilised kaalutlused. Öelda, et faktoranalüüs andis nii- või naapalju faktoreid, on vee segamine, sest alati vähem või rohkem kaudselt määrame me ise kriteeriumi, mitut faktorit võiks otsida.

Mis on need tehnilised oma valikute väljendamise vahendid?

• Faktormudeli soovitav kirjeldusaste; täiendav faktor ei langeta kirjeldusastet.
• Teatava tasemega kommunaliteetide saavutamine kõigi vaadeldavate tunnuste korral, täiendav faktor enamasti suurendab kommunaliteeti.
• Selle jälgimine, et kõigil faktoreil oleks suurem laadung mitme tunnuse suhtes korraga, et tekiks teatav integraalne uus dimensioon.
• Aluseks võetakse korrelatsioonimaatriksi juurde kuuluvad teatava matemaatilise definitsiooni kohased arvud — omaväärtused. Omaväärtuse suurus määrab omaväärtusele vastava faktori kirjeldusastme. Omaväärtusi leitakse nii palju, kui on algtunnuseid, ja nende summa võrdub tunnuste arvuga. Seega on keskmine omaväärtuse poolt määratud kirjeldusaste võrdne arvuga 1. Omaväärtuste suuruse kriteeriumiks võetaksegi mõnikord see, et kasutatakse nii mitut faktorit, nagu on keskmist kirjeldusastet ehk väärtust 1 ületavate omaväärtuste arv.
• Sõelatest (scree plot) ehk omaväärtuste graafiku tõusu kriteerium, mille puhul uuritakse omaväärtuste graafikut. Graafikul on horisontaalteljel omaväärtuse järjekorranumber suuruse poolest ja püstteljel omaväärtuse suurus. Kasutatakse nii mitut faktorit, nagu on omaväärtusi selgelt langeval omaväärtusi suuruse poolest ühendaval joonel (vt joonis 3). Näeme meie näite puhul, et viies erinevas andmestikus võiks kaks faktorit olla küllalt hästi sobiv lahend. (Kaks faktorit moodustab tasandi ja seda on alati hea graafiliselt kujutada uue teljestikuna.)

Faktorite arvu aitab mõnikord selgitada ka katse: kui arvame sobiva olevat nt kolm faktorit, siis uurime ka kahe- ja neljafaktorilist lahendit, hinnates tõlgendatavust ja kirjeldusastme erinevusi. Oluline on ka võrreldavus teiste samalaadsete töödega. Siiski — faktoranalüüs jääb oma põhiolemuselt siiski pigem kunstiks kui tehnikaks ja iga faktormudel, ka formaalsete parameetrite poolest kuitahes sarnane, on unikaalne.

Üks suuri segadusi faktoranalüüsis keerleb peakomponentide analüüsiga (ingl principal components) sarnasuse ümber. Need on kaks arvutuslikult lähedast ja tulemuste poolest samuti sageli lähedast mudelit. Põhiidee ja seega rakenduse eesmärk on neil kahel mudelil aga erisugused. Täpsemalt, aluseks olev informatsiooni kokkusurumise idee on erisugune.

Faktoranalüüsi puhul eeldatakse latentsete tunnuste olemasolu mõõdetud tunnuste väärtuste kujunemisel ja seatakse eesmärgiks nende leidmine ühisfaktoritena, mis haaravad võimalikult suure osa tunnuste ühiselt kirjeldatavast dispersioonist. Lähtutakse tunnuste tingliku mittekorreleerituse ideest ja saadakse faktorid sellistena, et tunnustevaheline korrelatsioon on võimalikult hästi edasi antud. Peakomponentide mudeli korral seatakse sihiks indiviide võimalikult hästi eristavate, st võimalikult suure dispersiooniga koondtunnuste saamine, mis haaravad võimalikult suure osa tunnuste kogudispersioonist. Omapäraelemente ehk mudeli vigu ei käsitleta.

Olgu vaatluse all omavahel vastastikku seotud arvtunnuste plokk X₁, X₂, … X_k. Esimene peakomponent C₁ leitakse kui lineaarkombinatsioon

C₁ = u₁₁· X₁ + u₁₂· X₂ + … + u_1k· X_{k ,}

mille kordajad määratakse nii, et peakomponendi dispersioon oleks suurim (indiviidide hajuvus on mõõtmes C₁ võimalikult suur ja indiviidid eristuvad üksteisest võimalikult selgelt). Teine peakomponent leitakse esimesega mittekorreleerituna (geomeetriliselt: ortogonaalsena), kusjuures selle kordajad määratakse nii, et teise peakomponendi dispersioon oleks suurim, st see haaraks tunnuste dispersiooni esimese peakomponendi poolt mittekirjeldatud osast võimalikult suure osa. Analoogiliselt tuletatakse ülejäänud peakomponendid, kusjuures neid võib moodustada sama palju kui tunnuseid. Sageli kasutatakse peakomponentidest vaid esimesi, mis definitsiooni kohaselt kirjeldavadki lõviosa tunnuste variatiivsusest.

Arvutusmeetodi poolest ühtib peakomponentide analüüs üldjoontes peatelgede meetodil läbiviidud faktoranalüüsiga. Lahendatakse korrelatsioonimaatriksi omaväärtusülesanne, kuid erinevalt faktoranalüüsist ei toimu peakomponentide laadungite iteratiivset parandamist kommunaliteetide suurendamise sihil. Peakomponentide kaalude tähendus on sama, mis faktorlaadungitel: korrelatsioonikordaja peakomponendi ja tunnuse vahel.

Peakomponente ei oleks vaja pöörata, sest see võib rikkuda nende esialgse tähenduse (tunnustest moodustatud suurima dispersiooniga lineaarkombinatsioon), kuid parema tõlgenduse huvides seda siiski vahel (isegi enamasti) tehakse. Peakomponentide kaudu saavutatakse üldiselt arvuliselt suurem üksiktunnuste kirjeldusaste kui sama faktorite arvuga faktoranalüüsis, sest modelleeritakse koguhajuvust, omapäradispersiooni kõrvale jätmata. Suurema kirjeldusastme numbri tõttu nähtavasti otsustavadki uurijad sageli pigem peakomponentide meetodi kui faktoranalüüsi kasuks☺.

Kaalutluse aluseks peaks siiski olema uurimisülesande sisuline külg. Kui soovime modelleerida seose struktuuri, siis kasutame faktoranalüüsi; kui soovime aga tuletada kokkuvõtvad indiviide hästi eristavad (indiviidide seisukohalt informatiivsed) uued tunnused, siis peakomponentide analüüsi.

Neljast tunnusest koosnev rahuloluhinnangute plokk — rahulolu eluga üldiselt, majanduse olukorraga, valitsuse ja demokraatia toimimisega — on Euroopa sotsiaaluuringu püsiplokk. Rahulolu mõõdeti skaalal 0 kuni 10 (rahulolematusest täieliku rahuloluni). Lisaks vaatleme hinnangut haridus- ja tervishoiusüsteemi olukorrale skaalal 0 kuni 10, kus 0 tähendab halba ja 10 head olukorda. Seame ülesandeks leida peatelgede meetodil kahefaktoriline faktormudel ja kahe peakomponendiga peakomponentide analüüsi mudel.

Peakomponentide analüüsi tulemused ja nende tõlgendamine on analoogilised faktoranalüüsi juhuga ja arvutiväljund tavaliselt samuti.

Tabelis 12 on võrdlevalt esitatud peakomponentide analüüsi (vasakul) ja faktoranalüüsi abil (paremal) saadud kommunaliteedid. Alglähendiks on peakomponentide analüüsi korral arv 1, faktoranalüüsi puhul teatav kommunaliteedi hinnang, mida parandatakse (suurendatakse). Kõigi tunnuste puhul on peakomponentide kaudu saavutatud tunnuse dispersiooni suurem kirjeldusaste kui faktorite kaudu. Kui peakomponentide kaudu on tunnuste kirjeldusaste 63% ja 74% vahel, siis faktorite kaudu märgatavalt varieeruvam: 34% ja 69% vahel. Madalaim on eluga üldise rahulolu kommunaliteet, mis viitab sellele, et see tunnus seostub ülejäänutega komplekti nõrgalt. Peakomponentide mudeli kirjeldusaste on suurem kui faktormudeli korral (vastavalt 70% ja 55%). Põhjus ikka sama — modelleerime üks kord kogudispersiooni, teine kord osa sellest ehk ühisfaktorite kaudu peegelduvat variatiivsust.

Peatelgede meetodil leitud faktorlaadungite ja peakomponentide laadungite muster suuruse poolest on niihästi pööramata (vt tabel 14) kui ka varimaks-meetodil pööratud kujul (vt tabel 15) üsna sarnane ehk siis peakomponentide tõlgendus on käesoleval juhul sarnane faktorite tõlgendusega. Niihästi esimene peakomponent kui ka esimene faktor mõõdavad rahulolu riigi toimimisega üldiselt ja ka oma eluga üldiselt. Teine peakomponent ja teine faktor mõõdavad haridus- ja tervishoiusüsteemi olukorra headust vastaja silmade läbi.

Laadungite muster on sarnane. Faktorite ja peakomponentide sisuline tõlgendus on sarnane. Tekib küsimus, millal saavutatakse suurem ja millal väiksem sarnasus kahe mudeli vahel. Põhiline erinevus tuleneb sellest, et faktorite leidmisel püütakse võimalikult täielikult haarata ühisfaktorite poolt väljendatavat variatiivsust, peakomponentide leidmisel aga koguvariatiivsust. Kui „ühisdispersiooni“ ja kogudispersiooni erinevus on väike (st tunnuste omapära on väike), siis ongi kokkulangevus parem. Teisalt, kui faktorstruktuur on väga selge ja saavutatakse esimeste iteratsioonidega (peakomponentide leidmiseks ei toimu tulemuse järkjärgulist parandamist), ka siis on kokkulangevus suurem.

Kui hea ettekujutuse saame peakomponentide kaudu tunnustevahelisest seosest? Vastus ei ole väga kiita (vt tabel 16). Leidub küllalt suuri prognoosijääke (tegelik korrelatsioonikordaja miinus peakomponentide kaudu prognoositud korrelatsioonikordaja) ja kolmveerand neist on suuremad kui 0,05. Siit paistabki kahe lähenemisviisi erinevus: peakomponentide mudel ei suuda seoste mehhanismi nii hästi peegeldada kui faktoranalüüs. Faktoranalüüsi mudelis käesoleva näite korral saime tühised jäägid ja mitte ükski neist ei ületanud arvu 0,05.

Faktoranalüüsi väljund on väga mahukas ja siin peab töö tegija alati lähtuma uurimisülesandest ja ka auditooriumist, kellele tulemusi esitletakse.

Keskmise teadmiste tasemega akadeemilisele auditooriumile tuleks tutvustada kasutatud tunnuste keskmisi ja standardhälbeid ning anda ülevaade korrelatsioonseoste suurusjärgust. Kindlasti tuleb nimetada indiviidide arv ja selgitada, kuidas käsitleti lünklikke indiviide. Kirjeldusastmed võiks nimetada teksti sees ja kommunaliteedid lisada faktorlaadungite tabelisse. Enamjaolt piisab pööratud mudeli esitamisest. Kusagil tekstis tuleb põhjendada faktorite arvu valikut. Faktoritele tuleks leida tabavad ja võimalikult täpsed nimed.

Laiale kuulajaskonnale võiks joonistada faktorite struktuuri näitava skeemi (faktorist suuremate laadungitega tunnusteni tõmmatud nooled, laadungi suurus noolele märgitud). Lisada faktoritele üldarusaadavad nimed.

Kõrgtasemel akadeemiline seltskond vaataks heal meelel ka jääkkorrelatsioonide jaotust ja pööramata faktorlahendit.

Tooding, L.-M. (2007). Andmete analüüs ja tõlgendamine sotsiaalteadustes. Tartu.  Ptk 7.2.

Richard Darlingtoni tekst http://www.psych.cornell.edu/darlington/factor.htm

SPSS rakendus http://www.ats.ucla.edu/stat/spss/output/factor1.htm