
Sotsiaalse Analüüsi Meetodite ja Metodoloogia õpibaas
Aegrea esmasanalüüs
Liina-Mai Tooding
2020
Kuidas kajastatakse andmeis aega?
Aeg on oluline näitaja sotsiaalses analüüsis – muutuja, mis võrreldes staatiliste andmetega ilma kahtluseta rikastab järeldusi, kuid samaaegselt lisab erinõudeid ning piiranguid andmeanalüüsi. Aega arvestatakse mõõtmisel mitmetel eri viisidel, nt teatud ajamomendil kirjeldatakse staatust (andmed üliõpilaste andmebaasis üliõpilase kohta: 2015–bakalaureuseõpe, 2016–bakalaureuseõpe, 2017–magistriõpe) või fikseeritakse teatud sündmuse toimumisel ajamoment (Mis kell algas intervjuu? Mis aastal asusite elama Elvasse?). Sageli vajatakse suhestamist teise ajamomendi või normiga (Kas kolisite Tartusse enne ülikoolis õppima asumist? Kas intervjuu toimus ennelõunal?). Suhestamise tulemuseks on sageli kestus (Kui kaua kestis intervjuu? Kui kaua enne sellesse elupaika asumist olite elanud Tartus?). Oluline kestuse tõlgendus on vanus.
Aja mõõtmine sotsioloogilistes andmetes toimub sageli omasuiste ütluste põhjal. See toob kaasa mitmed aja spetsiifikast tulenevad probleemid: ajaskaala on subjektiivne („hiljuti“ ei ole ühtmoodi määratletav), tõlgenduslik (vrd eri vanuses inimeste ajaperspektiivi), tänapäeval kõneldakse kiirenevast ajast ajadünaamika tajumisel. Ajaskaala on sageli suhteline.
Vaatleme põgusalt praktikas sagedamini esinevaid ajast sõltuvate andmete korrastamise viise.
Aegrida (ik time series) – aja jooksul muutuvate andmete rida. Üksiktunnust fikseeritakse paljukordselt teatud ajavahemike järel, mis sageli on võrdse pikkusega (aasta, tund, päev). Tüüpiliselt on korraga vaadeldavaid aegridu (tunnuseid) vähe. Uuritavast objektist tekib dünaamiline ettekujutus, kuid see on enamasti ühekülgne. Tähtis uurimisülesanne aegridade puhul on ajalise põhisuundumuse (trendi) kirjeldamine. Riiklik statistika esitatakse enamjaolt aegridadena.
Paneelandmestik (kordusmõõtmised; ik panel data, repeated measures) – tunnuseid mõõdetakse aja jooksul mitmel korral, kusjuures ajamomendid on valitud uuritavate isikute või objektide seisukohalt formaalselt, uurija tahte kohaselt. Indiviidide valik võib olla üks ja sama või erisugune, sageli on see osaliselt uuendatav teatud rotatsioonireegli kohaselt. Tunnuste valik on sama või osaliselt uuendatav. Tähtis uurimisülesanne on kirjeldada muutust teatud indiviidirühma tasandil. Selle andmestikutüübi näiteks sobivad Eesti sotsiaaluuringu andmed (Eesti sotsiaaluuring …) ja Euroopa sotsiaaluuringu andmed (European Social Survey …).
Longituudandmestik (ik longitudinal data) – tunnuseid mõõdetakse aja jooksul mitmel korral, kusjuures ajamomendid on valitud uuritavate isikute või objektide seisukohalt formaalselt. Indiviidide hulk on üks ja sama, mis võimaldab jälgida individuaalset dünaamikat. Spetsiifiliseks uurimisobjektiks on ühe indiviidi olekute, staatuste, arvandmete jm ajalises järjekorras olevad jadad, kuid oluline on ka indiviidirühmade kokkuvõtete vaatlemine. Tunnuste valik on sama või osaliselt uuendatav, sageli ka uurimiskonteksti muutuse tõttu, sest longituuduuring on tavaliselt pikaealine. Tähtis uurimisülesanne on muutuse uurimine indiviidi tasandil. Selle uurimisviisi näiteks on Eesti eluteeuuringud algusaastatega 1965 ja 1982 (uurimisrühma juht professor Mikk Titma; vt Titma 1999, Titma 2002, Kenkmann & Saarniit 1998) ja hilisematest praeguseni kestvatest töödest Eesti laste isiksuse-, käitumise- ja terviseuuring (ELIKTU, uurimisrühma juht professor Jaanus Harro, vt Harro jt 2015, vt ka ELIKTU kodulehte).
Kestust kajastavaid andmeid kogutakse sageli sündmuspõhiselt episoodide kaupa (ik events history data). Andmed fikseeritakse siis, kui meid huvitavate omaduste poolest on indiviidi olukorras toimunud teatav muutus (sündmus). Aega ja sündmust kirjeldavaid näitajaid mõõdetakse sündmuse toimudes. Joonisel 1 on toodud näide mõõtmisest episoodide kaupa, kus perioodi katmiseks läks vaja nelja episoodi, millest viimane lõpeb uuringu lõpu, mitte uue sündmusega.
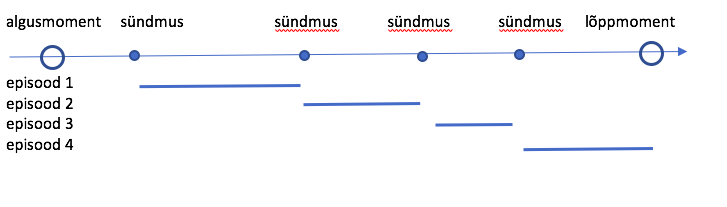
Eri liiki sündmustest (töökoha omandamine, perekonnasündmus, palgamuutus, elukoha muutus jne) kujunevad eri liiki episoodide jadad. Sündmuste analüüsis (ik event history analysis) tegeldakse episoodi pikkuse modelleerimisega. Meetodi lähteks on biomeetriast pärinev eluea analüüs (elukestusanalüüs, elulemisanalüüs, ik survival analysis) ja sündmuste analüüsi laiem levik sotsiaalteadustes algas möödunud sajandi viimases veerandis (Tuma 2004).
Selles tekstis vaatleme lähemalt aegrida, piirdudes esmasanalüüsi võtetega aegrea analüüsimisel. Näited on koostatud paketi SPSS abil ja osutatud ka, mis võimalused on paketis SPSS aegridade esmasanalüüsiks. See ei kata selle paketi aegridade analüüsi kõiki võimalusi.
Aegrea määratlused eri sõnastuses „ajast sõltuvate vaatlustulemuste kogum“, „nähtuse ajalist muutumist iseloomustavate arvandmete rida“, „üksteisele järgnevatel ajaintervallidel/ajamomentidel mõõdetud väärtuste rida“ jt sisaldavad kolme aegridade omadust: mõõtmiste järgnevus üksteisele ja sageli ka ühesugused ajavahed, (enamjaolt) arvulisus ning püsiv mõõtmisviis ja mõõtmistingimused. Formaalses tähistuses on aegrida indeksiga varustatud mõõtmiste xt, t = 0, 1, 2, …, n jada x0, x1, …, xn, mille üksikmõõtmist nimetatakse aegrea liikmeks või aegrea olekuks. Indeksit nimetatakse enamasti ajaks, kuigi selle tähenduseks võib olla ka mõni muu järgnevust määrav näitaja (nt kaugus täiskilomeetrites Tallinnast). Kui aja ühikuks on üksikmoment, siis kõneldakse vahel momentreast, kui ajavahemik, siis vahemikreast.
Joonisel 2 on kujutatud Eesti rahvaarvu aegrida sajandipikkusel perioodil. Aegrea kulg on mitmekesine: suhteline stabiilsus kuni Teise Maailmasõjani, katkemine, ligikaudu lineaarne tõus möödunud sajandi 90. aastateni ja seejärel mittelineaarne langus stabiliseerumise või koguni tõusu märkidega.
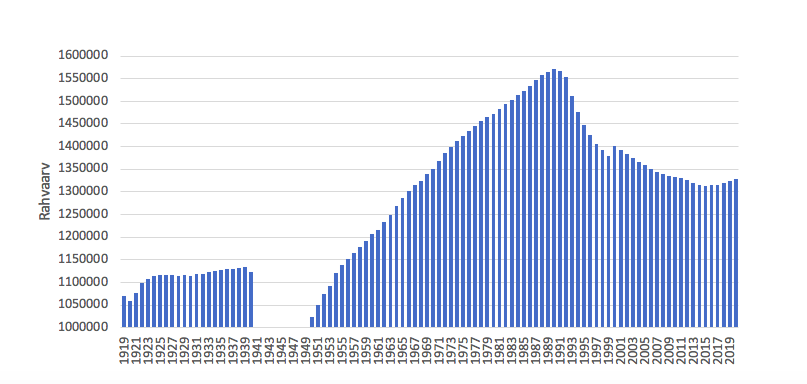
Rahvaarvu aegrea detailsemaks kirjeldamiseks peaksime seda analüüsima osade kaupa, sest eri osadel on erinev iseloom. Ka on selge, et mõisted, mille abil nendest osadest kõnelda, peaksid olema erinevad: alguses teatavast rahvaarvu tasemest ja kõikumisest selle ümber, seejärel kasvu/kahanemise kiirusest ja laadist.
Aegreas eristatakse kolme osa:
et – juhuslik komponent ehk müra (ik random component, noise),
Tt – trend ehk suundumus, süstemaatiline osa (ik trend),
St – sesoonne osa, perioodiline osa (ik seasonal variation component).
Peale nende eristatakse pikemaajalisi vähem selgeid kordusi tsüklitena (ik cyclic variations), nt majanduse arengutsüklite näol.
Aegrea analüüs seisneb selle osade eritlemises. Osade kaudu võib aegrida vaadelda aditiivsena (liituvana):
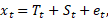
või multiplikatiivsena (korrutisena):
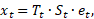
mis logaritmides annab aditiivse mudeli:
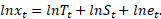
Korrutismudel sobib, kui aegrea osad on omavahel seotud, nt sesoonne osa on võrdeline trendiga. Kõiki osi ei pruugi aegreas alati leiduda. Aegrea analüüsi ülesanded on (1) aegrea osade kirjeldamine, sh väga sageli graafiliselt, (2) ilmnenud suundumuste seletamine kas mõne teise aegrea või tõlgenduslikult taustateabe abil, ja (3) võimaluse korral aegrea edasise kulu prognoos. Prognoosi võimalikkuse määrab see, kuivõrd püsiv on suundumus aegreas.
Vaadeldavas rahvaarvu näites on selgelt olemas trendi sisaldavad perioodid (1950–1990, 1990–2015) ja samuti juhuslik komponent, kuid sesoonsust ja tsüklilisust ei ole märgata. Vaatlemegi allpool seda aegrida eraldi perioodidena, kus vaja läheb eri liiki analüüsivõtteid. Selle aegrea puhul on ilmekalt näha elementaarne põhimõte, mida peaks järgima aegrea graafiku joonistamisel: aeg peab kulgema ühetaoliselt, järjest. Ettekujutus rahvaarvust oleks hoopis teine, kui sõja-aastad vahel jätta. Seda vaevalt siin keegi teeks, aga mõne vähemnähtava katkestuse korral võiks nii juhtuda.
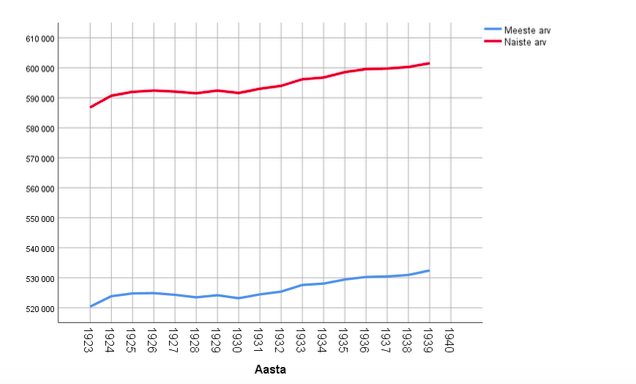
Vaatleme, milliseid aegrea statistilisi kokkuvõtteid võiks tuua esile siis, kui aegrida kulgeb ajas suhteliselt stabiilselt, kindla suundumuseta. Näitena kasutame rahvaarvu perioodil 1923–1940, mis on kujutatud joongraafikuna joonisel 3 eraldi meeste ja naiste arvuna (1940. aasta andmed rahvaarvu kohta olid osutatud allikas olemas, aga naiste ja meeste kohta eraldi mitte). Jätsime selles alaosas oma väärtuslikust andmebaasist perioodi algusaastad 1919–1922 kõrvale sellepärast, et neil aastail toimus märgatav rahvaarvu kasv, aga näitajad, mida soovime vaadelda, eeldavad võimalikult püsivat aegrida.
Jooniselt 3 nähtub, et ka sel perioodil on aegreas kasvav suundumus, kuid nõrgalt, 12–15 tuhande inimese piires. See õigustab perioodi kokkuvõtet keskmiselt.
Kui eeldada aegrea püsivat taset ja trendi puudumist, siis saab esitada aegrea kokkuvõtte keskmise ja standardhälbe kaudu. Kui on antud aegrida x0, x2, …, xt, …, xn, siis selle aegrea aritmeetiliseks keskmiseks on m, mis leitakse valemist
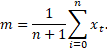
Vajadusel võib ajamomentidele lisada sisuliselt põhjendatud kaalud ja kasutada kaalutud keskmist. Eelnev valem on vahetult rakendatav diskreetsete ajamomentide jaoks. Kui aega käsitletakse pideval skaalal, siis võib aegrea keskmise (nimetatakse ka kronoloogiliseks keskmiseks) leida aegrida ühepikkusteks perioodideks jagades perioodikeskmiste keskmisena.
Mõnikord vaadeldakse tsentreeritud aegrida: elementide xt asemel rida elementidest xt – m, t = 0, 1, 2, …, n. Selline aegrida näitab olekuid keskmise oleku suhtes. Aegrea dispersiooniks on tsentreeritud väärtuste ruutude keskmine ja standardhälbeks s ruutjuur sellest:
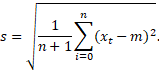
Aegrea keskmise püsivuse mõte seondub aegrea statsionaarsuse mõistega, mis tähendab üldjoontes seda, et aegrea omadused aja jooksul ei muutu. Tuntakse mitmeid statsionaarsuse määratlusi, olenevalt sellest, kui rangelt omadusi piiritletakse: nt eeldades, et keskmine ja dispersioon jäävad püsivaks aegrea eri lõikudel, või eeldades, et aegrea elementide jaotus on püsiv (vt huvi korral lähemalt matemaatilist käsitlust Kangro 2016, ptk 3). Need on teoreetilised eeldused, mille alusel on välja arendatud aegridade mudelid, sh aegridade prognoosimiseks.
Tabel 1. Rahvaarv Eestis aastatel 1923–1940, tuhandetes

Tabelis 1 on esile toodud perioodi 1923–1940 keskmine rahvaarv ja selle standardhälve. Mehi on sel perioodil keskmiselt 68,3 tuhande võrra vähem kui naisi. Naiste arv on sel perioodil kasvanud perioodi algusega võrreldes enam kui meestel (vt haaret, sest vähim rahvaarv oli perioodi alguses ja suurim lõpus), mida kinnitab ka suurem standardhälve. Sõjaeelsel perioodil oli aastakeskmine naiste arv 660 tuhat ja meeste arv 530 tuhat.
Kuidas joonistada paketis SPSS aegrea graafikut aegrea analüüsi erivõtete abil?Kui aegrida ei ole püsiv, siis tekib vajadus kirjeldada selle muutust. Praktikas on selleks kasutusel mitmeid intuitiivselt hästi mõistetavaid näitajaid, millest allpool vaatleme kesksemaid. Lisalugemist on rohkesti võimalik leida igast majandusstatistika käsiraamatust (Sauga 2019, 2017, rohkesti näiteid; Paas 1995).
Absoluutne juurdekasv (ik difference, growth) dt ajamomendil t on käesoleva oleku xt ja eelmise oleku xt-1 vahe: dt = xt – xt-1, , t = 1, 2, …, n. Absoluutne (mittesuhteline) juurdekasv näitab, kui palju erineb aegrida antud ajamomendil aegrea väärtusest eelmisel ajamomendil. Negatiivne juurdekasv tähendab aegrea kahanemist ja positiivne kasvu. Nulljuurdekasv tähendab püsivat aegrida. Absoluutse juurdekasvu mõõtühik on sama mis aegreal. Absoluutsetest juurdekasvudest tekib omakorda aegrida (ühe elemendi võrra lühem kui algne aegrida – esimesel liikmel ei ole eelnevat liiget), mida võib vajadusel analüüsida nagu tavalist aegrida.
Kasvutempo (ahelindeks) kt ajamomendil t saadakse aegrea antud väärtuse jagamisel eelmise väärtusega; kt = xt / xt-1, kus xt on n ajamomendi aegrida, t = 1, 2, …, n. Arvust 1 väiksem kasvutempo tähendab kahanemist, arvust 1 suurem kasvutempo kasvu ja arvuga 1 võrduv kasvutempo aegrea püsivust antud ajamomendil. Kasvutempo näitab, kui mitu korda ületab antud väärtus eelmist (kasvamisel) või kui suure osa moodustab eelmisest (kahanemisel). Kasvutempode väärtustest moodustub omakorda aegrida, mida võib analüüsida tavapärasel viisil. Lisame, et keskmise kasvutempo arvutamisel kasutatakse tavaliselt geomeetrilist keskmist:
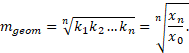
Eelneva võrduse viimane osa tuleb lihtsalt välja, kui panna kasvutempo asemele avaldis aegrea liikmete kaudu.
Suhteline juurdekasv ehk juurdekasvutempo (ik growth rate) on antud ajamomendi absoluutse juurdekasvu suhe aegrea eelmise ajamomendi liikmesse: at = dt / xt-1, t = 0, 1, 2, …, n. Lihtne algebraline arvutus võimaldab näidata, et juurdekasvutempo avaldub kasvutempo kaudu järgmiselt: at = kt – 1. Kui kasvutempo on 1, siis on juurdekasvutempo 0. Kui juurdekasvutempo on positiivne arv, siis juurdekasvutempo näitab mitmendiku võrra aegrea liikmest eelmisel ajamomendil aegrida kasvas. Kui juurdekasvutempo on negatiivne, siis juurdekasvutempo näitab, mitmendiku võrra aegrea liikmest eelmisel ajamomendil aegrida kahanes. Suhtelist juurdekasvu väljendatakse sageli protsentides.
Sageli vaadeldakse aegrea muutust teatava alusajamomendi suhtes (jaanuar, I kvartal, perioodi algusaasta, parim aasta jne). Sel juhul asendatakse eelnevates mõistetes eelmine ajamoment alusajamomendiga ja kõneldakse vastavalt alusjuurdekasvust (ik base growth), aluskasvutempost (alusindeksist) ja suhtelisest alusjuurdekasvust ehk alusjuurdekasvutempost (i.k. base growth rate). Alusjuurdekasv näitab aegrea antud momendi liikme erinevust alusmomendi liikmest. Aluskasvutempo näitab, kui mitmekordne on aegrea liige käesoleval momendil võrreldes alusmomendiga või, negatiivse kasvutempo korral, kui suure osa moodustab aegrea liikmest alusmomendil. Suhteline alusjuurdekasv näitab, kui suure osa võrra alusmomendi liikmest on aegrea käesoleva momendi liige suurem (või väiksem negatiivse aluskasvutempo korral) alusmomendi liikmest.
Tabelis 2 on toodud kahe näite korral eelnevate mõistete kohaseid arvutusi (n = 4, viie ajamomendi kasvav ja kahanev aegrida). Juurdekasvu, kasvutempot ja juurdekasvutempot võib iseloomustada kui ahelindikaatoreid, sest arvutuse alus nihkub aegrea iga liikme korral.
Tabel 2. Näiteid aegrea muutust kirjeldavate statistikute kohta
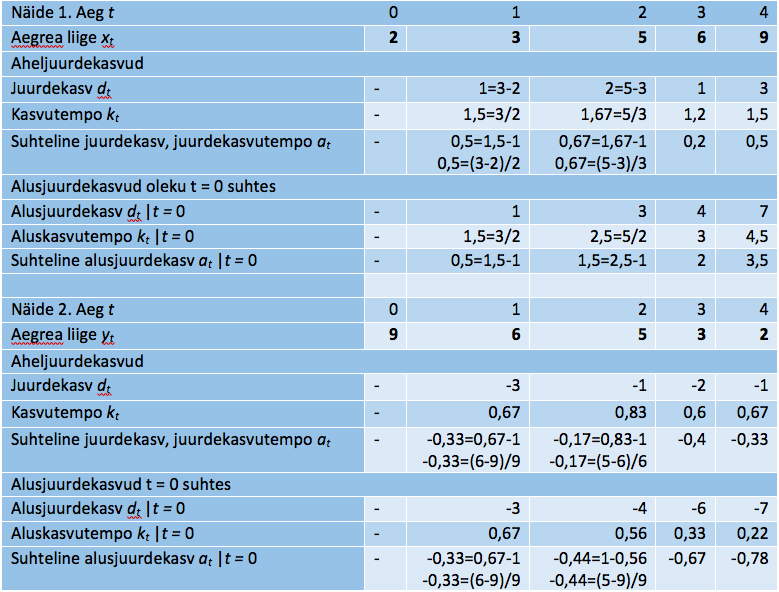
Esimese aegrea geomeetriline keskmine kasvutempo on 1,457 ja teise aegrea geomeetriline keskmine kasvutempo (st kahanemistempo) on 0,69.
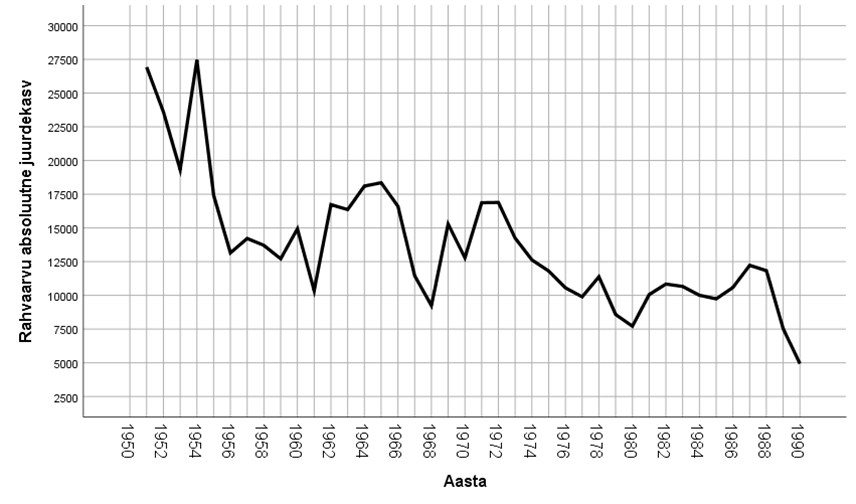
Pöördume tagasi rahvaarvu näite juurde ja vaatleme, kuidas esitatud mõistete abil iseloomustada Eesti rahvaarvu muutust perioodil 1950–1990. Uurime esmalt, milline näeb välja absoluutsete juurdekasvude aegrida, mille moodustame esialgsest aegreast liikmete järjestikuse lahutamise teel (paketis SPSS on ulatuslikud võimalused aegridade teisendamiseks, vt vastavat tekstikasti). Rahvaarvu juurdekasv on kuni 1955. aastani kiire, sealt edasi jääb 10–18 tuhande piiresse ja alates 1975. aastast kümne tuhande ümbrusse (joonis 4). Kui perioodi algusaastad kõrvale jätta, siis võiksime kõnelda perioodi keskosas suhteliselt püsivast ning alguses ja lõpus aeglustuvast juurdekasvust. Sama järelduse saame teha rahvaarvu kasvutempo vaatlemisel (joonis 5), aga teisest vaatenurgast.
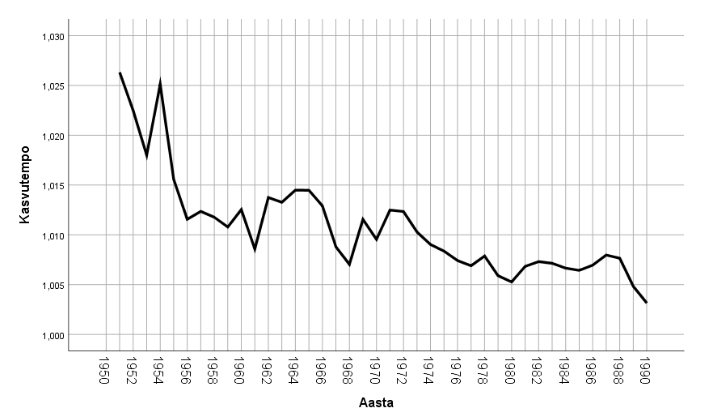
Rahvaarvu kasvutempo on vaadeldaval perioodil vahemikus 1,005 kuni 1,025, st iga järgnev aasta ületab eelmise (sama väljendasid positiivsed juurdekasvud joonisel 4). Juurdekasvutempo langeb alates 1955. aastast ja jääb aja jooksul kergelt vähenedes 0,5% ja 1,5% vahele (meenutame: kasvutempo miinus 1, väljendatud protsentides).
Aegrea süstemaatilise osa – trendi – teadmine võimaldab aegrea kompaktset kirjeldust matemaatilise funktsiooni kujul ja selle kaudu ka teatud ulatuses ennustada aegrea tulevast käiku. Trend peegeldab formaliseeritud kujul aegrea sõltuvust ajast. Praktilistel kaalutlustel on alati mõistlik eelistada sobivatest trendi kirjeldavatest mudelitest võimalikult lihtsat. Trend on ligilähedane aegrea esitus ja seepärast tuleks trendi täiendavalt iseloomustada ka täpsuse poolest, nt vastava matemaatilise funktsiooni kirjeldusastme kaudu (kui suure osa aegrea hajuvusest kirjeldab valitud lähendfunktsioon, kasutada determinatsioonikordajat aja seisukohalt). Trendi kirjeldamise ülesanne on lahendatud ka sel juhul, kui trendi eritleda ei õnnestu, sest igas aegreas ei pruugi trendi olla. Õigemini, trend on sel juhul ajast sõltumatu konstandiga (aegrea keskmine) võrduv funktsioon.
Millest kõneleb see, et rahvaarvu näites vahede aegrida aastatel 1950–1990 (joonis 4) on vähemalt ositi suhteliselt püsiv? Sellest, et rahvaarvu selle perioodi aegrida on vähemalt ositi võimalik küllalt hästi kirjeldada lineaarse trendiga. Tõepoolest, kui aegrea trend avaldub aja suhtes lineaarselt ja iga t korral kehtib seos
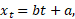
kus a ja b on sobivalt leitud parameetrid, siis vahe dt on püsiv:
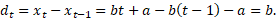
Lineaarse trendiga aegreas on juurdekasv püsiv.
Vahede aegrea koostamine on lihtne võte trendi eemaldamiseks. Kui järele jääb juhuslik aegrida nullmürataseme suhtes, siis võib järeldada, et lineaarne trend on aegrea hea iseloomustaja. Seejärel tasub uurida lähemalt, missuguse matemaatilise võrrandiga on see trend.
Kui vahede rida ei ole püsiv, siis tasuks edasi uurida teist järku vahede aegrida ehk vahede vahedest moodustatud aegrida. Kui see on püsiva käiguga, siis võiks olla heaks trendi lähendiks ruutfunktsioon (selle põhjendus on analoogiline äsjatoodule, ainult algebraliselt natuke tülikam). Ruuttrendi
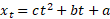
korral ei ole juurdekasv (aegrea muutuse „kiirus“) püsiv, vaid sõltub ajast ja ruutliikme kordajast c. Juurdekasvude väärtustest moodustatud aegrea juurdekasv (aegrea muutuse „kiirendus“) on ruuttrendi korral püsiv.
Aegrea lähendkõverat sobitatakse praktikas ajast sõltuvuse lähendfunktsioonide laiast hulgast, mitte üksi polünoomidena aja suhtes, nagu äsja vaatlesime (nt eksponentsiaalne sõltuvus ajast, logaritmiline trend). Tabav lähendfunktsiooni valik on hea sobituse alus. Heaks abiliseks mudeli valikul on sageli aegrea diagramm, millelt tuleb otsida sarnasust mõne matemaatilise funktsiooni graafikuga. Loomulikult on vaja sisuliselt mõista modelleeritavat protsessi. Nagu juba eespool öeldud: kasutada nii lihtsat funktsiooni kui võimalik, aga loomulikult olenevalt ka trendi leidmise eesmärgist. Üldise suundumuse selgitamisel on lihtne ajast sõltuvuse reegel parem kui suure täpsusega keeruline mudel, kuid näiteks füüsikalise katse tulemusi kirjeldades või majandusprognoosi korral jääks sellest võib-olla vajaka.
Naaseme rahvaarvu muutuste juurde aastatel 1950–1990. Kui hoolikalt vaadelda joonist 2, siis on näha ka teatavat kõrvalekallet (kumerust) hüpoteetilisest sirgjoonelisest rahvaarvu kasvust. Seepärast sobitame vastava aegrea trendina sirge kõrval ka teisi funktsioone. Kuidas seda teha paketi SPSS vahenditega, on kirjeldatud vastavas tekstikastis.
Tabelis 3 on esitatud tuhandetes väljendatud rahvaarvu lineaarse mudeli kohased tabelid paketi SPSS kasutamise tulemusena. Aega arvestatakse aasta järjekorranumbri kaudu alates 1940. aastast. Tulemused on esitatud kohati liiga suure täpsusega, aga nii on lugejal võimalik soovi korral kaasa arvutada. Tabeli 3 esimene osa sisaldab trendi sobitusastet iseloomustava mitmese korrelatsioonikordaja aja suhtes (R, ik multiple correlation coefficient) ja selle ruudu (determinatsioonikordaja, ik determination coefficient, R square); korrigeeritud väärtus arvestab mudelis olevate tegurite arvu, praegu vabaliige ja aeg ning väärtus praktiliselt ei muutu). Determinatsioonikordaja on 100% lähedal, mis kõneleb väga hästi sobituvast trendist. Ka hinnangu standardhälve ei ole aegrea liikmete suurusjärku (rahvaarv tuhandetes) arvestades suur.
Tabeli 3 teise osa moodustab klassikaline dispersioonalüüsi tabel, milles näidatakse trendi lahknevust aegreast liikmeti summaarse ruuthälbe osadena: trendi poolt kirjeldatud osa (regressioon, aegrea avaldis aja kaudu) ja jääk (trendi poolt kirjeldamata osa). Determinatsioonikordaja näitab trendi abil kirjeldatud osa suhet kogu hälbesse. Dispersiooni lahutusega osadeks kontrollitakse hüpoteesi, et vaadeldav mudel aja kaudu on statistiliselt sama kirjeldusjõuga nagu ainult konstanti sisaldav mudel (st keskmisega võrdumise mudel). Esitatakse sellekohane F-statistik ja olulisuse tõenäosus.
Tabeli 3 kolmandas osas kirjeldatakse trendijoone võrrandit:
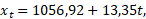
kus t on vaadeldava perioodi aasta järjekorranumber (või aasta, kui oleksime kasutanud aastanumbreid), t = 1, 2, …, 41.
Lineaarse mudeli kohaselt kasvab rahvaarv aasta keskmiselt 13.35 tuhande võrra. Lineaarse trendi kohane rahvaarv 1959. aastal on 1056,92 + 13,35 ∙ 10 = 1190,42 ja 1979. aastal 1056,92 + 13,35 ∙ 30 = 1457.42. Kui võrrelda neid tegeliku rahvaarvuga neil aastail, mis on vastavalt 1191.43 ja 1464.48, siis võiks öelda, et lineaarse prognoosi viga ei ole suur. Tabelis on esitatud veel ka standarditud andmeile vastav kordaja (võrdub üheainsa seletava tunnuse korral korrelatsioonikordajaga) ja t-statistik (kordaja ja selle standardhälbe suhe) kontrollimaks hüpoteesi kordaja võrdumisest nulliga, mille tulemuseks esitatakse olulisuse tõenäosus.
Tabel 3. 1950.–1990. aastate rahvaarvule lineaarse trendi sobitamine
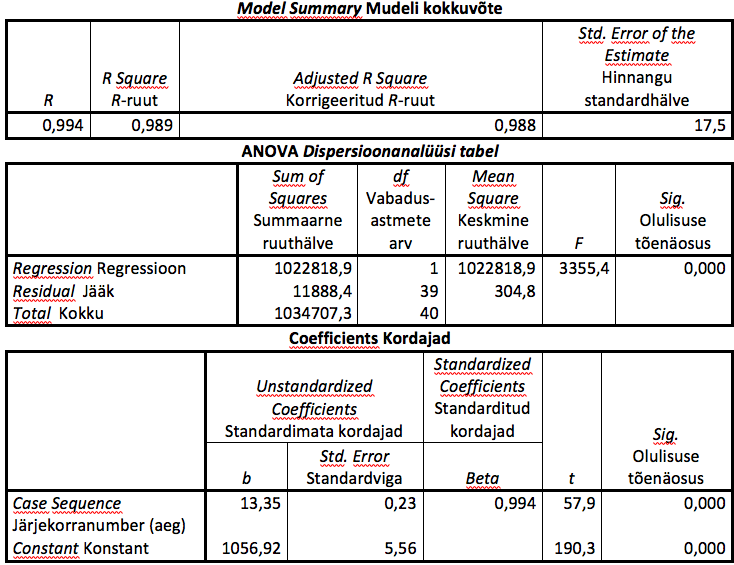
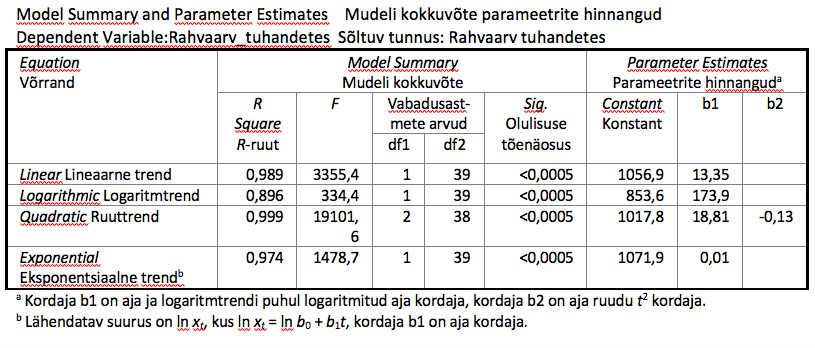
Katsetame ka teisi trendifunktsioone. Kui dispersioonanalüüsi detailset tabelit ei kasuta, siis tuuakse paketi SPSS korral mitut mudelit korraga sobitades esile kõigi kasutatud mudelite ühine kokkuvõte (tabel 4), milles esitatakse determinatsioonikordaja, tähtsamad osad dispersioonanalüüsi tabelist (vrd lineaarse trendi rida tabeli 3 keskmise osaga) ja trendi mudeli kordajad (vrd lineaarse mudeli rida tabeliga 3). Näeme, et ruuttrendi kirjeldusaste on suurim ja logaritmilise trendi kasutamine on suhteliselt ebaõnnestunum valik. Ruuttrendi võrrand on:
xt = 1017,77 + 18,81 t – 0,130 t2,
kus t = 1, 2, …, 41. Sellest nähtub, mida hilisem aasta, seda väiksem on rahvaarvu kasv aja seisukohalt (aja ruudu kordaja on miinusmärgiga, aja kordaja plussmärgiga). Vähenevat kasvutempot nägime ka jooniselt 4 ja nüüd ilmnes aeglustuv rahvaarvu kasv ka teist laadi analüüsi kaudu.
Tabel 4. Erinevate trendide sobitamine 1950.–1990. aastate rahvaarvule
 L
L
Logaritmilise trendi võrrand on:
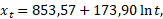
millest näeme taas aeglustuvat kasvu aja seisukohalt (logaritmteisendus „surub kokku“ suuremaid väärtusi, aga paraku intuitiivselt raskesti tajutavalt). Sobitamisel logaritmfunktsiooni kaudu ei liikunud mõte siiski väga vales suunas, sest saab lihtsalt näidata, et sel juhul aegrea juurdekasvutempo on pöördvõrdeline ajaga. Siiski osutus regressioonimeetodil leitud parim logaritmiline trendikõver kahanemises liiga järsuks. Seda näeme jooniselt 6, kus on kujutatud tabelis 4 kirjeldatud trendijooned tegeliku aegrea kõrval.
Eksponentsiaalse trendi leidmisel sobitatakse lähendjoont aegrea liikmete logaritmidest moodustatud aegreale, st ln xt = ln b0 + b1t. Näeme, et sobitusaste on determinatsioonikordaja alusel kõrge, aga lahknevus aegrea punktidest (viga, prognoosijääk) suurem kui lineaarse lähendi korral (joonis 6).
Ruuttrend järgib kõige täpsemalt aegrida. Selgelt on näha lineaarse trendi viga perioodi alguses ja lõpus ning keskel (nimetasime eespool joone kumerust). Eelnevalt toodud näide lineaarse trendi hea täpsuse kohta oli meelega valitud kohast, kus sirgjoon läbis vastavat punkti suhteliselt täpselt (10. ja 30. aasta) ja seepärast jäi mulje heast lähendist. Nüüd kummutasime selle pistelise mulje.
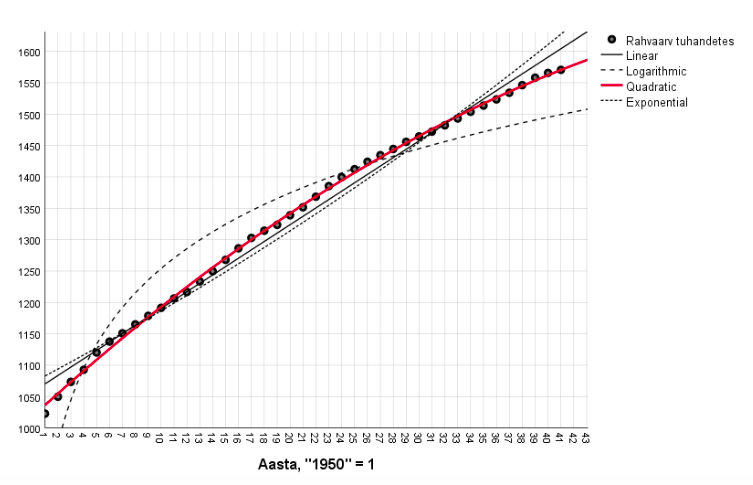
Tõlge: Linear – lineaarne funktsioon, Logarithmic – logaritmfunktsioon, Quadratic – ruutfunktsioon, Exponential – eksponentfunktsioon
Tabelis 5 on esile toodud trendi suhtes arvutatud jääkide (aegrea liige miinus väärtus trendijoonel, püstjoone pikkus punktist trendijooneni) statistika. Ruuttrendi viga jääb -13.5 ja 11.7 vahele ja on märgatavalt väiksem kui kahel ülejäänud mudelil. Vea keskmine on trendi konstruktsiooni kohaselt 0, aga standardhälbed varieeruvad tugevalt, nt ebaõnnestunult valitud logaritmtrendi puhul on see kümnekordne ruuttrendiga. Ka eksponentsiaalse trendi vigade standardhälve on suhteliselt suur.
Tabel 5. Erinevate trendide kohaste jääkide statistika

Kas trendi alusel võiks teha ka prognoose (ik forecast, prognosis, prediction)? Põhimõtteliselt jah, kuid väga piiraval eeldusel: juhul, kui aegrea trend oluliselt ei muutu. Kui seda on võimalik veenvalt tõendada, siis mida täpsemalt on määratud senine trend, seda parema prognoosi saame. Praktikas, eriti suurte keeruliste süsteemide korral nõuab ennustamine väga suurt ettevaatust ja on mõeldav vaid lähituleviku jaoks. Vaadelge selle üle järele mõeldes veel kord rahvaarvu joonist 2 ja kujutlege, kui hea ennustuse saaksime − käänupunkte kõrvale jättes – mõne formaalse trendijoone alusel, mis leitakse alates 1990. aastast kujunenud aegrea põhjal.
Aegrea sobitamine lähendfunktsiooniga tähendab aegrea asendamist selle ühe komponendiga, nimelt trendiga (koos sesoonsuse ja tsüklilisusega, kui need on olemas), jättes kõrvale juhusliku osa, juhusliku komponendi. Järgmises osas vaatleme sisuliselt sama ülesannet, millega äsja tegelesime, kuid lahendame seda teiselt poolt, juhusliku osa väljajätmise (vähendamise) teel.
Kuidas leida trendi aegreas paketi SPSS abil?Trendi mudeli leidmist võib oluliselt raskendada see, kui aegrea juhuslik komponent tuleb tugevalt esile ja aegrida on hüplik. Meenutage näiteks 1950.–1990. aastate kasvutempo aegrida (joonis 5). Seepärast võiks kõne alla tulla trendi leidmine ka alles pärast juhusliku osa eemaldamist aegreast. Aegrea juhusliku osa matemaatiline külg (statistiline jaotus jm) jääb siinkohal kõrvale ja kirjeldame allpool võimalusi juhusliku osa analüüsiks aegrea silumise ehk tasandamise teel (ik smoothing). Silutud aegreas on kergem märgata trendi ja on ilmekas esile tuua muidki aegrea omadusi (kasvutempo, juurdekasvud). Silumise järel võiks silutud aegrida trendi mudeli saamiseks lähendada mõne kõveraga ja üldse edasi analüüsida nagu mis tahes teist aegrida. Silumine tähendab uue, vähem variatiivse juhusliku komponendiga aegrea moodustamist. Silumismeetodeid on mitmeid ja siinkohal tutvustame neist kaht: libiseva keskmise (või libiseva mediaaniga) silumist ja aegrea eelnevatele olekutele toetuvat eksponentsiaalset silumist. Libiseva keskmise meetodil on praktikas mitmeid variatsioone, sh kaalutud keskmist kasutades. Tutvustame sagedasimat varianti, mida teades ei ole ka võimalikke modifikatsioone raske mõista.
Silumine tsentreeritud libiseva keskmise meetodil (ik central moving average method). Igas aegrea punktis (välja arvatud teatav arv esimesi ja viimaseid) leitakse meie poolt ette antud arvu naaberpunktide ja aegrea antud liikme keskmine. See väärtus võetakse silutud aegreas vaadeldavas punktis silutud aegrea väärtuseks. Väljavalitud ajalõiku nimetatakse ka aknaks ja selles olevate punktide arvu akna laiuseks (silumise sammuks). Aken libistatakse silumiseks liikmelt liikmele üle terve aegrea. Mida laiema aknaga siluda (st mida suurem arv naaberpunkte kaasata), seda siledam tuleb uus aegrida. Libisevat keskmist rakendatakse ka kaalutud keskmise vormis. Protseduur on lihtne siis, kui akna laius on paaritu arv ja „silutav“ aegrea liige asub akna keskel. Näiteks aknaga 3 libiseva keskmise meetodil silumisel on silutav (ülemine) ja silutud aegrida (alumine) järgmised (mõned sammuga 3 moodustatud akna asendid on toonitud):

Esialgse aegrea suurim ja vähim väärtus olid vastavalt 5 ja 1 (haare 4) ning silutud reas 4 ja 7/3=2,3 (haare 1.3), st hüplikkus tasandus. Paarituarvulise sammuga k siludes „lüheneb“ aegrida kummastki otsast (k-1)/2 liikme võrra (asendatakse andmelüngaga).
Esialgse aegrea suurim ja vähim väärtus olid vastavalt 5 ja 1 (haare 4) ning silutud reas 4 ja 7/3=2,3 (haare 1.3), st hüplikkus tasandus. Paarituarvulise sammuga k siludes „lüheneb“ aegrida kummastki otsast (k-1)/2 liikme võrra (asendatakse andmelüngaga).
Paarisarvulise laiusega k akna puhul ei ole üheselt selge, millisele liikmele aknas olevate liikmete keskmine omistada, see koht asub kahe liikme vahel. Kirjeldame näite abil protseduuri, kus sellisel juhul silutakse aegrida kaks korda: esmalt koostatakse aegrida, kus paarisarvulise laiusega k akna liikmete keskmine omistatakse akna keskmesse jäävate liikmete vahel olevale fiktiivsele liikmele, ja seejärel silutakse seda rida akna laiusega 2 (st leitakse naaberliikmete keskmine). Näiteks aknaga 4 libiseva keskmise meetodil silumisel on silutav ja silutud aegrida järgmised:

Saadud aegreas on märgatavalt väiksem hüplikkus võrreldes nii esialgse kui ka sammuga 3 silutud aegreaga. Paarisarvulise sammuga k siludes arvestatakse aegrea kummaski otsas k/2 aegrea liiget andmelüngaks.
Silumine eelnevate olekute libiseva keskmise meetodil (ik prior moving average method). Igas aegrea punktis (välja arvatud teatav arv esimesi) leitakse meie poolt ette antud arvu liikmete keskmine ja see arvestatakse silutud aegrea väärtuseks antud ajamomendil. Nii siludes rõhutatakse aegrea järjepidevust. Näiteks aknaga 3 eelnevate olekute libiseva keskmise meetodil silumisel on silutav ja silutud aegrida järgmised:

Aegrea esimesed k liiget arvestatakse andmelüngaks.
Silumine libiseva mediaani meetodil (ik moving median method). Meetod on sarnane tsentraalsele libiseva keskmise meetodile, kuid keskmise asemel leitakse mediaan. Paarisarvulise laiusega akna korral võib kasutusel olla erinevaid mediaani leidmise viise. Näiteks aknaga 3 libiseva mediaani meetodil silumisel on silutav ja silutud aegrida järgmised:

Libiseva mediaani meetodit sobib rakendada libiseva keskmise meetodi asemel siis, kui aegrida on tugevalt hüplik. Eksponentsilumine (exponential smoothing). Eksponentsilumise korral asendatakse aegrea liige xtuue väärtusega yt, milles on arvestatud kaaluga a praegust liiget ja kaaluga 1 – a eelmist juba silutud liiget:
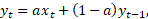
t = 1, 2, …, n, kus 0 < a < 1 ja y0 = x1. Mida väiksem on silumiskordaja a, seda siledam tuleb aegrida, sest aegrea esialgne väärtus omandab silutud väärtuses väikese kaalu ja eelmise ajamomendi juba silutud väärtus suurema. Suurust 1 – a nimetatakse ka sumbumisteguriks, sest see määrab, kuivõrd tasandub aegrea hüplik käik. Kui silumiskordaja on nullilähedane, siis on silutud aegrea liikmed ligikaudu võrdsed esialgse aegrea esimese liikmega. Kui silumiskordaja on arvu 1 lähedal, siis langeb silutud aegrida ligikaudu kokku esialgsega. Hüpliku rea puhul on kasulik valida väiksem ja suhteliselt tasase rea puhul suurem silumiskordaja.
Eksponentsilumisel arvestatakse iga liikme leidmisel järjest eelmisi ja lõppkokkuvõttes osutub silutud väärtus eelnevate liikmete kaalutud summaks (vt nt Sauga 2017, lk 567, või ka Vikipeedia artikkel Exponential smoothing). Kaalud moodustavad sumbumiskordaja geomeetrilise progressiooni, millest tulebki meetodi nimi. Mida kaugem on aegrea liige silutavast liikmest, seda kõrgemas astmes olev sumbumiskordaja on kaaluks, st seda väiksem mõju silutud väärtuse arvutamisel antud silumiskordaja korral (silumiskordaja on väiksem kui 1).
Eelnevalt kasutatud näite aegrida ja eksponentsilumisel saadav aegrida on silumiskordajate 0,4 (allpool teine rida) ja 0,8 (allpool kolmas rida) korral järgmised (sumbumiskordajad vastavalt 0,6 ja 0,2):

Selle silumisviisi korral aegrida silumisega ei „lühene“.
Kombineeritud silumismeetodid: loominguline erinevate meetodite järjestikune kasutus, mil silutud reale rakendatakse mõnd silumismeetodit uuesti. Üks sellekohane näide on paketi SPSS silumisprotseduur T4253H libiseva mediaani jm meetodite korduva rakendamise teel.
Tabelis 6 on esile toodud siinvaadeldud näite erinevate silumistulemuste kokkuvõte. Mida laiema aknaga libiseva keskmise meetodil siluda, seda lühemaks läheb silutud aegrida, kuid ühtlasi ka seda enam siledaks. Aknaga 4 silutud aegrea standardhälve on poole väiksem kui aknaga 3 silumise korral ja ka haare on väiksem. Ülejäänud aegridade puhul on standardhälve 0,5–0,6 ringis, seega mitu korda väiksem kui esialgses aegreas. Keskmine on vahemikus 3,0–3,2. Eksponentsilumisel on saavutatud suurema sumbumisfaktoriga siledam rida (väiksem standardhälve). Haare peegeldab hüplikkuse ulatust ja see on vähim sammu 4 korral ning suurim väikese sumbumisfaktoriga eksponentsilumisel.
Tabel 6. Erinevate silumisviiside näite kokkuvõte
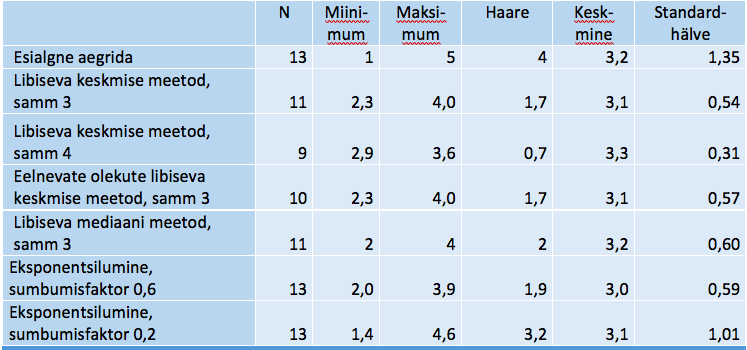
Paketi SPSS abil on võimalik rakendada kõiki siinkirjeldatud silumisviise, välja arvatud eksponentsilumine (vt tekstikasti „Aegridade silumine paketi SPSS abil“). MS Office Excel võimaldab nii libiseva keskmise meetodil kui ka eksponentmeetodil silumist (menüüst Data – Data Analysis ja sealt valida moodulid Exponential Smoothing ja Moving Average).
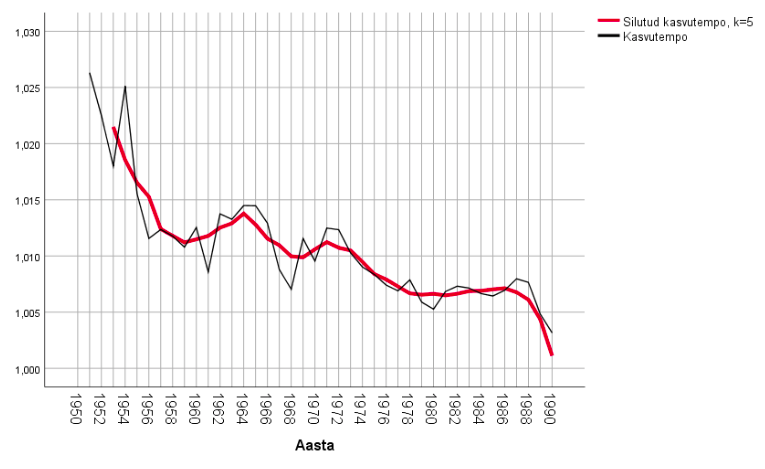
Pöördume tagasi rahvastikuarvu kasvu näite juurde. Joonisel 7 on näidatud 1950.–1990. aastate rahvaarvu kasvutempo (ahelindeksi) esialgne ja libiseva keskmise meetodil silutud aegrida (silumisakna laius 5). Näeme langevat trendi ja seejuures terve perioodi vältel. Rahvastikukasv aeglustus.
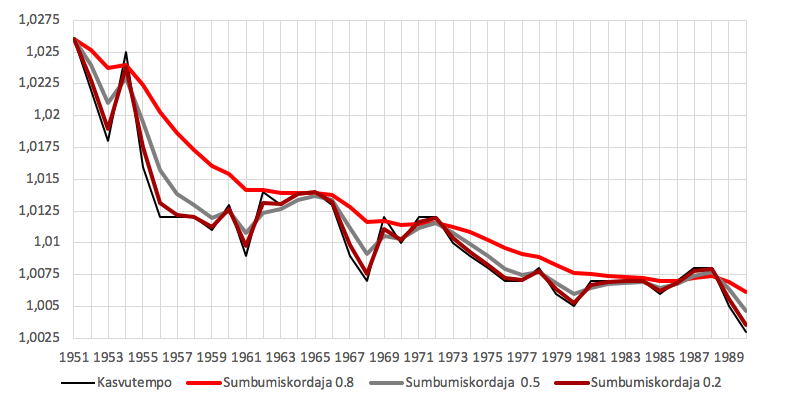
Joonisel 8 on kujutatud sama aegrea silumine eksponentmeetodil kolme eri sumbumiskordaja korral. Suurem sumbumiskordaja annab siledama aegrea, mis algusaastate suure kasvutempo tõttu lahkneb aegrea alguses üsnagi esialgsest aegreast. Siin oleks võinud esimest kümmet aastat käsitleda eraldi. Väike sumbumiskordaja aegrida suurt ei muuda. Võrdne osakaal – pool aegrea liikmest ja pool eelmisest silutud liikmest – tasandab suuremad hüpped, kuid järgib üsna hoolega aegrea käiku.
Kuidas prognoosida aegrea edasist kulgu silutud aegrea abil? Võiks kasutada viimase ajamomendi silutud väärtust. Aegrea käänupunktides ei tule ennustus täpne, aga vähese püsiva languse või tõusu puhul ei oleks vahel väga vigagi.
Aegridade silumine paketi SPSS abilVaatleme lõpuks aegrea perioodilise komponendi analüüsivõimalusi. Kui aegrea käik kordub teatud perioodiga, siis on võimalik analüüsi üles ehitada mitmel viisil, kasutades trendi eemaldamise ja aegrea silumise ning perioodilisuse eemaldamise protseduure erinevas järjekorras. Üks võimalus oleks selgitada välja trend ja edasi analüüsida trendivaba rida, millest eemaldada veel ka sesoonsus. Kui järele jääb juhuslik komponent, mille trendijooneks on nulltase, siis olemegi aegrea osad identifitseerinud. Tsüklilisuse uurimise jaoks (suured ebakorrapärased perioodid) läheb tavaliselt aegreale lisaks vaja kontekstuaalset teavet keskkonna kohta, milles aegrida mõõdeti (nt süsteemi sotsiaalne taust).
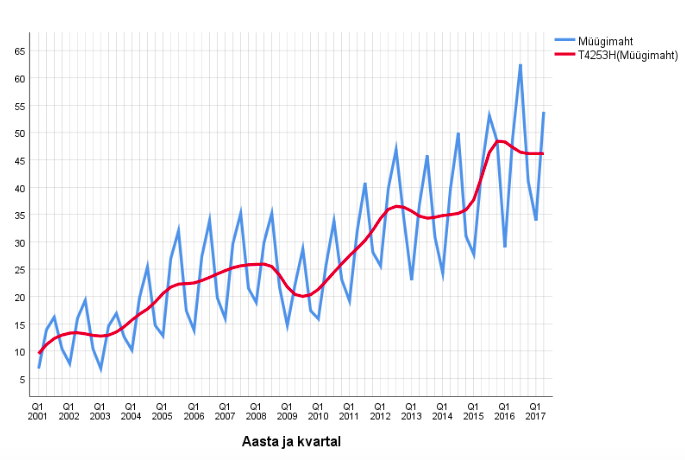
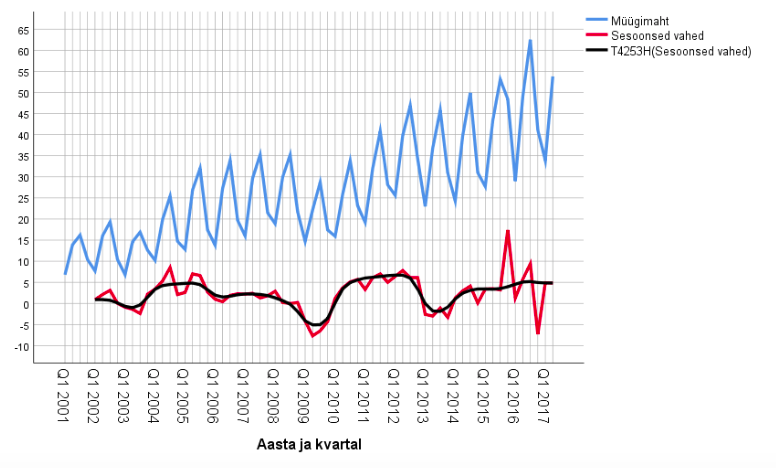
Joonisel 9 on kujutatud ilmset sesoonsust peegeldav aegrida, milles perioodilisus peitub mõõdetud suuruse olemuses. Majutusasutuste tegevus on Eestis klimaatiliselt sesoonne ja jooniselt peegeldub majutusteenuse selge perioodiline kulg aastase perioodiga. Müügi tipp on kolmas kvartal ja põhi esimene kvartal. Lisaks on joonisele kantud aegrea komplekssel silumisel saadud trendijoon, mis viitab lineaarse trendi küllalt heale sobivusele selle aegrea kirjeldamisel (suurem väljalöök sellest 2009–2010. aastate paiku ja 2013–2014. aastate paiku).
Kui kas protsessi sisu või näiteks aegrea joonise alusel on põhjust oletada sesoonsust, siis tähendab see seda, et teatud sammuga peaksid aegrea liikmed olema korreleeritud, st perioodi piires sama ajalise paigutusega liikmed peaksid olema positiivselt korreleeritud. See mõte on realiseeritud aegrea autokorrelatsioonifunktsiooni (ik autocorrelation function, ACF) kaudu, mil aegrida korreleeritakse sama aegrea nihutatud variandiga ühe, kahe, kolme jne ajamomendi võrra. Ajanihet nimetatakse viitajaks (ik lag ja lead, vastavalt sellele, kas aegrida nihutatakse hilisemaks või varasemaks). Kui perioodi vastavad „sakid“ sattuvad nihutades kohakuti (see juhtub iga perioodi pikkusega võrduva viitaja korral), siis peaks korrelatsioon tulema tugevam kui ülejäänud juhtudel. Autokorrelatsioonifunktsiooni suuremad väärtused viitavad perioodi pikkusele.
Mida tähendab viitajaga nihutamine? Selgitame seda järgneva skeemiga kvartalite nihutamise kohta kuni viitajaga 5. Negatiivse viitaja korral nihutatakse aegrida vastupidises suunas, varasemaks. Viitajaga 1 liigub esimene kvartal kohakuti sama aasta teise kvartaliga, viitajaga 2 kolmanda kvartaliga, viitajaga 3 neljanda kvartaliga ja viitajaga 4 järgmise aasta esimese kvartaliga.
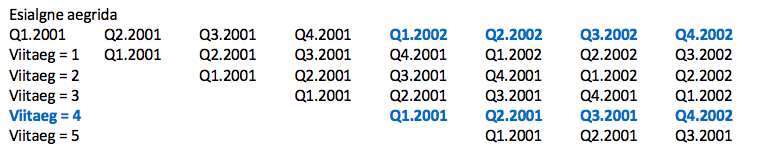
Autokorrelatsioon on aegrea korrelatsioon iseendaga ja kõneleb sellest, kuivõrd aegrida “mäletab” eelnevaid olekuid, st kui pikalt aja kulgedes oleneb aegrea väärtus sellest, mis oli varem. Viitaja maksimumi valik on enda teha ja seda valides võiks kaaluda protsessi sisu arvestades, kui pikk võiks olla see „mälu“.
Autokorrelatsioonifunktsiooni arvutuseeskiri on analoogiline üldtuntud korrelatsioonikordaja eeskirjale: viitaja k, k =1, 2, … korral
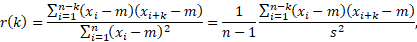
kus m on aegrea keskmine ja s standardhälve. Kui aegreas esineb trend, võiks selle autokorrelatsiooni sisuka tõlgenduse saamiseks aegreast eelnevalt eemaldada (st vaadelda jääkaegrida, kui igast liikmest lahutada trendikohane väärtus). Aegrea autokorrelatsioonide diagrammi kohta kasutatakse ka mõistet korrelogramm.
Siinkohal on sobiv juhus nimetada aegridade esmasanalüüsis mõnikord kasulikku teist korrelatsioonanalüüsi rakendust, nimelt kahe (või ka enama) eri aegrea vahelist korrelatsioonseost, mille iseloomustamiseks arvutatakse viitaja suhtes ristkorrelatsioonifunktsiooni väärtused (ik cross correlation function, CCF). Kahe aegrea vaheline (rist)korrelatsioon on samuti “tavalise” korrelatsioonikordaja analoog. Aegridade ristkorrelatsioon võib kergesti osutuda pseudokorrelatsiooniks, mistõttu kasutada seda ettevaatlikult (vt nt Dean ja Dunsmuir 2016).
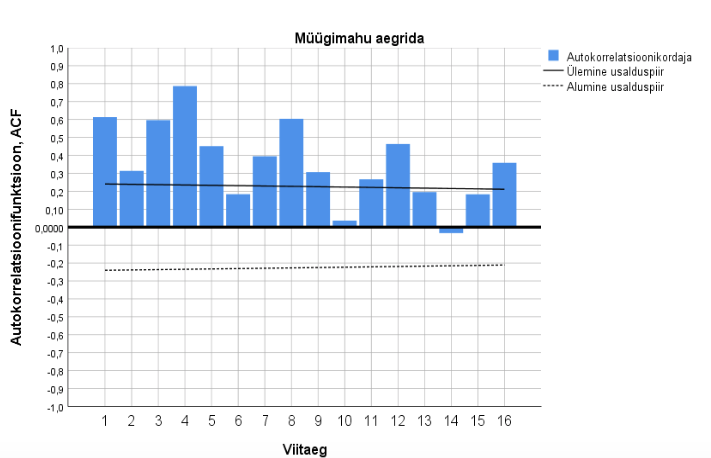
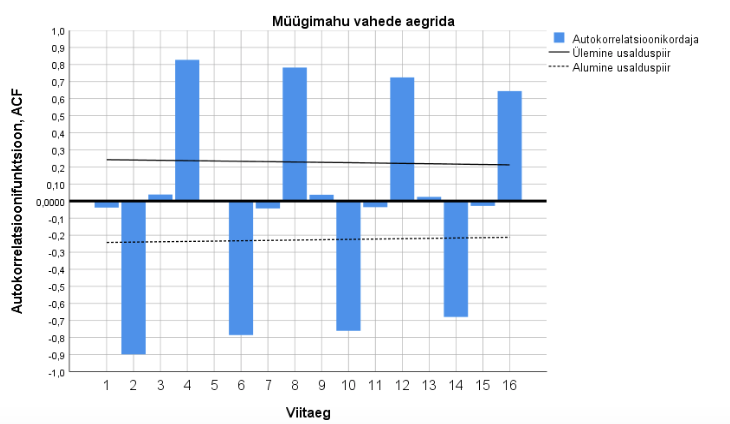
Jätkame müügimahu näidet ja toome esile müügimahu autokorrelatsioonifunktsiooni väärtused viitaja maksimumi 16 korral, kasutades paketi SPSS tulemusi. Joonisel 10 on esitatud korrelogramm kuni viitajaga 16 ja sellel näeme selgelt tugevamaid korrelatsioonikordajaid viitaja muutudes perioodiga 4 kvartalit. Autokorrelatsioon tuhmub nelja perioodi (aasta) jooksul tunduvalt: väärtusest 0,8 väärtuseks alla 0,4. Kasvava trendi tõttu (joonis 9) on ka perioodi seisukohalt kohakuti mittesattunud kvartalite müügimahtude vahel statistilisi seoseid ja selgema pildi huvides arvutame autokorrelatsioonifunktsiooni veel ka müügimahtude aegreas, kui sellest on eemaldatud lineaarne trend, st leitud vahede rida, absoluutsed juurdekasvud. Joonis 10, kus paikneb vastav korrelogramm (alumine), näitab perioodilisust ilmekamalt. „Otse vastupidiste“ kvartalite 1 ja 3 juurdekasvud on kohakuti sattudes tugevalt negatiivselt korreleeritud.
Niisiis on nii sisuliselt kui ka statistiliselt tõendatud, et vaadeldavas aegreas esineb aastapikkune sesoonsus. Et ligikaudu sobib ka lineaarne trend, siis kõrvaldame nüüd selle sesoonsete vahede aegrea moodustamise teel ja seejärel peaksime tulemuseks saama ainult juhuslikku komponenti sisaldava aegrea. Üks asjaolu jääb seejuures siiski arvestamata, nimelt see, et perioodilisuse amplituud aja jooksul ei ole püsiv, vaid pigem kasvab, ja see peaks peegelduma jääkrea lõpu suuremas dispersioonis võrreldes algusega. Joonisel 11 on kujutatud esialgne aegrida, sesoonsete vahede rida ja sesoonsete vahede rida kompleksselt silutud kujul. Sesoonsete vahede reas on raske mingit suundumust märgata (analüüs näitas, et eri liiki trendijoonte sobitamine annab ainult paariprotsendilise kirjeldusastme). Seega võiks meie lõppjäreldus olla: müügimahud on sesoonselt lineaarse trendiga. Prognoos järgnevaks aastaks tuleks seejuures teha kvartalite kaupa. Sellise lähenduse viga on perioodi lõpuaastail pisut suurem kui alguses.
Bollwerk, B. (2001). Aegridade analüüs statistikapaketis SPSS. Tallinn: TLÜ. (http://www.cs.tlu.ee/~katrin/wp/wp-content/uploads/2013/11/algread.pdf; vaadatud 22.12.2019).
Curve Estimation Models. IBM Knowledge Center. (https://www.ibm.com/support/knowledgecenter/SSLVMB_sub/statistics_mainhelp_ddita/spss/base/curve_estimation_models.html; vaadatud 22.12.2019).
Dean, R.T., Dunsmuir, W.T.M. (2016). Dangers and uses of cross-correlation in analyzing time series in perception, performance, movement, and neuroscience: The importance of constructing transfer function autoregressive models. Behaviour Research 48, 783–802.
Eesti sotsiaaluuring. (https://www.stat.ee/eesti-sotsiaaluuring; vaadatud 22.12.2019).
Eesti Statistikaamet. Terminite sõnastik. (https://www.stat.ee/76870#a; vaadatud 22.12.2019)..
e-Handbook of Statistical Methods, NIST/SEMATECH. (http://www.itl.nist.gov/div898/handbook/, https://www.itl.nist.gov/div898/handbook/pmc/section4/pmc4.htm; vaadatud 30.12.2019).
European Social Survey. Data and Documentation. (https://www.europeansocialsurvey.org/data/; vaadatud 30.12.2019).
Harro, J., Kiive, E., Orav, P., Veidebaum, T. (toim). (2015). Lapsest täiskasvanuks, Eestis. ELIKTU 1998-2015. Tartu: Eesti Ülikoolide Kirjastus.
Kangro, R. (2016). Aegridade analüüs. (https://courses.ms.ut.ee/MTMS.01.023/2016_fall/uploads/Main/aegread.pdf; vaadatud 22.12.2019).
Kenkmann, P., Saarniit, J. (toim). (1998). Longituuduurimused: kogemusi ja tulemusi. Tartu: Tartu Ülikooli Kirjastus.
Paas, T. (1995). Sissejuhatus ökonomeetriasse. Tartu: Tartu Ülikooli Kirjastus.
Sauga, A. Interaktiivsed demod statistikas ja ökonomeetrias. Wolfram-keskkond. (https://www.sauga.pri.ee/cdf/; vaadatud 22.12.2019).
Sauga, A. (2017). Statistika õpik majanduseriala üliõpilastele. Tallinn: TTÜ Kirjastus. (https://www.digar.ee/viewer/et/nlib-digar:312875/273207/page/548; vaadatud 22.12.2019).
STAT 510. Applied Time Series Analysis. The Pennsylvania State University. (https://onlinecourses.science.psu.edu/stat510/lesson/1; vaadatud 22.12.2019).
Titma, M. (toim). (1999). Kolmekümneaastaste põlvkonna sotsiaalne portree. Tartu-Tallinn: Teaduste Akadeemia Kirjastus.
Titma, M. (toim). (2002). 30- ja 50-aastaste põlvkonnad uue aastatuhande künnisel. Tartu: Tartu Ülikooli Kirjastuse trükikoda.
Tooding, L.-M. (2015). Andmete analüüs ja tõlgendamine sotsiaalteadustes. Tartu: Tartu Ülikooli Kirjastus, p 1.2.2–1.2.4.
Tuma, N. B. (2004). Modeling change. Melissa Hardy ja Alan Bryman (toim.), Handbook of data analysis, (lk 309–330). London: Sage Publications.
|
Eesti rahvaarv seisuga 1. jaanuar. Allikas: Eesti statistika andmebaas, RV021, 22.12.2019 | |||||
|
Aasta |
Rahvaarv |
Aasta |
Rahvaarv |
Aasta |
Rahvaarv |
|
1919 |
1069344 |
1955 |
1137640 |
1991 |
1567749 |
|
1920 |
1059000 |
1956 |
1150791 |
1992 |
1554878 |
|
1921 |
1076543 |
1957 |
1165009 |
1993 |
1511303 |
|
1922 |
1097733 |
1958 |
1178717 |
1994 |
1476952 |
|
1923 |
1107130 |
1959 |
1191428 |
1995 |
1448075 |
|
1924 |
1114498 |
1960 |
1206362 |
1996 |
1425192 |
|
1925 |
1116730 |
1961 |
1216712 |
1997 |
1405996 |
|
1926 |
1117270 |
1962 |
1233441 |
1998 |
1393074 |
|
1927 |
1116343 |
1963 |
1249804 |
1999 |
1379237 |
|
1928 |
1114941 |
1964 |
1267910 |
2000 |
1401250 |
|
1929 |
1116553 |
1965 |
1286262 |
2001 |
1392720 |
|
1930 |
1114748 |
1966 |
1302870 |
2002 |
1383510 |
|
1931 |
1117445 |
1967 |
1314323 |
2003 |
1375190 |
|
1932 |
1119339 |
1968 |
1323569 |
2004 |
1366250 |
|
1933 |
1123734 |
1969 |
1338858 |
2005 |
1358850 |
|
1934 |
1124769 |
1970 |
1351640 |
2006 |
1350700 |
|
1935 |
1127928 |
1971 |
1368511 |
2007 |
1342920 |
|
1936 |
1129804 |
1972 |
1385399 |
2008 |
1338440 |
|
1937 |
1130143 |
1973 |
1399637 |
2009 |
1335740 |
|
1938 |
1131161 |
1974 |
1412265 |
2010 |
1333290 |
|
1939 |
1133917 |
1975 |
1424073 |
2011 |
1329660 |
|
1940 |
1121939 |
1976 |
1434630 |
2012 |
1325217 |
|
1941 |
1977 |
1444522 |
2013 |
1320174 | |
|
1942 |
1978 |
1455900 |
2014 |
1315819 | |
|
1943 |
1979 |
1464476 |
2015 |
1313271 | |
|
1944 |
1980 |
1472190 |
2016 |
1315944 | |
|
1945 |
1981 |
1482247 |
2017 |
1315635 | |
|
1946 |
1982 |
1493085 |
2018 |
1319133 | |
|
1947 |
1983 |
1503743 |
2019 |
1324820 | |
|
1948 |
1984 |
1513747 |
2020 |
1328360 | |
|
1949 |
1985 |
1523486 | |||
|
1950 |
1022906 |
1986 |
1534076 | ||
|
1951 |
1049831 |
1987 |
1546304 | ||
|
1952 |
1073439 |
1988 |
1558137 | ||
|
1953 |
1092763 |
1989 |
1565662 | ||
|
1954 |
1120213 |
1990 |
1570599 | ||
|
Majutusasutuste müügimaht, miljonit eurot. Allikas: Eesti statistika andmebaas, tabel TU121, 28.12.2017 | |||||
|
Aasta |
Kvartal |
Müügimaht, miljonit eurot |
Aasta |
Kvartal |
Müügimaht, miljonit eurot |
|
2001 |
1 |
6.8 |
2010 |
1 |
15.9 |
|
2001 |
2 |
13.9 |
2010 |
2 |
25.9 |
|
2001 |
3 |
16.2 |
2010 |
3 |
33.8 |
|
2001 |
4 |
10.4 |
2010 |
4 |
23.1 |
|
2002 |
1 |
7.7 |
2011 |
1 |
19.2 |
|
2002 |
2 |
16 |
2011 |
2 |
32 |
|
2002 |
3 |
19.3 |
2011 |
3 |
40.8 |
|
2002 |
4 |
10.4 |
2011 |
4 |
28.1 |
|
2003 |
1 |
6.8 |
2012 |
1 |
25.6 |
|
2003 |
2 |
14.6 |
2012 |
2 |
39.8 |
|
2003 |
3 |
16.9 |
2012 |
3 |
46.9 |
|
2003 |
4 |
12.6 |
2012 |
4 |
34.2 |
|
2004 |
1 |
10.2 |
2013 |
1 |
23 |
|
2004 |
2 |
19.9 |
2013 |
2 |
36.8 |
|
2004 |
3 |
25.4 |
2013 |
3 |
45.8 |
|
2004 |
4 |
14.7 |
2013 |
4 |
30.9 |
|
2005 |
1 |
12.8 |
2014 |
1 |
24.3 |
|
2005 |
2 |
26.9 |
2014 |
2 |
39.8 |
|
2005 |
3 |
32 |
2014 |
3 |
49.9 |
|
2005 |
4 |
17.4 |
2014 |
4 |
31 |
|
2006 |
1 |
13.8 |
2015 |
1 |
27.7 |
|
2006 |
2 |
27.3 |
2015 |
2 |
43.3 |
|
2006 |
3 |
33.9 |
2015 |
3 |
53.1 |
|
2006 |
4 |
19.7 |
2015 |
4 |
48.4 |
|
2007 |
1 |
16 |
2016 |
1 |
29 |
|
2007 |
2 |
29.7 |
2016 |
2 |
49 |
|
2007 |
3 |
35.2 |
2016 |
3 |
62.5 |
|
2007 |
4 |
21.5 |
2016 |
4 |
41.1 |
|
2008 |
1 |
18.9 |
2017 |
1 |
33.9 |
|
2008 |
2 |
29.9 |
2017 |
2 |
53.8 |
|
2008 |
3 |
35.2 | |||
|
2008 |
4 |
21.7 | |||
|
2009 |
1 |
14.7 | |||
|
2009 |
2 |
22.2 | |||
|
2009 |
3 |
28.7 | |||
|
2009 |
4 |
17.4 | |||
Valminud Hariduse Infotehnoloogia Sihtasutuse IT Akadeemia programmi toel.


