Sotsiaalse Analüüsi Meetodite ja Metodoloogia õpibaas
T-test
Kadri Rootalu
2014
T-test
T-testi kasutatakse juhul, kui on vaja võrrelda kahe arvulise tunnuse keskmisi väärtusi või kahe grupi (nt meeste ja naiste) ühe arvulise tunnuse keskmisi väärtusi. T-test põhineb t-statistikul, mille väärtus arvutatakse välja, kasutades gruppide keskmisi ja standardhälbeid ning võttes arvesse ka vastajate arvu grupis (vt valemit). T-statistiku väärtused võivad olla nii positiivsed kui ka negatiivsed. T-statistiku absoluutväärtus on suur, kui gruppide keskmiste erinevus on suur.
T-statistiku väärtused on t-jaotusega. Suure vastajate arvu puhul tähendab see, et kahe grupi keskmiste erinevust näitavad juba t-statistiku väärtused, mis on absoluutväärtuselt suuremad kui 2 või 3. Väärtused 0 lähedal viitavad sellele, et gruppide keskmised on olnud väga sarnased.
Probleemid
- T-testi saab kasutada arvuliste tunnuste puhul, mis on ligilähedaselt normaaljaotusega.
- T-testi ei ole hea kasutada rohkem kui kahe grupi võrdlemiseks.
T-testi on võimalik teha kõigi levinumate statistikaprogrammidega (SPSS, STATA, EXCEL jms). Internetist võib leida ka kalkulaatoreid, mille abiga saab t-statistiku väärtuse välja arvutada olemasolevate keskmiste, standardhälvete ja vastajate arvude põhjal. Vt näiteks siit, siit ja siit.
Avage andmestik ess12eesti.sav
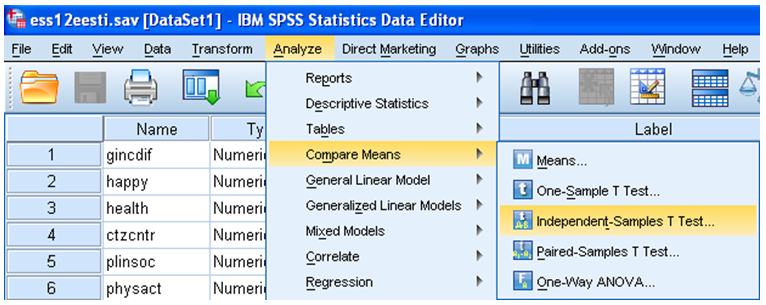
T-teste on võimalik teha mitme erineva ülesandepüstituse puhul. SPSSi analüüsimenüüst leiab T-testid alajaotusest „Compare Means“ ehk keskmiste võrdlus (joonis 1). Enim on kasutusel T-test kahe sõltumatu grupi võrdlemiseks (nt meeste ja naiste, kahe riigi vms keskmiste võrdlus) (joonis 2).
Analyze – Compare Means – Independent-Samples T Test
Joonis 1. T-testi tellimise menüü
Joonis 2. T-testi tellimise aken kahe sõltumatu grupi näitel
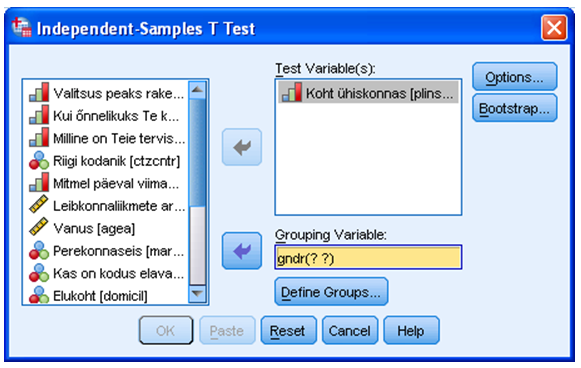
Näiteks soovime teada, kas mehed ja naised hindavad oma kohta ühiskonnas keskmiselt erinevalt. Selleks teeme tellimisaknas (joonis 2) järgmised valikud.
„Test Variable(s)“: sõltuv tunnus (see, mille keskmist tahame saada), neid võib olla ka mitu. See tunnus peab olema kindlasti arvuline. Praeguses näites on see „Koht ühiskonnas“.
„Grouping Variable“: grupeeriv tunnus. Sellel tunnusel peaksid olema eristatavad kaks gruppi. Neid gruppe võib tunnuse kategooriate hulgas olla ka rohkem, kuid võrrelda saab korraga vaid kahte. Praeguses näites valime sinna tunnuse „Sugu“.
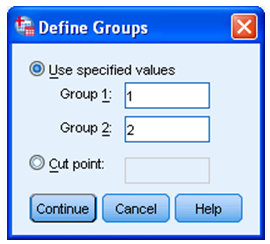
„Define Groups“: Selles alajaotuses tuleb määrata kahe võrreldava grupi koodid andmestikus (joonis 3). Soo tunnuse puhul on koodideks 1 ja 2 (need tuleb tunnuse kirjeldusest enne järele vaadata, nt klõpsates hiire parema klahviga tunnuse nimel).
Joonis 3. 1 ja 2 lahtrites määravad selles andmestikus meeste ja naiste koodi
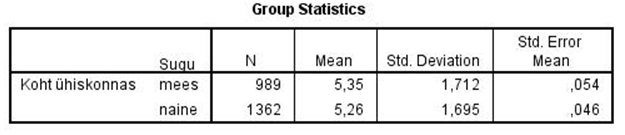
Väljund tulemustega esitatakse kahe tabelina. Esimeses neist (tabel 1) antakse kirjeldav statistika sõltuva tunnuse kohta gruppides.
Sealt võib näha, et meeste hinnang enda kohale ühiskonnas on keskmiselt 5,35 punkti ning naistel 5,26 punkti. Samuti esitatakse vastajate arv („N“), standardhälve („Std. Deviation“) ja keskmise standardviga („Std. Error Mean“) [vajadusel vaata täpsemalt kirjeldava statistika peatükist].
Tabel 1. Kirjeldav statistika gruppide kohta
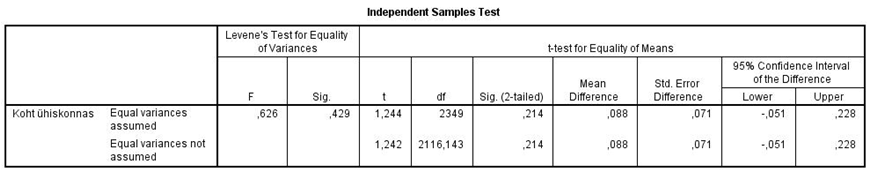
Teises tabelis (tabel 2) antakse t-statistiku ja gruppide võrdlusega seonduv.
Esimene osa tabelist „Levene’s Test …“ aitab meil otsustada, kumba tabeli rida kasutada. Kui selle testi tulemusena selgub, et tunnuse hajuvused gruppides ei ole erinevad (nagu praeguses näites), siis tuleks kasutada esimest tabeli rida. Kui erinevus on statistiliselt oluline (Sig teises veerus), siis tuleks kasutada tabeli teist rida.
T-statistiku väärtuseks meie näites on 1,244, vabadusastmete arv on 2349 ning olulisuse tõenäosus 0,214. Seega ei saa väita, et meeste ja naiste hinnangud enda kohale ühiskonnas keskmiselt üksteisest erineksid.
Tabelis 2 esitatakse ka keskmiste erinevus („Mean Difference“), selle standardviga ja usalduspiirid.
Tabel 2. T-statistik ja sellega seonduvad näitajad
Tooding, L.-M. (2007). Andmete analüüs ja tõlgendamine sotsiaalteadustes. Tartu: Tartu Ülikooli Kirjastus.
Märksõnad: t-statistik, t-test, keskmiste võrdlus
