
Sotsiaalse Analüüsi Meetodite ja Metodoloogia õpibaas
Korrelatsioonikordajad
Kadri Rootalu
2014
Korrelatsioonikordajaid kasutatakse seose uurimiseks kahe arvulise või pikema skaalaga järjestustunnuse vahel. Meetodi plussiks on, et see võimaldab kirjeldada nii seose suunda kui ka seose tugevust. Kõige sagedamini kasutatakse lineaarset ehk Pearsoni korrelatsioonikordajat ja Spearmani astakkorrelatsioonikordajat.
Lineaarne ehk Pearsoni korrelatsioonikordaja mõõdab lineaarset (ehk sirgjoonega kokkuvõetavat) seost kahe arvulise tunnuse vahel (vt valemit). Kui kahe tunnuse vahel koostatud hajuvusdiagrammi peal asuv punktiparv on sirgjoonega hästi kokkuvõetav, on korrelatsioonikordaja absoluutväärtus kõrge (vt nt joonis 1).
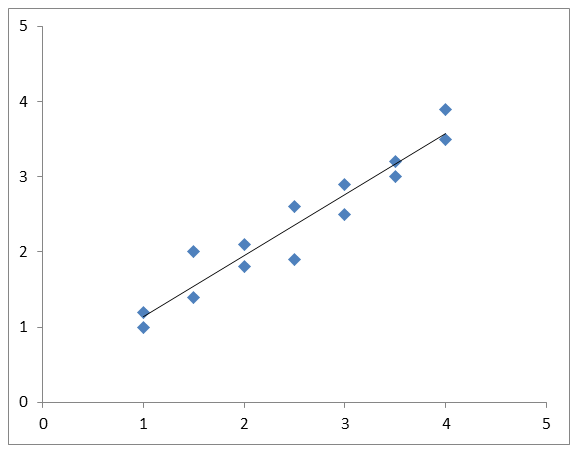
Korrelatsioonikordaja väärtused asuvad vahemikus -1 ja 1 vahel. Kui korrelatsioonikordaja väärtus on positiivne, siis tähendab see kasvavat seost tunnuste vahel: kui ühe tunnuse väärtus on suur, siis on tavaliselt suur väärtus ka teisel tunnusel. Näiteks inimese pikema kasvuga käib tavaliselt kaasas ka suurem kaal. Kui korrelatsioonikordaja väärtus on negatiivne, siis tähendab see kahanevat seost tunnuste vahel: ühe tunnuse suure väärtusega käib siis enamasti kaasas teise tunnuse väike väärtus. Näiteks inimese suurema sportimisele kulutatud tundide arvuga käib tavaliselt kaasas väiksem kaal. Kui korrelatsioonikordaja on 0, siis tunnuste vahel lineaarset seost ei ole, küll aga võib esineda mõnda muud tüüpi seos.
Arvamused selle kohta, kui suur peaks korrelatsioonikordaja olema, et seda tugevaks pidada, on sotsiaalteadustes ja reaalteadustes erinevad. Sotsiaalteaduste puhul võib küllaltki tugevaks seoseks pidada juba korrelatsioonseoseid tugevusega (absoluutväärtuselt) üle 0,5. Reaalteadustes on tugeva seose piir kaugemal.
Lineaarse korrelatsioonikordaja kasutamise probleemid
- Lineaarne korrelatsioonikordaja on tundlik erindite suhtes. Kui andmestikus on mõni indiviid, kelle tunnuse väärtused on teistest indiviididest väga palju erinevad, võib see korrelatsioonikordaja väärtust tugevalt mõjutada. See võib nt juhtuda siis, kui vastajate seas on mõni ülejäänutest tunduvalt suurema sissetulekuga või palju pikem või lühem vastaja.
- Lineaarne korrelatsioonikordaja annab infot ainult lineaarse seose kohta, muu kujuga seoste kohta mitte.
- Kui vastajate seas on mitu väga erinevat alamgruppi, siis lineaarse korrelatsioonikordaja kasutamine gruppideüleselt ei anna infot tegeliku seose suuna ja tugevuse kohta.
Mõned netimängud korrelatsioonanalüüsi teemal:
Rossman/Chance Applet Collection
http://www.rossmanchance.com/applets/GuessCorrelation.html
http://www.rossmanchance.com/applets/guesscorrelation/GuessCorrelation.html
Spearmani korrelatsioonikordajaga saab mõõta seost kahe arvulise või pikema skaalaga järjestustunnuse vahel. See sarnaneb lineaarse korrelatsioonikordajaga, kuid väljaarvutamisel kasutatakse tunnuse toorväärtuste asemel astakuid (ehk vastaja järjekorranumbreid tunnuse väärtuste järjestatud reas, vt valemit). Spearmani astakkorrelatsioonikordajat võiks nt kasutada, uurides seost järjestusskaalal mõõdetud usaldus- või meeldivushinnangute vahel, kuid kasutada võib ka arvulisi tunnuseid.
Avage andmestik ess12eesti.sav
Korrelatsioonanalüüsi tellimine paketis SPSS on võimalik omaette menüüjaotuse kaudu (vt joonis 1).
Analyze – Correlate – Bivariate
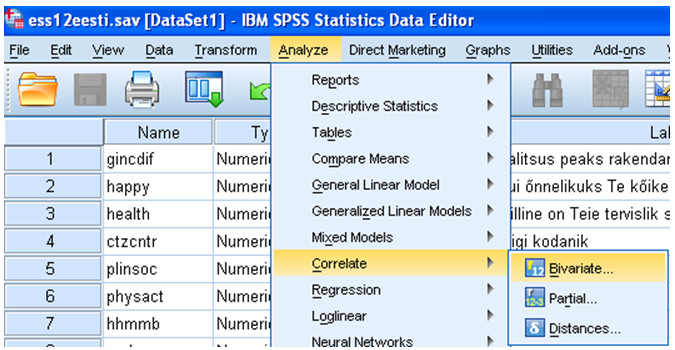
Aknasse „Variables“ (joonis 2) saata korrelatsioonimaatriksisse soovitavate tunnuste nimekiri. Tunnuseid peab olema vähemalt kaks, kuid võib olla ka rohkem.
Praeguses näites soovime teada, kuidas inimese hinnang enda kohale ühiskonnas on seotud tema õnnelikkuse ja haridusega. Selleks tuleks valida tunnused „Koht ühiskonnas“, „Kui õnnelikuks Te kõike kokkuvõttes end peate“ ja „Haridusaastate arv“. Tegemist on arvuliste tunnustega, seega saab nende puhul kasutada nii lineaarset korrelatsioonanalüüsi kui ka astakkorrelatsioonikordajaid.
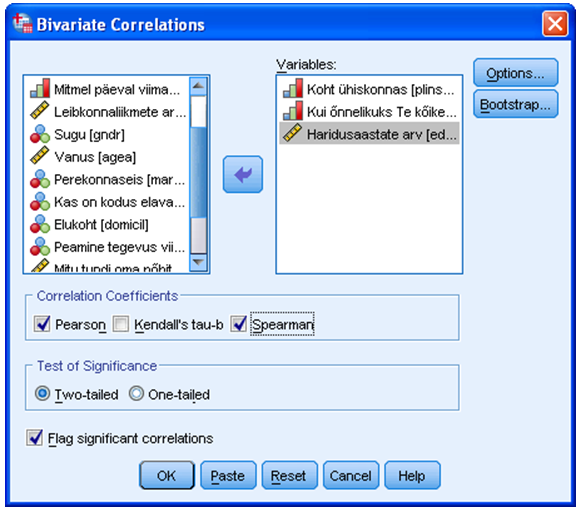
Tunnuste akna all (joonis 2) on võimalik valida korrelatsioonikordajat (vaikimisi Pearsoni ehk lineaarne korrelatsioonikordaja), lisaks ka Kendalli tau-b (veel üks astakkorrelatsioonikordaja) ja Spearmani korrelatsioonikordaja.
Valime Pearsoni ja Spearmani korrelatsioonikordajad. Tulemused esitatakse kahe tabelina, esimene (tabel 1) lineaarse (Pearsoni) ja teine (tabel 2) Spearmani korrelatsioonikordajate jaoks.
Tabel 1. Tulemused korrelatsioonimaatriksis, kasutades lineaarset korrelatsioonikordajat
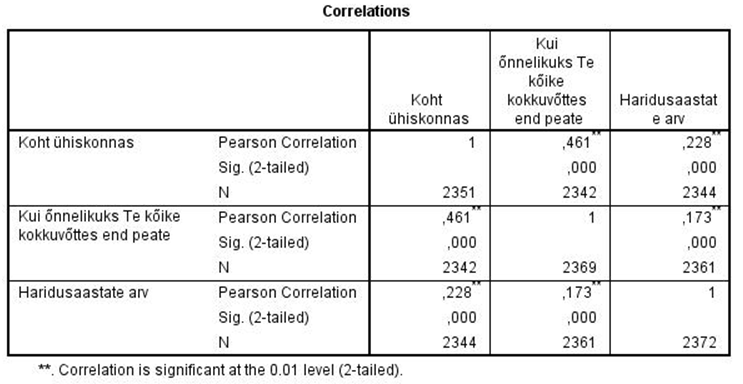
Väljundtabelis esitatakse lahtrites korrelatsioonikordaja, olulisuse tõenäosus ja vastajate arv. Iga tunnuspaari puhul võeti arvesse vaid neid vastajaid, kes olid vastanud mõlemale huvipakkuvale küsimusele. Sellest tulenevad ka erinevad vastajate arvud tabeli lahtrites. Esitatud korrelatsioonimaatriksi diagonaalis on väärtused 1 (tunnuse seos iseendaga) ning diagonaalist üles- ja allapoole jäävad kolmnurgad on üksteise peegeldused.
Vaadates seost õnnelikkuse ja ühiskondliku positsiooni vahel, võime öelda, et korrelatsioonikordaja väärtuseks on 0,461. See tähendab tugevapoolsemat positiivset seost: mida kõrgem on inimese hinnangul tema koht ühiskonnas, seda õnnelikum ta on. Tegemist on statistiliselt olulise seosega (olulisuse tõenäosus 0,000), mis on arvutatud välja 2342 vastaja vastuste põhjal.
Positiivsed on ka seosed hariduse ja õnnelikkuse (korrelatsioonikordaja 0,173) ning hariduse ja enda ühiskondliku positsiooni vahel (korrelatsioonikordaja 0,228).
Spearmani korrelatsioonikordajate väärtused erinevad pisut lineaarse korrelatsioonikordaja väärtustest, kuid ka seal on kõikide tunnuste vahel positiivsed seosed. See, kumb korrelatsioonikordajatest valida (kas lineaarne või Spearmani), sõltub konkreetse uurija uurimisülesandest.
Tabel 2. Tulemused korrelatsioonimaatriksis, kasutades Spearmani astakkorrelatsioonikordajat
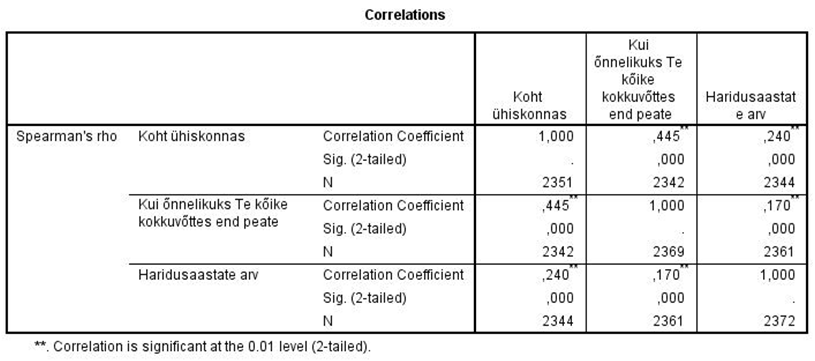
Avage andmestik ess12eestiexcel.xls
Korrelatsioonanalüüsi tellimiseks Excelis saab kasutada andmeanalüüsi moodulit „Data Analysis“. Selle alt tuleks valida menüü „Correlation“ (vt pilt 1).
Andmeanalüüsi mooduli aktiveerimine
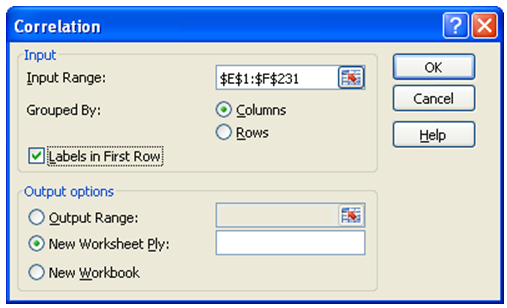
Avanevas tellimisaknas (pilt 2) on järgmised valikuvõimalused.
„Input Range“: Valida tunnused korrelatsioonimaatriksisse (valitavad tunnused peavad asuma andmestikus üksteise kõrval). Valime praeguses näites veerud E ja F ehk füüsiline aktiivsus ja koht ühiskonnas.
Praegusel juhul on tunnused grupeeritud veergudesse („Grouped By: Columns“) ja esimesel real on tunnuse nimed („Labels in First Row“).
Tulemused paneme uuele töölehele („New Worksheet Ply“).
Väljundis (tabel 1) antakse korrelatsioonimaatriksis tunnustevaheline lineaarne korrelatsioonikordaja (0,10494), mis näitab nõrka positiivset seost füüsilise aktiivsuse ja enda ühiskondliku positsiooni vahel.
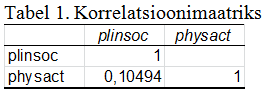
Kui esitatavaid korrelatsioonikordajaid on vähe, võib korrelatsioonanalüüsi tulemusi esitada teksti sees. Nt: analüüsi käigus selgus, et seos füüsilise aktiivsuse ja ühiskondliku positsiooni vahel oli nõrk (r=0,105).
Lisaks korrelatsioonikordajale võib esitada ka olulisuse tõenäosuse, vastajate arvu või vabadusastmete arvu. Nt: kaks tunnust olid omavahel tugevalt seotud, r=0,57; p<0,01.
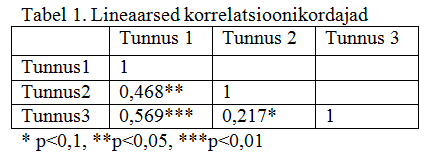
Juhul kui esitatavaid korrelatsioonikordajaid on rohkem, võib need koondada korrelatsioonimaatriksisse.
Tooding, L.-M. (2007). Andmete analüüs ja tõlgendamine sotsiaalteadustes. Tartu: Tartu Ülikooli Kirjastus.
Märksõnad: korrelatsioon, korrelatsioonikordaja, lineaarne korrelatsioonikordaja, astakkorrelatsioonikordaja, hajuvusdiagramm


