Regressioonanalüüsi põhiideid on mugav enesele selgeks teha paarisregressiooni juhul, mil vaatluse all on üks sõltuv ja üks seletav tunnus (nt inimese kaalu „seletamine“ pikkuse alusel). Regressioonanalüüs lähtub seosest sõltuva ja seletava tunnuse vahel. Kahe arvulise tunnuse vahel kasutame selle iseloomustamiseks enamasti Pearsoni korrelatsioonikordajat ja teame, et korrelatsioonikordaja mõõdab lähedusastet sirgjoonelisele (lineaarsele) seosele. Kuidas leida seda sirget? Otsitakse parimat lineaarset võrrandit sõltuva tunnuse Y ligikaudseks esituseks sõltumatu tunnuse ehk argumenttunnuse X kaudu järgmise skeemi kohaselt:

kus on prognostiline ehk mudelipärane sõltuva tunnuse väärtus ning regressioonikordaja b (ingl regression coefficient) ja vabaliige a (konstant, ingl intercept) määratakse andmete põhjal teataval parimal viisil. Indiviidi i, i = 1, 2, …, N korral tähendab see mudel seost:

kus e_i on mudeli viga ehk prognoosijääk, mis eeldatakse keskmiselt võrduvat nulliga (mudel on keskmiselt õige), ning X_i ja Y_i on vastavalt sõltuva ja seletava tunnuse väärtused selle indiviidi korral. Prognoositakse keskmiselt, statistilise suundumusena, keskeltläbi. Vea kohta tehakse hilisemate statistiliste otsustuste saamiseks teatud eeldusi: normaaljaotuse nõue, vea dispersiooni ühetaolisuse nõue. Tänapäevaste üldistatud lineaarsete mudelite korral on neid nõudeid ka oluliselt leevendatud.

Kordajate a ja b leidmine vähimruutude meetodil (ingl least squares) on üks sageli kasutatavaid võimalusi „parima“ mudelini jõudmiseks. Kordajad a ja b leitakse nii, et sõltuva tunnuse mudelipärase väärtuse hälbed tegelikust väärtusest ehk vead oleksid summaarselt minimaalsed:

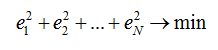
Arusaadavalt ei saa kõigi indiviidide vigu korraga minimeerida, sest regressiooniprognoos on n-ö kirik keset küla ehk kõigile korraga parim võimalik lahend, aga võib-olla mitte kellelegi eraldi parim. Tulemuseks on kordajate järgmised arvutusvalemid:

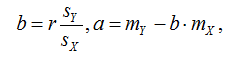
kus m_X ja m_Y on vastavalt tunnuste X ja Y keskmised ning s_X ja s_Y standardhälbed.

Joonisel 1 on toodud näiteid erisugustest sõltuvustest hajuvusdiagrammina ja kujutatud ka parim sõltuvusjoon sirge kujul ning esitatud äsjaste valemite abil saadud regressioonimudelid (sirge võrrandid). Ülemise rea skeemid vastavad positiivsele korrelatsioonile tunnuste vahel (sõltuvusjoon näitab trendi „alt vasakult paremale üles“) ja alumised negatiivsele (trend „vasakult ülevalt paremale alla“). Seose tugevus skeemidel väheneb vasakult paremale. Osutatud on ka vastava korrelatsioonikordaja ruut, mis näitab, kui suure osa ühe tunnuse muutlikkusest kirjeldab teine (vasakpoolseim skeem vastab perfektsele kirjeldusele).

Regressioonikordaja ja vabaliikme lihtsatest valemitest saame teha mõned põhimõttelised järeldused regressioonimudeli kohta. Kui tunnused on ühesuguse standardhälbega, siis regressioonikordaja võrdub korrelatsioonikordajaga, mis tähendab, et korrelatsioonikordaja on võtmesuurus regressioonimudeli leidmisel. Näeme ka, et regressioonivõrrand ei ole üldjuhul „pööratav“ ja tunnuse X avaldamiseks tunnuse Y kaudu tuleks võrrand koostada uuesti analoogiliselt äsjavaadelduga. Regressioonikordajate võimalik erinevus kahes eri suunas leitud mudeleis tuleneb tunnuste X ja Y suurusjärkude erinevustest.

Näide. Kaalu sõltuvus pikkusest Eesti sotsiaaluuringu 2007 andmeil, 5378 mehe ja 5444 naise andmed (vt http://www.stat.ee/77004).

Leiame regressioonikordajad eeltoodud valemite alusel.

Alusandmed meeste puhul (hajuvusdiagramm joonisel 2):

korrelatsioonikordaja r = 0,373,
pikkuse keskmine ja standardhälve: m_X = 178,2 cm, s_Y = 7,3 cm,
kaalu keskmine ja standardhälve: m_Y = 81,3 kg, s_Y = 14,2 kg,
regressioonikordaja: b = 0,373 ∙ (14,2:7,3) = 0,73,               
vabaliige: a = 81,3 – 0,73 ∙ 178,2 = 48,8.                  

Kaal pikkuse kaudu avaldub statistiliselt regressioonivõrrandiga:
Kaal = 0,73 Pikkus – 49.
Kui X = 178,2, siis keskmiselt Y = 0,73 ∙ 178,2 – 48,8 = 81,3 = m_Y. Näeme, et mudel on keskmiselt täpne, nagu peabki olema.
Kui näiteks X = 150 cm, siis Y prognoos on 0,73 ∙ 150 – 49 = 60,5 kg.
Kui näiteks X = 190 cm, siis Y prognoos on 0,73 ∙ 190 – 49 = 89,7 kg.
NB! Ettevaatust prognoosimisega! Mudel on empiiriline ja näitab seaduspära tunnuste vahel üksnes andmeile vastavas skaalaosas. Prognoosimine sellest kaugele väljapoole (ekstrapoleerimine) võib anda vale tulemuse.

Alusandmed naiste puhul:
korrelatsioonikordaja r = 0,169,
pikkuse keskmine ja standardhälve: m_X = 164,8 cm, s_Y = 6,3 cm,
kaalu keskmine ja standardhälve: m_Y = 68,9 kg, s_Y = 14,2

Mudel naiste kaalu prognoosimiseks tuleb (arvutage ka ise):
Kaal = 0,38 ∙ Pikkus + 6,3.

Millise sisu saab anda regressioonikordajale ja vabaliikmele? Regressioonikordaja b näitab sõltuva tunnuse muudu suurust keskmiselt, kui argument muutub ühiku võrra. Tõepoolest, sõltuva tunnuse muut argumendi muutumisel ühiku võrra on:

                        Y(X+1) – Y(X) = [a + b (X + 1)] – (a + b X) = b.

Meie näites tähendab ühe sentimeetri suurune erinevus naiste puhul keskmiselt 0,4 kilo suurust vahet kaalus ja meeste puhul keskmiselt 0,7 kilo suurust vahet. Regressioonikordaja märk näitab muudu suunda: plussmärk sõltuva tunnuse kasvu ja miinusmärk kahanemist sõltumatu muutuja kasvades. Kui regressioonikordaja on null, siis argumenttunnusel lineaarse mudeli alusel mõju sõltuvale tunnusele puudub. Kui korrelatsioonseos puudub, siis tuleb regressioonikordaja null.

Vabaliige a võrdub sõltuva tunnuse mudelipärase väärtusega, kui argument võrdub nulliga. Geomeetriliselt (meenutage gümnaasiumist sirge võrrandit) see on lõik püstteljel nullpunktist regressioonisirge lõikepunktini püstteljega, kui seletav tunnus võrdub nulliga. Meie näites joonisel 2 on lõikepunktiks 49 kg. Vabaliige ei ole sisuliselt tõlgendatav, kui argumendi väärtuste seas ei ole nullväärtust (meie pikkuse-kaalu näide on just säärane ja vabaliige kujutab endast lihtsalt teatavat võrrandi pooli tasakaalustavat tegurit). Vabaliikme tõlgenduse saavutamiseks andmed sageli eelnevalt tsentreeritakse (igast väärtusest lahutatakse maha kogumi keskmine).

Kui mudel on koostatud valimi alusel (meie näites 11 000 juhuslikult valitud inimest — tavatult suur hulk, kuid siiski osa tervikust), siis tekib küsimus, kuivõrd usaldusväärselt saab kinnitada regressiooniseose kehtivust populatsioonil. Kas populatsioonil võiks regressioonikordaja olla ka 0 ja seletava tunnuse ehk pikkuse muut ei tooks keskmiselt kaasa sõltuva tunnuse ehk kaalu muutust leitud seaduspära kohaselt?

Üks võimalusi regressioonikordaja statistilise usaldusväärsuse kontrolliks on vaadelda regressioonikordaja usaldusvahemikku. Kui regressioonikordaja usaldusvahemik ei kata väärtust null, siis võime kasutatava usaldusnivoo kohaselt käsitleda seletava tunnuse mõju statistiliselt usaldusväärsena terve populatsiooni jaoks.

Teine võimalus on testida hüpoteesi „tunnuse regressioonikordaja populatsioonis võrdub nulliga“. Selle hüpoteesi kontrollimiseks kasutatakse ligikaudset tulemust, mille kohaselt kordaja nulliga võrdumisel üldkogumis on kordaja ja selle standardhälbe suhe ligikaudu normaaljaotusega (väikese valimi korral t-jaotusega). Kui see suhe on väärtuse poolest vastuolus normaal- või t-jaotusega, siis tuleb hüpotees kummutada ja kordaja lugeda nullist erinevaks.

Regressioonimudeli statistilise usaldusväärsuse kontrollimiseks toetub tavauurija enamasti arvutist saadud tulemustele, mistõttu pikkuse-kaalu näitega isetehtud arvutuste varal me edasi ei lähe ja vaatleme seda küsimust uuesti peatüki lõpunäites.

Mudeli sobivuse ja tähtsuse hindamisel on vaja arvesse võtta mitut külge ning eelkõige silmas pidada, milleks mudel on koostatud. Kui oluline on prognoosi täpsus, siis tahaksime, et vead oleksid võimalikult väikesed. Kui huvi on üldise mõju laadi vastu, siis võime statistilises usaldusväärsuses järele anda jne. Seepärast on tähtis mudeli formaalsete statistiliste parameetrite puhul enesele selgeks teha, mis külge üks või teine neist peegeldab. Kõik mudeli kvaliteedi näitajad on harva korraga head. Veel on tähtis aru saada, et mudeli põhilisim omadus on tõlgendatavus. Kui formaalsed parameetrid on suurepärased, aga meil ei õnnestu anda regressioonikordajatele mõtet ei teoreetilise mudeli ega ka terve mõistuse abil, siis on meil mudelina saadud ainult teatav statistiline konstrukt, ei muud.

Regressioonikordajate (ja tervikmudeli) statistiline usaldusväärsus tuleb, nagu lubatud, veel kord kõneks allpool. Nagu üldiseltki statistilise järelduse puhul, on ka regressioonimudeli puhul oluline eristada statistilist usaldusväärsust ja sisulist kaalu.

Regressioonimudel luuakse selleks, et taandada sõltuva tunnuse muutlikkus seletava tunnuse muutlikkuseks, väljendada üht dispersiooni teise kaudu. Mudeli kvaliteedi oluline mõõt on see, kui suure osa sõltuva tunnuse dispersioonist saame seletada teise või teiste tunnuste kaudu. Teame, et korrelatsioonikordaja ruudus ehk determinatsioonikordaja väljendab seda, kui suure osa dispersioonist kirjeldavad tunnused vastastikku. Determinatsioonikordajat R² saab esitada veel teisiti (sobib ka meie käsitluse hilisemaks juhuks, mil seletavaid tunnuseid tuleb mudelisse sisse mitu), nimelt kui regressioonisirgega „seletatud“ dispersiooniosa suhet sõltuva tunnuse kogudispersiooni:

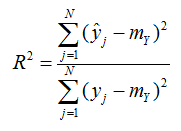
Selles avaldises (meenutage tähistusi eestpoolt, vt paarisregressiooni mudel) on murru lugejas kesksel kohal vahed , mis väljendavad seda, kui palju erineb mudelipärane individuaalne prognoos sõltuva tunnuse keskmisest. Seega näitab vahe, kui palju „seletas“ argumenttunnus täiendavalt sõltuva tunnuse variatiivsust ja parandas keskmist kui iga indiviidi jaoks kõige lakoonilisemat prognoosi. Kui me ei tea indiviidist mitte midagi, siis parema puudumisel omistame talle tõepoolest sõltuva tunnuse keskmise taseme. Kui aga teame lisaks mõnd täiendavat tunnust, siis võime saada parema prognoosi. Kui palju parema, seda näitabki kõnealune vahe. Determinatsioonikordaja on suhteline mõõt ja suhestab kõigi indiviidide poolt kokku „seletatud“ variatiivsuse määra sõltuva tunnuse dispersiooniga (murru nimetajas olev ruutude summa). Miks ruudud? Meid ei huvita, kas vahed on pluss- või miinusmärgiga, meid huvitab, kui tugev on kõrvalekalle keskmisest.

Meie pikkuse-kaalu näites tuleb naiste puhul determinatsioonikordaja 3% ja meestel 14%. Mida sellest arvata, kuidas sisuliselt mõista kirjeldusmäära? Joonisel 3 on kujutatud vasakul mudelipäraste kaaluprognooside jaotust ja paremal tegelikku jaotust. Keskmine on mõlemal muutujal sama, aga standardhälbed ehk hajuvuse määrad erinevad. Prognooside standardhälve on peaaegu kolm korda väiksem kui kaalutunnusel tegelikult, vastavalt 5,3 kg ja 14,1 kg. See ongi ainult 14% suuruse ehk mittetäieliku kirjeldusmäära mõte – mudel ei suuda peegeldada sõltuva tunnuse variatiivsust täiel määral ja näidata mehi kaalu poolest sellise eripäraga, nagu nad on tegelikult. Naiste puhul on pilt veel teravam (vt joonis 4). Kui tegelikult varieerub naiste kaal silma järgi 40 ja 120 kilo vahel (standardhälve 14,2 kg), siis 3% suuruse kirjeldusastmega mudel paigutab enamiku naistest 65 ja 75 kilo vahele (standardhälve 2,4 kg).

Regressioonimudeli kvaliteedi analüüsimisel on olulisel kohal vead ehk prognoosijäägid: funktsioontunnuse tegelik väärtus miinus mudelipärane prognoos. Jääkide keskmine on null ja mida väiksem on jääkide standardhälve, seda parem, seda vähem erinevad jäägid nullist ehk seda täpsem on prognoos. Jäägi märk miinus näitab, et tegemist on ülehindamisega (indiviidile prognoositakse suurem väärtus, kui on tegelikult), ja pluss viitab alahindamisele (prognoos on väiksem kui väärtus tegelikult). Eriti tähtis on vaadelda suuri jääke, mis võivad anda teada kas vigadest andmeis (saime mõttetult ebatüüpilise prognoosi) või iseärastest indiviididest ehk erinditest (leidsime uunikumi). Regressioonimudelite korral segavad teistest tugevalt väljaulatuvad väärtused üldise keskmise trendi esiletoomist ja seetõttu jäetakse nad mudelist tavaliselt kõrvale. Ettevaatust – mudelist kõrvalejätmine ei muuda neid olematuks ja erindid võivad anda väga tähtsat lisainfot üksikanalüüsil.

Tabelis 2 on esitatud meie näite puhul tavapärane mudeli prognoosijääkide statistika eraldi meeste ja naiste jaoks. Prognoosid on keskmiselt õiged ja nende standardhälve väiksem kui sõltuval tunnusel tegelikult (meestel 5,3 kg 14,2 kg kõrval, naistel 2,4 kg 14,2 kg kõrval). Prognoosijäägid võrduvad keskmiselt nulliga. Näeme, et vigade standardhälve on naistel pisut suurem kui meestel (vastavalt 14,0 kg ja 13,1 kg) ehk prognoosid on naistel pisut ebatäpsemad kui meestel.

Kaalu prognoosid eespool vaadeldud kujul oma madala kirjeldusastmega vaevalt et kedagi huvitaksid. Vaja oleks arvesse võtta veel paljusid kõrvaltegureid: töö iseloom, toitumisharjumused, elulaad jne. Selline samm üldistuse poole on regressioonimudeli kasutaja jaoks õnneks lihtsam kui matemaatiku jaoks, kes vastavat mudelit välja arendab. Korrates paljuski äsjaräägitut, esitame alljärgnevalt paarisregressiooni mudeli üldistuse enam kui kahe seletava tunnuse juhule ehk mitmese regressioonimudeli juhule.

Uurigem sõltumatute tunnuste X₁ , X₂,… X_m mõju sõltuva tunnuse Y variatiivsuse kujunemisel mudeli

 = b₀ + b₁X₁ + b₂X₂ + … + b_mX_m

kohaselt. Mudeli vead eeldatakse olevat keskmiselt võrdsed nulliga, normaaljaotuse kohased ja ühetaolise dispersiooniga.

Kordajad b₀ , b₁, b₂ , …, b_m leitakse teatud optimaalsuse nõudest lähtuvalt. Näiteks vähimruutude meetodi korral seatakse eesmärgiks minimeerida prognoosijääkide ruutude summa.

Regressioonimudeli koostamise aluseks on endiselt idee seletada võimalikult suurt osa sõltuva tunnuse variatiivsusest sõltumatute tunnuste kaudu. Kirjelduse mõõduks on analoogiliselt paarisregressiooni juhuga determinatsioonikordaja, mis mõõdab, kui suurt osa sõltuva tunnuse variatiivsusest katavad regressiooniprognoosid. Ruutjuurt determinatsioonikordajast tuntakse kui mitmest korrelatsioonikordajat (ingl multiple correlation coefficient; paarisregressiooni juhul: korrelatsioonikordajat). Mitmene korrelatsioonikordaja sõltuva tunnuse ja seletavate tunnuste vahel on sisuliselt paariskorrelatsioonikordaja sõltuva tunnuse ja sõltuva tunnuse prognoosidest moodustatud tunnuse vahel. Tõepoolest, prognoosides kajastub seletavate tunnuste variatiivsus. Mida parema prognoosi mudel annab, seda tugevamalt on omavahel korreleeritud prognoos ja prognoositav.

Regressioonikordaja formaalne tõlgendus on analoogiline paarisregressiooniga: regressioonikordaja näitab sõltuva tunnuse keskmist muutu kordajale vastava sõltumatu tunnuse ühikulise muudu korral, kui ülejäänud sõltumatud muutujad on püsiva väärtusega. Vabaliige näitab keskmist prognoosiväärtust kõigi argumentide nullkohas.

Mitmese regressioonimudeli korral tekib vajadus võrrelda seletavaid tunnuseid mõju tugevuse poolest. Regressioonikordajate alusel ei ole see võimalik, sest tunnused on tavaliselt erisuguse skaalaga ja erisuguse variatiivsusega. Sellele vastavalt on ka regressioonikordajad „kalibreeritud“ erisuguselt, et lõppkokkuvõttes tuleks välja sõltuva tunnuse suurusjärku väärtus. Et võrrelda ühe mudeli (andmestiku) piires seletavate tunnuste toimet, arvutatakse tavaliselt ka nn beeta-kordajad ehk standardiseeritud regressioonikordajad. Need leitakse andmestikul, mis saadakse mudelis osalevate tunnuste eelneva standardiseerimise teel, ehk olukorras, kus kõik tunnused on ühetaolisel skaalal keskmisega 0 ja standardhälbega 1, seega võrreldavate regressioonikordajatega. Standardiseerimine tähendab väärtuste tsentreerimist tunnuse keskmise suhtes selles kogumis ja tsentreeritud väärtuse väljendamist tunnuse standardhälbe ühikutes.

Matemaatiliselt asendub regressioonikordajate leidmisel mitmese regressioonimudeli puhul korrelatsioonikordaja osakorrelatsioonikordajaga (ingl partial correlation), õigemini pseudo-osakorrelatsioonikordajaga (ingl part correlation), mis peegeldab tunnuse „puhast“ mõju sõltuva tunnuse variatiivsuse kirjeldamisel, elimineerides selle mõju osa, mis toimib teiste mudelisse võetud tunnuste kaudu (Tooding 2007, p 6.2.2 või viide [Seoste analüüsimine]). Võime ette kujutada, et ka seletavate tunnuste eneste seas peitub teatud võimalus ühe statistiliseks väljendamiseks teiste kaudu. Regressioonikordajana tahame näha siiski arvu, mis näitab selle tunnuse eriomast mõju sõltuva tunnuse variatiivsuse kirjeldamisel. Et hinnata tunnuse „isiklikku“ panust mudelis, tuuakse mõnikord esile tunnuste tolerantsikordajad. Tolerantsikordaja (ingl tolerance) mõõdab, kui suur on seletava tunnuse dispersioonis selle tunnuse poolt kirjeldatud, kuid ülejäänud tunnuste poolt kirjeldamata osa. Mida kõrgem on tolerants, seda paremini sobib tunnus mudelisse (nagu tolerantne inimenegi seltskonda). Kõigi tunnuste kõrge tolerants on tunnusmärk, et tunnuste vahel ei valitse multikollineaarsust ehk ühe tunnuse ilmekat avaldumist teiste lineaarkombinatsioonina (teiste kaalutud summana).

Täiesti loomulik on, et sisuliselt võib olla tarvis kaasata seletavate tunnustena ka mittearvulisi tunnuseid (nt kaalu puhul elulaad, elukoht, amet). Selleks on mitmeid skeeme, mida kõiki ühendab üks idee: lisada mudelisse kategoriaalse tunnuse asemel teatud hulk abitunnuseid, mis annavad edasi kategoriaalse tunnuse kogu informatsiooni. Teiste sõnadega, kategoriaalne tunnus kodeeritakse teatud viisil ümber. Vaatleme nn indikaatorkodeerimist, mil tekitatakse kategooriate arvust ühe võrra vähem dihhotoomseid tunnuseid (ingl dummy variables).

Näiteks saab elukohta Eesti viiest piirkonnast koosneval skaalal edasi anda nelja dihhotoomse indikaatortunnuse abi1, …, abi4 kaudu, mis väärtustatakse järgmiselt:

                                    abi1     abi2     abi3     abi4

Põhja-Eesti                  1          0          0          0        
Lääne-Eesti                 0          1          0          0
Kesk-Eesti                   0          0          1          0
Kirde-Eesti                  0          0          0          1
Lõuna-Eesti                0          0          0          0

Abitunnuseid võib olla tõepoolest ühe võrra vähem, sest ühe (praegusel juhul viimase) kategooria tunneme ära sellest, et kõik indikaatortunnused võrduvad nulliga. See on nn taustakategooria (ingl reference category) ja selle valik on üldiselt vaba. Valik tehakse tähenduse järgi, piisavalt suure indiviidide arvuga esindatuse jm kaalutlustel. Mudeli koostamise järel saadakse iga kategooria jaoks teada oma regressioonikordaja, mis on siinkirjeldatud abitunnuste kordajad regressioonimudelis. Taustakategooria jaoks võetakse regressioonikordaja võrdseks nulliga. Teisiti öeldes, tegemist on tunnuse kategooriatele vastavate regressioonikordajatega taustakategooria suhtes. Just nimelt seda – teatavat suhtelist meetrikat – meil vaja ongi, sest kategoriaalsel tunnusel ei ole ei nullpunkti ega muud suuruse mõõdupuud.

Näide põhineb Euroopa sotsiaaluuringu 2010. aasta andmetel Eesti, Soome ja Venemaa kohta. Ülesandeks on uurida sisserände mõju üldistatud hinnangute olenevust vanusest, elukohamaast, oma maa parlamendi ja Europarlamendi usaldusastmest. Tunnuste tähenduse ja andmetega on võimalik tutvuda aadressilt http://www.yti.ut.ee/et/euroopa-sotsiaaluuring lähtudes.

Sisserände hinnang on saadud kolme hinnangutunnuse keskmisena (tunnus Immigration): immigrantide arvatav mõju majanduselule, kultuurielule ja elule üldiselt mõõdetuna skaalal 0 kuni 10. Mida suurem väärtus, seda positiivsem mõju arvatakse olevat. Ka parlamentide usaldushinnanguid mõõdeti analoogilisel skaalal nullist kümneni ehk usalduse täielikust puudumisest kuni täieliku usalduseni. Tabelis 3 on esitatud kõigi tunnuste ülevaade keskmiste ja standardhälvete kaudu (vältimatu osa regressioonimudeli koostamisel) ja tabelis 4tunnustevahelised korrelatsioonikordajad. Maa tunnust kaasates eeldame alljärgnevas mudelis, et sõltuva tunnuse keskmine võib olla eri maades erisugune, kuid seletavate tunnuste mõju mehhanism mitte (leitakse üks ühine regressioonikordaja kolme maa jaoks; mudeli edasiarendamise võimalus oleks nt maa ja teiste tunnuste interaktsioonide kaasamine, mis tähendaks ka selle võimaluse lubamist, et mõju mehhanism on eri maades erisugune, vt Tooding, p 6.4.2). Regressioonikordaja väljaarvutamisel peetakse matemaatilises algoritmis korraga silmas kõiki tunnuseid, mis on mudelisse võetud.

Eestist pärit vastajaid on vaadeldavate tunnuste korral 1926, Soomest 2089 ja Venemaalt 1734. Kasutati loetelupõhist andmelünkadega indiviidide kõrvalejätmist. Arvutused on tehtud paketiga SPSS.

Sisserände mõju hinnang on keskmiselt 5 punkti ehk skaala füüsilises keskpunktis (vt tabel 2), parlamentide hinnangud on sellest pisut allpool. Nagu näeme sisserände koondhinnangu histogrammilt jooniselt 5, on hinnangutes üsna ohtralt kasutatud mugavusvastust „5“. Teine oluline tähelepanek – märkame pooleteisesaja ringis absoluutseid nullhinnanguid kõigi kolme sisserände mõju üksikhinnangu alusel ja ka need ei ole nähtavasti väga asjakohased andmed, vaid peegeldavad pigem üldist vastuseisu sisserändele.

Sisserände koondhinnangu korrelatsioonseos parlamentide usaldushinnangutega on mõõdukalt positiivne (vt tabel 4), kuid korrelatsioonseos vanusega on väga nõrk (seejuures negatiivne ja statistiliselt usaldusväärne olulisuse tõenäosuse 11% korral, ülejäänud korrelatsioonikordajate statistiline usaldusväärsus on kõrgem). Võib kahtlustada, et maid eraldi vaadeldes võiks seos vanusega olla maade kaupa ka erisugune, sest Soomes on sisserände kogemus pikaajaline, kahel ülejäänud maal peaaegu puudub. Seletavate tunnuste omavahelisest korrelatsioonseosest torkab silma meie mudeli suhtes kahtlustäratav tõsiasi: Euroopa parlamendi ja oma maa parlamendi hinnangute omavaheline korrelatsioon on 0,6 ringis, mida pole vähe. Kas võib olla tegemist olukorraga, kus üks hinnang on ennustatav teiste kaudu ja seega ei peegelda regressioonikordaja tunnuse ees selle tunnuse eriomast mõju? Siiski lähme oma lahendusega lõpuni, et tolerantsikordajate abil ka sellele küsimusele vastus saada.

Lisame siia veel lähteinfoks sõltuva tunnuse ehk sisserände koondhinnangu keskmised kolmel maal (sulgudes standardhälve): Eestis 5,1, (1,9), Soomes kõrgeim 6,1 (1,7) ja Venemaal madalaim 3,6 (2,1).

Vaatleme esmalt, kui suurt osa sisserände hinnangute dispersioonist saab kirjeldada siin vaadeldavate seletavate tunnuste kaudu. Tabel 5 on traditsioonikohase ülesehitusega dispersioonanalüüsi tabel, millest selgub sõltuva tunnuse dispersiooni jagunemine kaheks: ärakirjeldatud ja kirjeldamata osaks. Arvepidamine toimub keskmise suhtes leitud summaarsete ruuthälvete kaudu. Reas „regressioon“ on summaarse ruuthälbe ärakirjeldatud osa (7897) ja reas „jääkhajuvus“ kirjeldamata jäänud osa. Kirjeldatud osa suhe summaarsesse ruuthälbesse tervikuna (26 771) annabki mudeli kirjeldusmäära ehk determinatsioonikordaja, mis on praegu 29,5% ehk 0,295 = 7897 : 26771. Mitmene korrelatsioonikordaja ehk korrelatsioonikordaja sõltuva tunnuse ja mudeli kohaste prognooside vahel on seega 0,54 – ei vähe ega palju, kui arvestada, et korrelatsioonikordaja miinimum on null ja maksimum 1.

Dispersioonanalüüsi tabel võimaldab testida ka saadud mudeli terviklikku statistilist usaldusväärsust ehk hüpoteesi: mudeli poolt ärakirjeldatud osa dispersioonist on tühine. Selleks leitakse summaarne ruuthälve ühe vabadusastme kohta ehk ruutkeskmine hälve. Vabadusastmete arvud on määratud vastavalt hinnatavate regressioonikordajate arvu (kuus regressioonikordajat, k.a vabaliige) ja indiviidide arvu kaudu, lahutades kummastki ühe. Ruutkeskmist hälvet võib mõista kui keskmist seletatud osa ühe regressioonikordaja suhtes ja jääkhajuvust ühe indiviidi suhtes. Saab näidata, et nende kahe arvu suhe ehk F-suhe on nimetatud hüpoteesi eeldusel ligikaudu teoreetilise F-jaotusega regressioonikomponendi ja jääkhajuvuse vastavate vabadusastmete arvude korral (praegu 5 ja 5745 puhul). Hüpoteesi olulisuse tõenäosus on väga väike, kindlasti alla 0,0005 antud täpsuse korral (ei riskiks öelda, et 0, sest kaugemates komakohtades võib olla nullist erinevust). Seega on alust hüpotees kummutada ja lugeda mudeli kirjeldusvõime statistiliselt usaldusväärseks olulisuse tõenäosuse korral, mis on alla 0,05%. Niisiis, on põhjust minna mudelit uurima. Tegelikult tasub seda teha ka juhul, kui statistiline järeldus ei oleks nii soodus, nt kui olulisuse tõenäosus on väheldane, aga mitte väike. Mudelist võib saada mõtteid ebaõnnestunud lahenduse parandamiseks või taibata, miks mudel, mis meie arvates peaks olema hea kirjeldusvõimega ja statistiliselt usaldusväärne, seda ei ole.

Tabelis 6 on sisserände mudeli tõlgendamiseks sobivad regressioonikordajad esitatud esimeses veerus (B). Nii näiteks saame öelda, et ühe punkti võrra kõrgem usaldus oma maa parlamendi suhtes tõstab sisserände mõju hinnangut keskeltläbi 0,15 punkti võrra, kui teiste tunnuste väärtused on samad, st sama vana indiviid samast riigist sama usaldusastmega Euroopa parlamendi suhtes. (Tabelis on täpsusega veidi üle pingutatud, piisaks kahest või koguni ühest kümnendkohast, aga olgu pealegi). Vanuse regressioonikordaja märk on miinus, mis tähendab, et iga lisanduv aasta, kui eri vanuses indiviide kõrvutada, langetab hinnangut immigrantidele keskmiselt 0,01 võrra, kui teised tunnused on samade väärtustega (siiski väga väike vahe). Eesti regressioonikordaja 1,34 tähendab seda, et Eestist pärit vastaja hinnang on keskmiselt 1,34 punkti võrra kõrgem kui praegu taustamaana kasutatavalt Venemaalt pärit vastaja oma, seda juhul, kui teised tunnused on ühetaoliste väärtustega. Soome vastaja prognostiline sisserände hinnang on keskmiselt ligi kaks punkti kõrgem kui Venemaal, kui muud tunnused on ühel ja samal tasemel.

Veerust „Beetakordajad“ näeme standardiseeritud regressioonikordajaid. Miks on vaja kasutada regressioonikordajaid ka veel standardiseeritud andmete kaudu? Veerust B saame küll teada, kui suur sõltuva tunnuse nihe kaasneb seletava tunnuse muuduga, aga ei oska öelda, kas see nihe on tähenduse poolest sõltuvale tunnusele väiksem või suurem kui mõne teise tunnuse puhul tekkiv muutus, sest seletavad tunnused võivad olla erisuguse skaala ja suurusjärguga. Teine lugu on standardiseeritud andmetega, mis on alati ja igatpidi suuruse poolest võrreldavad. Sellest tulenevalt on ka standardiseeritud regressioonikordajad suuruse poolest võrreldavad ja näitavad samamoodi sõltuva tunnuse keskmist muutu, aga ainult spetsiifilisel viisil – vastava tunnuse kõnealuses andmekogumis ilmneva standardhälbe ühikutes. Standardhälbe suurune ühik loob beetakordajate võrdluse võimaluse. Arve suuruse poolest võrreldes selgub, et suurimad vahed sisserände mõju hinnanguis tulenevad maadevahelistest erinevustest. Maa parlamendi usaldushinnang on seejuures praeguse pildi kohaselt tugevam mõjutegur kui Euroopa parlamendi hinnang. Vanuse mõju on teiste tunnustega võrreldes õhkõrn.

Nägime eespool, et mudel tervikuna on statistiliselt kõrge usaldusväärsusega olulisuse tõenäosuse korral alla 0,05%. See ei tähenda automaatselt, et kõik seletavad tunnused on statistiliselt usaldusväärse mõjuga. Pilk olulisuse tõenäosuste veergu laseb siiski arvata, et käesoleval juhul on küll, seejuures sama väikese olulisuse tõenäosusega. Kuidas selle üle otsustati? Nagu eespool paarisregressiooni juures juba osutasime, kasutatakse siinkohal t-statistikut (regressioonikordaja jagatud kordaja standardhälbega; arvutused tehti täpsemate arvudega, kui on tabelis näha). See peaks hüpoteesi „b = 0“ korral ehk olukorras, kus seletav tunnus on mudelis populatsiooni korral mõjuta, jaotuma t-jaotuse kohaselt. See hüpotees ei pea praegu ilmselgelt paika, sest iga tunnuse puhul on hüpoteesi olulisuse tõenäosus väga väike (kindlasti alla 0,05%). Siiski ei tasu pidada silmas ainuüksi kõrget statistilist usaldusväärsust, vaid lähtuda esmajoones ikkagi regressioonikordajast, mis annab käegakatsutava ettekujutuse sellest, kui tugev on seletava tunnuse toime. Praegu on indiviidide arv niivõrd suur, et iga vähimgi mõjuke näib statistiliselt olulisena. Nii see paraku sageli ongi hüpoteeside kontrolli loogika kohaselt.

Kindlasti tuleks vaadelda regressioonikordaja usaldusvahemikke, millest praegu mitte ükski ei kata nullpunkti. Kui kataks, siis oleks nulliga võrduv regressioonikordaja populatsioonis suure tõepärasusega võimalik ja tunnuse statistiline mõju sõltuva tunnuse suhtes puuduks. Et usaldusnivooks on valitud 95%, siis sellise usaldusväärsusega saaksime praegu usaldusvahemike alusel igat tunnust eraldi käsitledes kinnitada selle statistilist mõjukust. Miks „eraldi käsitledes“? Rõhutame seda nn Bonferroni efekti kartuses: üksikotsustuse usaldusväärsus ei taga mitmest otsustusest koosneva lõppotsustuse sama kõrget usaldusväärsust, sest ühel ja samal andmestikul põhinedes võivad statistilised vead kuhjuda. Turvaline oleks üksikotsustused teha kõrgemal usaldusnivool, seda kõrgemal, mida enam otsustusi on korraga kõne all. Jälgige ka usaldusvahemiku laiust (mida kitsam, seda konkreetsem hinnang) ja seda, kui „kaugel“ on nullpunkt (ehk olematu mõju punkt) usalduspiiridest.

Tuleme nüüd tagasi eespool kripeldama jäänud multikollineaarsuse teema juurde. Kui arvutada välja tolerantsikordajad (ei ole regressioonimudeli tabelis esitatud), siis leiavad kahtlused kinnitust: vanuse tolerantsiaste tuleb kõrge (97%), aga oma maa parlamendil ja Euroopa parlamendil madal (vastavalt 55% ja 63%). Mõned peavad 60% läve kriitiliseks, igatahes võiks meie näites ühe parlamendi usaldushinnangutest kõrvale jätta. Et oma maa parlamendi usaldusastme hinnanguis on vastustes lünki vähem, siis jätame selle tunnuse mudelisse. Kaalutluseks võiks olla veel muidugi sisuline külg või ka tolerantsikordaja väärtus või tunnuse korrelatsioonikordaja sõltuva tunnuse suhtes (Euroopa parlamendil madalam kui oma maa parlamendil, vt tabel 4).

Koostame uue mudeli, milles ei osale Europarlamendi usaldushinnang (vt tabel 7). Indiviidide arv suurenes, olles nüüd 6341. Mudeli kirjeldusvõime alanes 28% tasemele, mis ei ole suur kadu (enne oli 29,5%). Mudel tervikuna ja kõik üksikkomponendid (dispersioonitabelit ei ole selle mudeli jaoks esile toodud) jäid statistiliselt usaldusväärseiks olulisuse tõenäosuse korral alla 0,05%. Ühegi kordaja usaldusvahemik usaldusnivool 95% ei kata nullpunkti. Kõigi seletavate tunnuste mõju suund jäi samaks ja tugevus ligikaudu samaks, nagu oli enne. Oma maa parlamendi usaldusastme tolerantsikordaja väärtuseks osutus selles mudelis 82% ja selle mudeli juurde jäämegi.

Formaalselt võiksime välja kirjutada järgmised prognoosimudelid:
Eesti jaoks:
Immigratsiooni mõju hinnang = 3,44 + 0,21∙ parlamendi usaldushinne – 0,01∙ vanus + 1,44
Soome jaoks:
Immigratsiooni mõju hinnang = 3,44 + 0,21∙ parlamendi usaldushinne – 0,01∙ vanus + 2,05
Venemaa jaoks:
Immigratsiooni mõju hinnang = 3,44 + 0,21∙ parlamendi usaldushinne – 0,01∙ vanus

Erinevus maade vahel, nagu oli käesoleva näite puhul kavandatudki, peitub keskmises tasemes, mitte mõju mehhanismis, ja seletavate tunnuste kohta kasutame eri maades ühtesid ja samu regressioonikordajaid.

Vaatleme lõpuks põgusalt prognoosi täpsust prognoosijääkide kujul. Joonisel 6 on esitatud standardiseeritud prognoosijääkide histogramm, millest näeme üsna head kooskõla normaaljaotusega, vähemalt palja silmaga (peen sujuva väljanägemisega joon vastab ideaalsele normaaljaotusele keskmise 0 ja standardhälbe 1 korral). Standardiseeritud kujul jäävad vead selgelt –3 ja 3 vahele, mis normaaljaotuse korral juba gümnaasiumist tuntud kolme sigma reegli alusel nii peabki olema.

Formaalseid eeltingimusi

n  Seletavad tunnused on korreleeritud sõltuva tunnusega.
n  Seletavate tunnuste seas ei ole omavahel tugevalt lineaarselt seotud tunnuseid (multikollineaarsuse välistamine).
n  Seletavate tunnuste mõju sõltuvale tunnusele on oma iseloomu poolest liituv ja lineaarne (seos väljendub sirgjoonega). Nt ruumi ümbermõõdule mõjub ruumi pikkus liituvalt ehk aditiivselt, aga pindalale mitte (mõjub korrutislikult ehk multiplikatiivselt).
n  Sõltuv tunnus on fikseeritud arvulisel või arvuliselt tõlgendataval skaalal.
n  Mudeli vea jaotus on lähedane normaaljaotusele ja ühetaolise dispersiooniga vaadeldavate tunnuste väärtuspiirkonnas.

Mitmese lineaarse regressioonimudeli koostamine: soovitatavalt hierarhiliselt

Algaja regressioonimudeli kasutaja armastab kaasata korraga palju seletavaid tunnuseid ja soovitatavalt kõik korraga. Kõige hullemal juhul laseb ta siis arvutiprogrammil nn sammuviisilise protseduuriga (ingl stepwise regression) ise valida, mida võtta, mida jätta. Professionaal nii ei tee, sest selliselt on vähe lootust jõuda sisuliselt vettpidava mudelini. Soovitatav on kõigepealt pikemalt tegelda aineteoreetiliste kaalutlustega ja läbi mõelda, millised seletavad tunnused võiksid kõne alla tulla. Seejärel tuleks need läbi uurida lihtsate statistiliste suuruste varal (keskmised, korrelatsioonid, jaotused, graafikud). Väljasõelutud tähtsaid seletavaid tunnuseid oleks mõistlik lülitada mudelisse ühekaupa, tekitades niiviisi järjest keerulisemaks muutuvate mudelite hierarhia. Järjestikuste mudelite kirjeldusastmete võrdlus annab olulist teavet mudelisse võetud tegurite mõjukuse kohta. Jälgida tuleks ka regressioonikordajate stabiilsust: kui palju muutuvad seniste seletavate tunnuste regressioonikordajad, kui mängu tuleb uus mõju.

Mitmese lineaarse regressioonimudeli tõlgendamisest

n  Sotsiaalteaduslike andmete (mittekatseliste andmete) puhul on regressioonimudeli tõlgendus sageli pigem kvalitatiivne, seoste struktuuri kirjeldav kui kvantitatiivset prognoosi taotlev.
n  Vaadelda tuleb
n seletava tunnuse mõju suunda, kas selle kasv kahandab või kasvatab sõltuvat tunnust,
n sõltumatute tunnuste järjekorda mõju tugevuse poolest (beetakordajad),
n mõjude sisulist mõistlikkust,
n mudelist hälbivate indiviidide loetelu (suured jäägid),
n mudeli üldist kirjeldusastet ja mitmest korrelatsioonikordajat.

Reaalteaduslike uurimisülesannete korral on kohane ka mudeli tõlgendus prognoosimehhanismina.

Regressioonimudeli koostamisel tekib hulk eritasemelisi statistilisi kokkuvõtteid, mille hulgast uurimistöösse sobiva valimine on paras pähkel. Lähtuda tuleks, nagu mujalgi, uurimisküsimusest ja auditooriumist. Allpool on näide võimalikest valikutest.

Populaarteadusliku loo puhul võiks joonistada uurimisobjekti efektse sisendite-väljundite pildi, millest nähtuks ka sisendite statistiline kaalukus (jämedamad-peenemad nooled vms).

Laiema akadeemilise auditooriumi jaoks tuleks anda ülevaade andmetest (kompaktne keskmiste, standardhälvete jm tabel) ja esitada regressioonimudel tabelina, milles miinimumversioonis on regressioonikordajad koos statistilise olulisusega või usaldusvahemikega mingil usaldusnivool. Beetakordajatest nähtuva järjekorra võiks selgitada teksti sees, samuti mudeli üldise kirjeldusastme.

Asjatundlikumale akadeemilisele auditooriumile võivad huvi pakkuda veel kordajate standardhälbed, beetakordajad ka arvuliselt ja detailsemalt dispersioonitabel.

Kindlalt tuleb meeles pidada seda, et ühegi töö keskseks osaks ei ole mitte arvulised kokkuvõtted, vaid neist tulenev tõlgendus, arvude tähendus.

http://www.ats.ucla.edu/stat/spss/webbooks/reg/chapter1/spssreg1.htm
Tooding, L.-M. (2007). Andmete analüüs ja tõlgendamine sotsiaalteadustes. Tartu, Tartu Ülikooli Kirjastus. Ptk-d 5.3, 6.2.