
Sotsiaalse Analüüsi Meetodite ja Metodoloogia õpibaas
Bayesi statistika
Taavi Unt
2020
Statistikas on eristatavad kaks peamist koolkonda: Bayesi statistika ja sagedusstatistika ehk nn klassikaline statistika. Mõlemal juhul on eesmärk olemasolevate vaatluste (valimi) pealt hinnata kogu populatsioonis kehtivaid seoseid või huvipakkuvaid näitajaid. Teisisõnu soovitakse hinnata parameetrit θ (theta), mis võib olla nii arv (nt üldkogumi keskmine) kui vektor (nt regressioonanalüüsi kordajad). Milles seisneb aga Bayesi ja sagedusstatistika erinevus? Erinevused tulenevad eelkõige filosoofilisest lähenemisest.
Sagedusstatistikud lähtuvad eeldusest, et andmete saamise protsess on korratav. Lisaks eeldatakse, et huvipakkuv parameeter θ ei ole küll teada, kuid on fikseeritud (konstant), ning vaatlusandmed on ainus teave, mida parameetri θ hindamisel kasutada.
Bayesi statistika seevastu ei nõua, et andmete genereerimise protsess oleks korratav. Kuigi lähte-eelduste kohaselt ei ole parameetri θ väärtus teada, eeldatakse see olevat kirjeldatav tõenäosuslikult (jaotusega). Parameetri θ kirjeldamisel kasutatakse nii vaatlusandmeid kui ka analüüsi läbiviija eelteadmisi parameetri kohta. Seejuures andmete abil täpsustatakse eelteadmisi.
Nii Bayesi kui sagedusstatistika puhul eeldatakse, et vaadeldavad andmed x on mingist parameetriga θ määratud jaotusest. Seda, kui hästi antud andmed erinevate parameetri θ väärtustega kooskõlas on, kirjeldab tõepärafunktsioon ![]() . Fikseeritud θ
. Fikseeritud θ korral nimetatakse funktsiooni f tihedusfunktsiooniks, kui vaatlused on pidevast jaotusest, või tõenäosusfunktsiooniks, kui vaatused on diskreetsest jaotusest (vt peatükki tunnustest ja nende tüüpidest).
Kui sagedusstatistika kohaselt on θ mingi tundmatu arv, siis Bayesi statistikas eeldatakse, et θ on juhuslik suurus. Eelteadmist parameetri θ kohta väljendatakse parameetri eeljaotusega ![]() . Eeljaotus võib seejuures sõltuda veel omakorda parameetri(te)st α. Tavaliselt eeljaotust tähistades seda ei rõhutata, kuid kui on vaja sellele siiski tähelepanu juhtida, võib eeljaotust tähistada kujul
. Eeljaotus võib seejuures sõltuda veel omakorda parameetri(te)st α. Tavaliselt eeljaotust tähistades seda ei rõhutata, kuid kui on vaja sellele siiski tähelepanu juhtida, võib eeljaotust tähistada kujul ![]() . Parameetrit α nimetatakse hüperparameetriks ning see fikseeritakse analüüsi läbiviija poolt vastavalt tema eelteadmistele uuritava parameetri θ kohta.
. Parameetrit α nimetatakse hüperparameetriks ning see fikseeritakse analüüsi läbiviija poolt vastavalt tema eelteadmistele uuritava parameetri θ kohta.
Selleks, et kombineerida analüütiku eelteadmisi (![]() ) ja andmetes sisalduvat informatsiooni (
) ja andmetes sisalduvat informatsiooni (![]() ), tuleb kasutada Bayesi valemit:
), tuleb kasutada Bayesi valemit: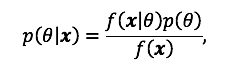
kus funktsiooni ![]() pθx nimetatakse parameetri
pθx nimetatakse parameetri ![]() järeljaotuseks. Funktsioon
järeljaotuseks. Funktsioon ![]() on andmete tihedusfunktsioon üle kõikvõimalike
on andmete tihedusfunktsioon üle kõikvõimalike ![]() θ väärtuste, st
θ väärtuste, st ![]()
Seega on meil olemas eeskiri, kuidas olemasolevaid andmeid arvesse võttes oma eelteadmisi täpsustada. Seejuures on sama eeskirja võimalik täiendavate andmete laekumisel korduvalt rakendada – selleks tuleb esmaste andmete korral saadud järeljaotust kasutada uute andmete saamisel eeljaotusena. Intuitiivselt võib sellele mõelda selliselt, et enne uuringu läbiviimist oli meil mingi arvamus uuritava parameetri jaotuse kohta. Pärast esimese komplekti andmete nägemist meie arvamus täpsustus. Teise komplekti andmete kättesaamisel saame seda kasutada kui parimat teavet parameetri jaotuse kohta. Sama mõttekäiku saab korrata iga kord, kui saabub uus komplekt andmeid. Ühtlasi võib sellisele protseduurile mõelda kui õppimisprotsessile, kus uute faktide ilmnemisel uuendame oma teadmisi.
Bayesi lähenemist kasutades on analüüsi tulemuseks uuritava parameetri jaotuse hinnang. Olenevalt olukorrast võib jaotuse raporteerimine olla aga liialt inforohke ja mõnele sihtrühmale ka raskesti mõistetav. Tihtipeale soovitakse tulemuseks „ühte numbrit“: analüüsi kontekstis punkthinnangut. Selle käigus läheb küll kaduma palju teavet, kuid muudab tulemuste esitamise lihtsamaks.
Tüüpilisteks punkthinnanguteks on kas järeljaotuse keskväärtus, mediaan või mood. Teades järeljaotust, on võimalik välja arvutada ka selle muid karakteristikuid, nagu näiteks standardhälvet või kvantiile.
Olgu eesmärgiks hinnata, kui suur osa elanikkonnast toetab praegust valitsust. Selleks küsitakse N isikult, kas ta toetab praegust valitust või mitte. Saadud andmed on seega ![]() kus
kus ![]() , kui i-s vastanu ei toeta valitsust, ja
, kui i-s vastanu ei toeta valitsust, ja ![]() , kui toetab. Tähistagu
, kui toetab. Tähistagu ![]() uuritavat toetusmäära.
uuritavat toetusmäära.
Sagedusstatistikud leiaksid hinnangu toetusmäärale selliselt, et loevad kokku, mitu vastanut on toetaval seisukohal ja jagavad saadud arvu valimimahuga. Kuna ![]() tähistab toetajate arvu, siis
tähistab toetajate arvu, siis ![]()
Bayesi statistikud lahendaksid ülesande aga järgmiselt. Esmalt paneme tähele, et kui valitsuse toetusmäär elanikkonna seas on θ , siis valides ühe juhusliku isiku, on ta tõenäosusega ![]() valitsust toetav. Seega, valides N isikut, on toetajate arv
valitsust toetav. Seega, valides N isikut, on toetajate arv ![]() binoomjaotusega:
binoomjaotusega: ![]() Järelikult andmete tõepärafunktsioon avaldub järgmiselt:
Järelikult andmete tõepärafunktsioon avaldub järgmiselt: ![]() kus
kus ![]() tähistab kombinatsioonide arvu valimaks N isiku seast
tähistab kombinatsioonide arvu valimaks N isiku seast ![]() isikut.
isikut.
Selleks, et saada parameetri ![]() järeljaotust, on veel vaja esmalt ära fikseerida sobiv eeljaotus. Sobiv eeljaotus on nimelt selline, mis on kooskõlas analüüsi läbiviija teadmistega ega lähe vastuollu tõenäosusteooriaga.
järeljaotust, on veel vaja esmalt ära fikseerida sobiv eeljaotus. Sobiv eeljaotus on nimelt selline, mis on kooskõlas analüüsi läbiviija teadmistega ega lähe vastuollu tõenäosusteooriaga.
Valime eeljaotuseks beeta jaotuse. Beeta jaotus on kirjeldatav parameetritega ![]() ja
ja ![]() ning selle tihedusfunktsioon avaldub kujul
ning selle tihedusfunktsioon avaldub kujul 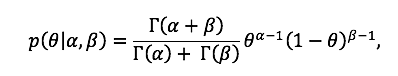 kus
kus ![]() tähistab gamma funktsiooni. Seejuures
tähistab gamma funktsiooni. Seejuures ![]() ja
ja ![]() on hüperparameetrid, st need määratakse analüüsi läbiviija poolt.
on hüperparameetrid, st need määratakse analüüsi läbiviija poolt.
Kuna beeta jaotusest juhuslik väärtus saab omada väärtusi vahemikus 0 kuni 1, siis sobib see tõenäosusteoreetiliselt eeljaotuseks valitsuse toetusmäärale, mis samuti jääb vahemikku 0 kuni 1.
Kasutades Bayesi valemit, leiame toetusmäära järeljaotuse:
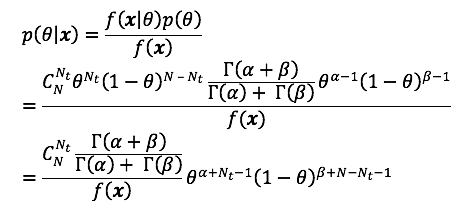
Saadud avaldises on parameetrist ![]() sõltuv osa
sõltuv osa ![]() On näha, et see vastab omakorda beeta jaotusele parameetritega
On näha, et see vastab omakorda beeta jaotusele parameetritega ![]() Lisaks, saadud avaldises olev komponent
Lisaks, saadud avaldises olev komponent
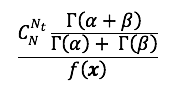 ei sõltu uuritavast parameetrist
ei sõltu uuritavast parameetrist ![]() vaid fikseeritud andmete ja hüperparameetrite korral on tegemist mingi arvuga. Kuna järeljaotuse näol on tegemist tihedusfunktsiooniga, siis ainuvõimalik järeldus on, et
vaid fikseeritud andmete ja hüperparameetrite korral on tegemist mingi arvuga. Kuna järeljaotuse näol on tegemist tihedusfunktsiooniga, siis ainuvõimalik järeldus on, et
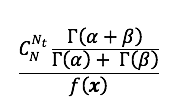 on beeta jaotuse normeerivaks konstandiks, st
on beeta jaotuse normeerivaks konstandiks, st
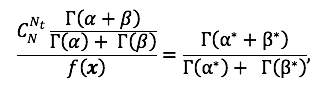 ja järeljaotuseks on beeta jaotus parameetritega
ja järeljaotuseks on beeta jaotus parameetritega ![]() ja
ja ![]()
Asjaolu, et järeljaotus on samast jaotusklassist nagu eeljaotus, annab suure arvutusliku eelise. Antud näite korral tuleb järeljaotuse leidmiseks vaid vastavalt valemile uuendada eeljaotuse parameetreid. Seejuures saame täpselt sama lähenemist kasutada täiendavate andmete laekumisel. Sellist jaotust, mille korral nii eel- kui ka järeljaotus on samast klassist, nimetatakse vaatlusandmete jaotuse kaasjaotuseks (conjugate prior). Antud näitest on näha, et binoomjaotusega vaatluste kaasjaotuseks on beeta jaotus.
Kokkuvõtvalt, eeldades eeljaotusena beeta jaotust, saame valitsuse toetusmäära järeljaotuse arvutamiseks järgmise eeskirja:
1. Fikseeri eeljaotuse ![]() ja
ja ![]() ,
,
2. Arvuta ![]() st leia valitsust toetavate isikute arv valimis,
st leia valitsust toetavate isikute arv valimis,
3. Järeljaotuse parameetrite leidmiseks arvuta:
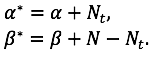
Vaatame lähemalt nelja näiteolukorda, kus igal juhul on küsitletud 10 inimest (N=10), kuid varieerime eeljaotuse parameetreid ja valitsust toetavate isikute arvu.
Näide 1. Uudistest loetu ja sisetunde põhjal arvab uuringu läbiviija, et valitsuse toetusmäär on pigem madal – võimalik, et keskmiselt umbkaudu 1 vastaja 6-st on toetaval seisukohal. Teisisõnu võiks oodatav toetusmäär tema hinnangul olla keskmiselt 1/6. Kuna parameetritega ![]() ja
ja ![]() määratud beeta jaotuse keskväärtus on
määratud beeta jaotuse keskväärtus on ![]() siis kaalub ta hüperparameetrite väärtustena kasutada väärtusi
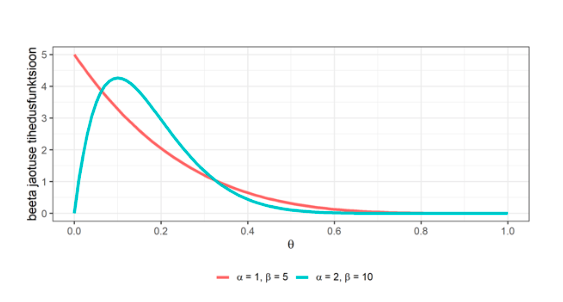
siis kaalub ta hüperparameetrite väärtustena kasutada väärtusi ![]() Joonistades välja vastava beeta jaotuse tihedusfunktsiooni, näeb ta, et selliste parameetrite korral on liialt suur võimalus saada nullile väga lähedasi väärtusi (joonis 1) ning kuigi arvatavasti on toetusmäär pigem madal, on valitsusel siiski oma toetajaskond kindlasti olemas. Kuna eelnevalt fikseeritud hüperparameetrite väärtused ei sobi tema eelteadmistega, otsustab uuringu läbiviija järgmisena proovida väärtusi
Joonistades välja vastava beeta jaotuse tihedusfunktsiooni, näeb ta, et selliste parameetrite korral on liialt suur võimalus saada nullile väga lähedasi väärtusi (joonis 1) ning kuigi arvatavasti on toetusmäär pigem madal, on valitsusel siiski oma toetajaskond kindlasti olemas. Kuna eelnevalt fikseeritud hüperparameetrite väärtused ei sobi tema eelteadmistega, otsustab uuringu läbiviija järgmisena proovida väärtusi ![]() Ka sel juhul on keskväärtus samuti 1/6, kuid nüüd saadav tihedusfunktsiooni kuju sobib tema eelteadmistega paremini (joonis 1). Olles kaalunud ka mõningaid teisi
Ka sel juhul on keskväärtus samuti 1/6, kuid nüüd saadav tihedusfunktsiooni kuju sobib tema eelteadmistega paremini (joonis 1). Olles kaalunud ka mõningaid teisi ![]() ja
ja ![]() väärtusi, otsustab ta siiski jääda algväärtuste
väärtusi, otsustab ta siiski jääda algväärtuste ![]() juurde.
juurde.
Olles formuleerinud oma eelteadmised, asub analüütik läbi viima küsitlust. Selleks küsitleb ta 10 juhuslikult valitud isikut, kellest 6 on valitsust toetaval seisukohal ![]()
Viimase sammuna tuleb veel arvutada järeljaotuse parameetrid: ![]() . Raporteerides punkthinnanguna järeljaotuse keskväärtust, on valitsuse toetusmäära hinnanguks
. Raporteerides punkthinnanguna järeljaotuse keskväärtust, on valitsuse toetusmäära hinnanguks ![]()
Näide 2. Teisel analüütikul on kavas viia läbi samasugune uuring nagu näites 1. Sel korral on uuringu läbiviija aga ise valitsust toetav ning kõik tema peamised tuttavad on samasugusel seisukohal. Selline kajakambris viibimine on temas tekitanud arvamuse, et valitsuse toetusmäär ühiskonnas ongi üsna kõrge. Sellest tulenevalt valib ta hüperparameetriteks ![]() st tema ootuste kohaselt võiks 12 isikust 10 olla valitsust toetavad. Viies läbi küsitluse ning saades tulemuseks, et 10 vastajast 6 toetab praegust valitsust, uuendab analüütik oma teadmisi vastavalt arvutusalgoritmile:
st tema ootuste kohaselt võiks 12 isikust 10 olla valitsust toetavad. Viies läbi küsitluse ning saades tulemuseks, et 10 vastajast 6 toetab praegust valitsust, uuendab analüütik oma teadmisi vastavalt arvutusalgoritmile: ![]() Toetusmäära punkthinnanguks on seega
Toetusmäära punkthinnanguks on seega ![]()
Näidete 1 ja 2 põhjal on näha, et sõltuvalt eelteadmistest võivad analüüsi tulemused isegi samade andmete korral tugevalt erineda. Kuigi teatud juhtudel võimaldab olemasolevate teadmiste kasutuselevõtt vähemalt teoreetiliselt täpsemaid tulemusi saada, toob see paratamatult sisse ka subjektiivsuse komponendi. Subjektiivsus on aga tegur, mida teaduslikus uuringus võimalikult suurel määral vältida tuleb. Tugineda tuleb faktidele, milleks on eelkõige andmed.
Õnneks on Bayesi analüüsis subjektiivsuse vältimiseks olemas sobiv lahendus: eeljaotuse hüperparameetriteks tuleb valida sellised väärtused, mille korral kõikvõimalikud uuritava parameetri väärtused on eelteadmiste järgi võrdvõimalikud. Selliselt määratud eeljaotust nimetatakse mitteinformatiivseks eeljaotuseks (non-informative prior). Kasutades mitteinformatiivset eeljaotust, on tulemused kas samad või vähemasti lähedased klassikalise statistika meetoditega saadud tulemustele.
Näiteks, kui beeta jaotuse korral valida hüperparameetriteks ![]() , saame vahemikule 0 kuni 1 vastava ühtlase jaotuse. Kui aga mingi uuritava parameetri
, saame vahemikule 0 kuni 1 vastava ühtlase jaotuse. Kui aga mingi uuritava parameetri ![]() eeljaotuseks on valitud normaaljaotus hüperparameetritega
eeljaotuseks on valitud normaaljaotus hüperparameetritega ![]() siis oma ebakindluse väljendamiseks ning subjektiivsuse vähendamiseks saab suurendada hajuvusparameetrit
siis oma ebakindluse väljendamiseks ning subjektiivsuse vähendamiseks saab suurendada hajuvusparameetrit ![]()
Näide 3. Viime läbi näidetes 1 ja 2 esitatud uuringu, kuid kasutame sel korral mitteinformatiivset eeljaotust. Fikseerime seega ![]() Eeljaotuse kohaselt on oodatav toetusmäär
Eeljaotuse kohaselt on oodatav toetusmäär ![]() Kuna andmete põhjal
Kuna andmete põhjal ![]() siis järeljaotuse parameetrid on
siis järeljaotuse parameetrid on ![]() millest omakorda saame, et
millest omakorda saame, et ![]() Näeme, et saadud hinnang ei kattu küll täielikult klassikalise statistika hinnanguga, milleks on
Näeme, et saadud hinnang ei kattu küll täielikult klassikalise statistika hinnanguga, milleks on 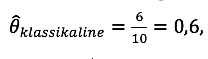 kuid on sellele võrdlemisi lähedal.
kuid on sellele võrdlemisi lähedal.
Näide 4. Vaatleme nüüd aga olukorda, kui 10 küsitletust mitte ükski pole valitsust toetaval seisukohal, st ![]() On selge, et klassikalise statistikaga saaksime toetuse hinnanguks
On selge, et klassikalise statistikaga saaksime toetuse hinnanguks ![]() Kuna valimi maht on väga väike, on täiesti reaalne saada selline valim, kus kõik on „vastu“. Küll aga on raske aktsepteerida hinnangut, et kogu ühiskonnas võiks toetusmäär 0 olla. Bayesi analüüsi tulemused on seevastu mõnevõrra paindlikumad: valides eeljaotuseks mitteinformatiivse beeta jaotuse (st
Kuna valimi maht on väga väike, on täiesti reaalne saada selline valim, kus kõik on „vastu“. Küll aga on raske aktsepteerida hinnangut, et kogu ühiskonnas võiks toetusmäär 0 olla. Bayesi analüüsi tulemused on seevastu mõnevõrra paindlikumad: valides eeljaotuseks mitteinformatiivse beeta jaotuse (st ![]() ), saame, et
), saame, et 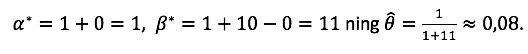
Nagu just veenduda võisime, sobib Bayesi statistikat kasutada harva esinevate sündmuste korral.
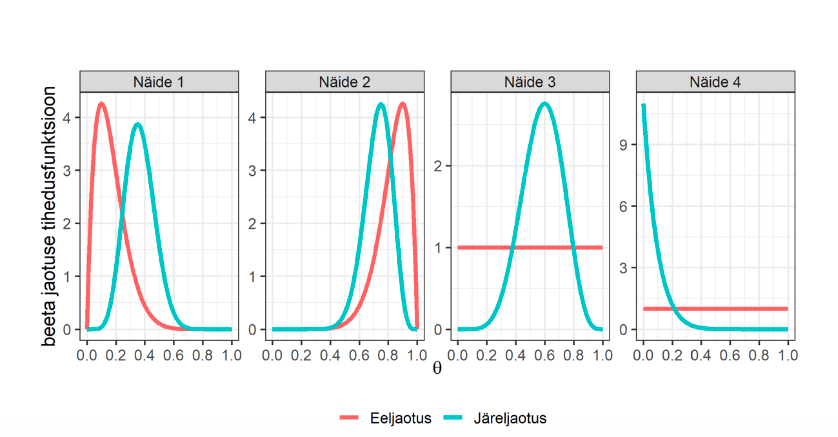
Joonis 2 aitab visualiseerida, kuidas näidetes 1 kuni 4 fikseeritud eeljaotustest ja saadud andmetest sõltuvalt kujuneb järeljaotus. Näidetes 1 kuni 3 on olnud kasutada samad andmed, kuid sõltuvalt eeljaotuse valikust on järeljaotused ja sellest tuletatavad tulemused võrdlemisi erinevad. Näiteid 3 ja 4 võrreldes on aga näha, kuidas sama (mitteinformatiivse) eeljaotuse korral on erinevus andmetes tinginud tugevad erinevused järeljaotuses.
Näidetes 1 kuni 4 olev sisu on kokku koondatud tabelis 1.
Tabel 1. Näidetes 1 kuni 4 leitud punkthinnangute võrdlus N = 10 korral
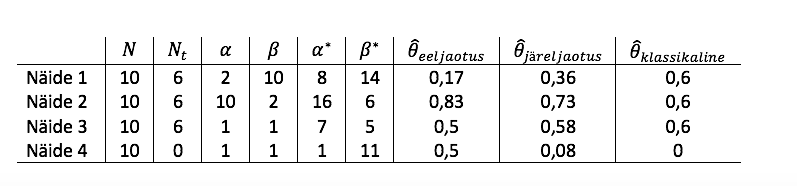
On selge, et valim mahuga 10 on väga väike. Mis toimub aga valimi mahu kasvades? Intuitiivselt võiks oodata, et mida enam on andmeid (st mida kõnekamad on faktid), seda tugevamalt võtame neid arvesse oma järelduste tegemisel. Teisisõnu võiks eelteadmiste osatähtsus täiendavate faktide ilmnemisel aina väheneda. Osutub, et Bayesi statistikas see nii ka on.
Vaatleme näidetes 1 kuni 4 esitatud olukordi, kuid võtame nüüd valimi mahuks ![]() jättes valitsust toetavate isikute valimisisese proportsiooni samaks, st näidetes 1 kuni 3
jättes valitsust toetavate isikute valimisisese proportsiooni samaks, st näidetes 1 kuni 3 ![]() ja näites 4
ja näites 4 ![]() . Jooniselt 3 on näha, kuidas toetusmäära
. Jooniselt 3 on näha, kuidas toetusmäära ![]() järeljaotus on tugevalt kontsentreeritud valimisisese proportsiooni ümbrusesse, ning kuigi näidetes 1 kuni 3 esitatud eeljaotused on täiesti erinevad, siis järeljaotused on visuaalselt väga sarnased.
järeljaotus on tugevalt kontsentreeritud valimisisese proportsiooni ümbrusesse, ning kuigi näidetes 1 kuni 3 esitatud eeljaotused on täiesti erinevad, siis järeljaotused on visuaalselt väga sarnased.
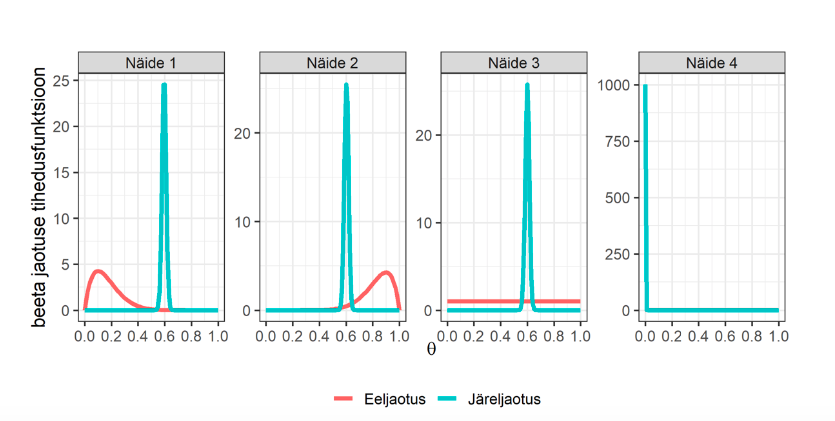
Ühtlasi saame tabeli 2 põhjal veenduda, et Bayesi statistika põhjal leitud punkthinnangud (![]() ) on juba väga lähedased klassikalise statistika hinnangutele.
) on juba väga lähedased klassikalise statistika hinnangutele.
Tabel 2. Näidetes 1 kuni 4 leitud punkthinnangute võrdlus N = 1000 korral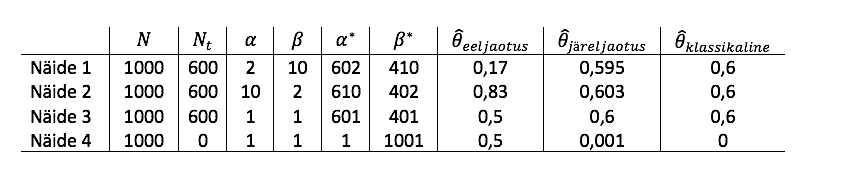
Sagedusstatistikud kasutavad uuritava parameetri punkthinnangu usaldusväärsuse kirjeldamiseks usaldusvahemikku. Klassikalise statistika eelduse kohaselt on uuritav parameeter fikseeritud ning juhuslik on vaid saadav valim. Seega on juhuslik ka valimi põhjal arvutatav usaldusvahemik, mistõttu on väär näiteks 95% usaldusvahemikku tõlgendada selliselt, et tõenäosusega 95% kuulub tegelik üldkogumi parameeter leitud vahemikku. Kuna nii leitud usaldusvahemik kui ka tegelik parameeter on fikseeritud, siis tegelik parameeter kas kuulub või ei kuulu leitud vahemikku, st tõenäosus, et üldkogumi parameeter kuulub leitud vahemikku, on vastavalt kas 1 või 0. Korrektne 95% usaldusvahemiku tõlgendus on hoopis selline: kui korrata valimi võtmise protsessi ja iga valimi korral arvutada 95% usaldusvahemik, siis oodatavalt 95% juhtudest jääb tegelik parameeter leitud vahemikku.
Bayesi statistikud kasutavad usaldusvahemiku asemel tõenäosusvahemikku (probability interval, credibility interval). Kuna Bayesi statistika lähtub eeldusest, et üldkogumi parameeter on juhuslik suurus, siis saame rääkida tõenäosusest, et see kuulub mingisse etteantud vahemikku. Näiteks parameetri ![]() tõenäosusvahemik
tõenäosusvahemik ![]() defineeritakse kui
defineeritakse kui ![]() Seega on tõenäosusvahemiku tõlgendamine tunduvalt intuitiivsem kui usaldusvahemiku tõlgendamine: näiteks 95% tõenäosusvahemiku korral on tõlgenduseks „tõenäosusega 95% kuulub üldkogumi parameeter vahemikku
Seega on tõenäosusvahemiku tõlgendamine tunduvalt intuitiivsem kui usaldusvahemiku tõlgendamine: näiteks 95% tõenäosusvahemiku korral on tõlgenduseks „tõenäosusega 95% kuulub üldkogumi parameeter vahemikku ![]() .
.
Tõenäosusvahemiku leidmiseks tuleb pöörata tähelepanu asjaolule, et see ei ole üldiselt üheselt määratud. Näiteks sobivad 95% tõenäosusvahemikuks nii ( ![]() ) kui ka (
) kui ka (![]() ), kus
), kus ![]() ja
ja ![]() on vastavalt uuritava parameetri
on vastavalt uuritava parameetri ![]() järeljaotuse 0,95 ja 0,05 kvantiilid. Üldiselt on siiski mõistlik valida võimalikest tõenäosusvahemikest kõige lühema pikkusega vahemik või selline vahemik, mille saamiseks on jaotuse mõlemast sabast ära visatud sama suur tõenäosusmass: kui on teada järeljaotuse analüütiline kuju, saab leida 0,025 ja 0,975 kvantiilid
järeljaotuse 0,95 ja 0,05 kvantiilid. Üldiselt on siiski mõistlik valida võimalikest tõenäosusvahemikest kõige lühema pikkusega vahemik või selline vahemik, mille saamiseks on jaotuse mõlemast sabast ära visatud sama suur tõenäosusmass: kui on teada järeljaotuse analüütiline kuju, saab leida 0,025 ja 0,975 kvantiilid ![]() ja
ja ![]() ning nendest konstrueeritud vahemik (
ning nendest konstrueeritud vahemik (![]() ) ongi soovitud 95% tõenäosusvahemik. Kui analüütiliselt ei õnnestu soovitud kvantiile arvutada, on neid võimalik hinnata järeljaotusest simuleerimise teel. Selleks tuleb järeljaotuse põhjal genereerida
) ongi soovitud 95% tõenäosusvahemik. Kui analüütiliselt ei õnnestu soovitud kvantiile arvutada, on neid võimalik hinnata järeljaotusest simuleerimise teel. Selleks tuleb järeljaotuse põhjal genereerida ![]() võimalikku realisatsiooni ning järjestada need kasvavalt. Kvantiili
võimalikku realisatsiooni ning järjestada need kasvavalt. Kvantiili ![]() hinnanguks on positsioonil
hinnanguks on positsioonil ![]() asuv element (seda juhul, kui
asuv element (seda juhul, kui ![]() on täisarv, vastasel juhul tuleb tõenäosusvahemiku vasaku otspunkti leidmiseks suurust
on täisarv, vastasel juhul tuleb tõenäosusvahemiku vasaku otspunkti leidmiseks suurust ![]() ümardada lähima täisarvuni allapoole ja parema otspunkti leidmiseks ümardada lähima täisarvuni ülespoole). Näites
ümardada lähima täisarvuni allapoole ja parema otspunkti leidmiseks ümardada lähima täisarvuni ülespoole). Näites ![]() korral tuleb 95% tõenäosusvahemiku leidmiseks valida kasvavalt järjestatud simuleeritud väärtustest positsioonidel
korral tuleb 95% tõenäosusvahemiku leidmiseks valida kasvavalt järjestatud simuleeritud väärtustest positsioonidel ![]() ja
ja ![]() asuvad väärtused.
asuvad väärtused.
Tihtipeale ei ole järeljaotust võimalik analüütiliselt leida. Sel juhul tuleb kasutada simuleerimist. Levinud lühendiks on MCMC (Markov Chain Monte Carlo), mis kujutab endast Markovi ahelatel põhinevaid simuleerimismeetodeid. Nendest algoritmidest ülevaate saamiseks on soovitatav tutvuda näiteks alloleva kirjandusega.
Clyde, M. et al. (2019). An Introduction to Bayesian Thinking. Kättesaadav internetist aadressil https://statswithr.github.io/book/.
Koch, K.-R. (2007). Introduction to Bayesian Statistics. Berlin, Heidelberg: Springer.
Lync, S. M. (2007). Introduction to Applied Bayesian Statistics and Estimation for Social Scientists. New York: Springer.
J. Esarey videokursus: https://www.youtube.com/playlist?list=PLAFC5F02F224FA59F
Valminud Hariduse Infotehnoloogia Sihtasutuse IT Akadeemia programmi toel.


