Andmeanalüüsi tüüpiline ülesanne on avaldada sõltuva tunnuse Y variatiivsus teatud sõltumatute tunnuste X₁, X₂, …, X_M kaudu lineaarse mudeli kohaselt:

kus e on mudeli statistiline viga, mille kohta klassikalisel juhul eeldatakse jaotumist normaaljaotuse kohaselt keskmisega 0, ühetaolist hajuvust ja teatud sõltumatuse tingimusi. Püüame seda mõtet selgitada lihtsa erijuhu varal.

Olgu seletavaid tunnuseid üks (M = 1) ja see olgu kaheväärtuseline väärtustega x₁ ja x₂, määrates kaks gruppi. Siis keskmiselt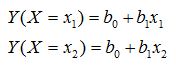

Võtame tunnuseks X indikaatortunnuse I, mis annab täielikult edasi tunnuse X informatsiooni:

I = 1, kui indiviidi väärtuseks tunnusel X on x₁

I = 0, kui indiviidi väärtuseks tunnusel X on x₂

Saame regressioonivõrrandi

Kui tunnuse X väärtuseks on x₁, siis prognostiline  tunnuse Y väärtus on b₀ + b₁. Kui tunnuse X väärtuseks on x₂, siis prognostiline tunnuse Y väärtus on b₀.  Gruppe määrava tunnuse X seisukohalt on sõltuva tunnuse Y keskmiste erinevuseks kahe grupi vahel b₁ ehk regressioonikordaja väärtus.

Kui seletaval tunnusel on enam kui kaks väärtust (tunnus eristab üksteisest enam kui kaht gruppi), siis saame analoogilise mõttekäigu, kui lülitame mudelisse k–1 grupiindikaatorit, kus k on gruppide arv. Näiteks piirkonna tunnuse, millel on viis väärtust (Põhja-Eesti, Lääne-Eesti, Kesk-Eesti, Kirde-Eesti, Lõuna-Eesti) saame edasi anda järgmise nelja indikaatori varal:

I_Põhja-Eesti   = 1, kui elukohaks on Põhja-Eesti, ja I_Põhja-Eesti = 0 ülejäänud indiviididel;

I_{Lääne-Eesti}  = 1, kui elukohaks on Lääne-Eesti, ja I_{Lääne-Eesti} = 0 ülejäänud indiviididel;

I_Kesk-Eesti   = 1, kui elukohaks on Kesk-Eesti, ja I_Kesk-Eesti = 0 ülejäänud indiviididel;

I_Kirde-Eesti   = 1, kui elukohaks on Kirde-Eesti, ja I_Kirde-Eesti = 0 ülejäänud indiviididel.

Lõuna-Eesti elanikud tunneme ära selle järgi, et kõigi nelja indikaatortunnuse väärtuseks on 0. Kasutusel on teisigi ümberkodeerimise viise.

Regressioonimudel esitub praegusel juhul kujul:

Mudelipärased prognoositud keskmised on viies piirkonnas järgmised:

Kui sõltuva tunnuse keskmine oleks kõigis piirkondades üks ja sama, siis kehtiks:

b₁ = b₂ = b₃ = b₄ = 0. Kui keskmine ei ole üks ja sama, siis vähemalt üks regressioonikordaja, kas b₁, b₂, b₃ või b₄, erineb nullist.

Kasutatavatele tunnustele omistatakse analüüsis kindel roll:            

1. faktorid  (argumenttunnused, sõltumatud tunnused), mis määravad liigenduse keskmise poolest uuritavateks gruppideks;
2. sõltuv tunnus (funktsioontunnus), mille keskmist uuritakse faktorite mõju seisukohalt.

Kui argumenttunnuseid on üks, siis on tegemist ühefaktorilise dispersioonanalüüsi mudeliga (ingl One-way ANOVA , ANOVA – Analysis of Variance). Kui faktoreid on mitu, siis kõneleme kahe-, kolme- jne ehk mitmefaktorilisest dispersioonanalüüsist (ingl Two-way ANOVA jne). Kui funktsioontunnuseid on vaatluse all korraga mitu, siis räägitakse mitmemõõtmelisest dispersioonanalüüsist (ingl Multivariate analysis of Variance, MANOVA). Mitmemõõtmelise dispersioonanalüüsi sisemise loogika kohaselt peegeldavad sõltuvad tunnused uuritava objekti teatavat ühist omadust või omavahel seotud omadusi, mille alusel on võimalik vaadeldavaid gruppe üksteisest keskmiselt eristada.

Faktorid peavad olema kategoriaalsed: kas olemuselt diskreetne või klassifitseeritud skaala sisuliselt selgelt eristuvate gruppidega. Nt pideva tunnuse klassifitseerimisel saadud grupitunnus ei ole naabergruppide poolest alati selgelt eristav. Faktori kategooriaid nimetatakse ka faktori tasemeteks. Sõltuv tunnus peab olema mõõdetud vahemik- või suhteskaalal (arvuline tunnus, pidev skaala) ja olenevalt mudelist lisatakse täiendavaid eeldusi, millest tuleb juttu edaspidi.

Sõnastame nendes mõistetes dispersioonanalüüsi mõtte: uuritakse, kui tõepäraselt võib kinnitada erinevusi sõltuva tunnuse keskmistes faktori eri tasemetel. Kui küllalt tõepäraselt, siis räägitakse faktori (tasemeid määrava tunnuse) diferentseerivast mõjust sõltuvale tunnusele. Dispersioonanalüüs ei anna vastust küsimusele, milles erinevus seisneb. Seda tuleb eraldi täpsustada (nt nn post hoc-testid tasemerühmade paarikaupa võrdlemiseks). Kui saame meie näites teada, et töö iseloomust sõltuvalt on töörahulolus erisusi, siis on loomulik välja selgitada ülesande lõplikuks lahendamiseks keskmiste mitmese paarikaupa võrdluse teel, kas keskmisi erinevusi ilmneb nt füüsilise objektiga töötavate isikute ja paberitöö tegijate rahulolus või mõnes teises suhtes.

Võtmeküsimuseks on sõltuva tunnuse hälvete (variatiivsuse) analüüs, kusjuures hälbeid vaadeldakse mitme eri püsipunkti suhtes, milleks on erisuguse tähendusega keskmised. Tõepoolest, võime kõnelda meie näite korral üldkeskmisest rahulolu tasemest ja individuaalsetest hälvetest selle suhtes (koguhajuvus). Samal ajal võiks kõnelda individuaalsetest hälvetest sama iseloomuga tööd tegevate inimeste grupi sisese keskmise rahulolu suhtes (gruppidesisene hajuvus). Veel võiks vaadelda, kuidas erisuguse töö iseloomuga üksikgruppide keskmine rahulolu erineb üldkeskmisest rahulolust.

Lähedase väärtusega rühmakeskmiste korral väljendavad hälbed üksnes individuaalset muutlikkust. Erisuguste  keskmiste korral seevastu liitub hälvetes individuaalne ja tasemegruppide vaheline muutlikkus. Seega taandub keskmiste võrdluse ülesanne hajuvuse komponentide eritlemiseks ehk analüüsiks, millest tuleneb  ka meetodi nimetus — dispersioonanalüüs.

Vaatleme esmalt ülesannet, kus sõltuva tunnuse keskmist variatiivsust uuritakse ühe liigendava faktori seisukohalt. Ühefaktoriline mudel keskmise kohta (populatsioonis ehk üldkogumis) kehtestatakse kujul:

m_i  = m + a_i ,

kus m _i on sõltuva tunnuse keskmine faktori taseme i korral, a_i  on faktori tasemele i vastav komponent ja m on kõigile tasemeile ühine konstant, i = 1, 2, …, k, k – faktori tasemete arv. Statistiliseks hüpoteesiks on: iga i korral a_i = 0 ehk kõigis tasemegruppides on sõltuva tunnuse keskmine üks ja sama, nimelt m. Kui see hüpotees kummutatakse, siis kõneldakse tasemete keskmiste erinevustest ja faktori usaldusväärsest mõjust sõltuvale tunnusele. Mudel kehtestatakse niisiis faktori tasemegruppide kaupa.

Individuaalsete väärtuste kohta tasemel i kehtib mudel ligikaudu:

x(j) = m + a_i + e(j) ,

kus lisatud osa e(j) on tasemele i kuuluva indiviidi j puhul mudeli viga. Vigade jaotus eeldatakse tasemerühmades olevat ühesuguse dispersiooniga, sageli nõutakse normaaljaotust. Viga eeldatakse keskmiselt olevat null. Suhteliselt lihtsa teoreetilise ja tehnilise käsitluse pakub tasakaalustatud mudel, mil tasemed on esindatud ühesuuruste indiviidirühmade kaudu. Selle käsitluse kohaseid valemeid püüamegi DA idee seletamiseks allpool kasutada.

Nagu eespool juba öeldud, on dispersioonanalüüsi puhul olulisel kohal sõltuva tunnuse varieeruvus hälvete kujul. Allpool oleval skeemil on kujutatud sõltuva tunnuse teljel üht konkreetset indiviidi j (punane ruut), kes pärineb faktori tasemelt i ja kellel on sõltuva tunnuse väärtuseks y_ij.  Individuaalse hälbe sõltuva tunnuse üldkeskmisest m (suurem sinine ring) saab esitada kahes osas – hälbena tasemekeskmisest m_j (väiksem sinine ring) ja tasemekeskmise hälbena üldkeskmisest:

kus i = 1, 2, …, k ja k on faktori tasemete arv. Skeemil on vastavad lõigud sama värvi nagu valemis.

Selgitame näite varal põhjalikumalt, mida need värvilised hälbed tähendavad. Uurime Euroopa sotsiaaluuringu 2010. aasta andmeil seda, kuidas oleneb eluga üldine rahulolu sellest, millistel ajenditel pingutatakse igapäevase töö juures. Tunnuste tähenduse ja andmetega on võimalik tutvuda aadressilt http://www.yti.ut.ee/et/euroopa-sotsiaaluuring lähtudes. Sõltuvat tunnust – eluga üldist rahulolu – mõõdeti skaalal 0 (täielikult rahulolematu) kuni 10 (täielikult rahul). Andmed on 732 töötaja kohta. Faktorit (peamine põhjus töö juures pingutamiseks) vaadeldi kuuel tasemel (vt tabel 1, „muu“ jäi kõrvale). Eluga rahulolu tasemekeskmised varieeruvad vahemikus 5,9 kuni 7,2 punkti. Tasemesisene hajuvus standardhälbe alusel on eri põhjuste korral 1,9 kuni 2,2 punkti.

Millistest hälvetest käib jutt? Oletame,  et vastaja, kes teeb tööpingutusi seepärast, et tema tööülesanded on huvitavad, hindas üldist eluga rahulolu 7 punktiga. Tema hinnang on 0,19 = 7,19 − 7 punkti võrra madalam kui teistel sama töömotiiviga inimestel (vt tabel 1, vaadelge värve äsjasel skeemil) ja 7 − 6,65 = 0,35 punkti  võrra kõrgem üldkeskmisest. Sellise pingutamise põhjusega vastajate keskmine eluga rahulolu hinnang on 7,19 − 6,65 = 0,54 punkti võrra kõrgem kui üldkeskmine hinnang.

Jätkame hälvete mõttega ja püüame ühe indiviidi hälvete asemel võtta kokku kõigi indiviidide hälbed. Lihtne kokkuliitmine annaks tulemuseks nulli (hälbed on leitud ju keskmiste suhtes). Et variatiivsuse kokkuvõtmisel ei ole esmatähtis hälbe märk, vaid esmatähtis on variatiivsuse ulatus, siis vaadeldakse ruuthälbeid. Liites kokku ruutu võetud hälbed eelmise osa „värvilises valemis“, saame summaarse ruuthälbe järgmise lahutuse (eeldatakse, et tasemerühmad on ühe ja sama suurusega n indiviidi ehk meil on tasakaalus katseplaan):

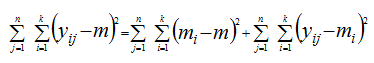
Traditsioonilises tähistuses kasutatakse ingliskeelseid sõnu:

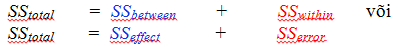
Osade tähendus selles lahutuses on järgmine:

koguhälve (SS_total) =
rühmadevahelistest erinevustest tingitud hälve (SS_between) +
rühmadesisesest juhuslikust hajuvusest tingitud hälve (SS_within).

Rühmadesisest hajuvuse osa (SS_within) võiks nimetada ka veel veaks, jääkhajuvuseks (ingl error, residual). Summaarne ruuthälve oleneb loomulikult sellest, kui palju liikmeid liidetakse. Et sellisest mõjust vabaneda, vaadeldakse ruuthälvete üldisuse suurendamiseks summaarset ruuthälvet vabadusastmete arvu kohta (df, kohe selgitame, mida vabadusaste tähendab):

            MS_total   = SS_total : df_total = SS_total : (nk − 1)

            MS_between= SS_between : df_between = SS_between : (k − 1)

            MS_within    = SS_within : df_within = SS_within : (nk − k)

Kuidas määratakse vabadusastmete arv? Üldreegel vabadusastmete arvu määramiseks on „kasutada olevate infoühikute arv miinus kitsenduste (seoste) arv“.

Koguhajuvus määratakse meie vaadeldud tasakaalustatud mudelis nk mõõtmise alusel (igal tasemel mõõdeti n indiviidi andmed, tasemeid on k), millest üks vabadusaste „kulub“ fikseeritud üldkeskmise jaoks, st vabadusastmete arv on nk − 1. Rühmadesisene dispersioon määratakse kõigi tasemete peale kokku, arvestades igal tasemel oma keskmist.  Igal tasemel on üks vabadusaste vähem kui indiviidide arv n sellel tasemel, sest tasemekeskmine on fikseeritud (kitsendus), ja k tasemel kokku  on k(n − 1) vabadusastet. Rühmadevahelise hajuvuse määramisel on „infoühikuteks“ k tasemekeskmist. Et hälbeid vaadeldakse andmestiku kindla üldkeskmise suhtes (kitsendus), siis tuleb vabadusastmete arvuks k − 1. Kokku saame võrduse: nk − 1 =   = k(n − 1) + k − 1.

Meie näites on vabadusastmete arvudeks ülaltoodud järjekorras 732 − 1 = 731, 731 − (6 − 1) = 725 ja 6 − 1 = 5. Loodame, et hilisemas arvutiväljundis leiab äsjane arutlus kinnitust.

Tuletame meelde, mis on meie uurimise eesmärgiks — hinnata tasemekeskmiste sarnasuse tõepärasust ja teha seda hajuvuse osadele tuginedes. Kui tasemekeskmiste hälbed üldkeskmisest on suured (sinine osa valemis), siis ongi alust arvata erinevusi tasemekeskmistes. Et tunnusele on iseloomulik teatav oma variatiivsuse määr, siis ei saa niisama lihtsalt öelda, milline on suur ja milline väike variatiivsus. Erinevust faktori tasemete vahel peegeldatakse hajuvuskomponentide suhte varal, vaadeldes tasemetevahelist hajuvust jääkhajuvuse taustal (sinine osa jagada punasega). Dispersioonanalüüsi idee selgitamiseks võiks huviline lugeja vaadelda ka simulatsiooni aadressil http://www.ruf.rice.edu/~lane/stat_sim/one-way .

Fisher tõestas, et faktori mõju puudumisel keskmistele (nullhüpotees) on tasemetevahelise hajuvuse suhe jääkhajuvusse (avaldatuna ruutkeskmiste hälvete kaudu)

                                                F = MS_between : MS_within

ligikaudu F-jaotusega vabadusastmete arvudega k − 1 ja k(n − 1). Mida suurem on faktori poolt määratud tasemete keskmiste erinevus, seda suurem tuleb F-suhe (ühtede ja samade vabadusastmete arvude juures). Seega võib F-suhte väärtus võrreldavates olukordades olla sisuliselt oluline parameeter. Kui faktoril on kaks taset, siis ühtib vastava t-testi tulemus dispersioonanalüüsi tulemusega, kusjuures t² = F (vt võrdlusülesanded). Seega ei ole mingit vajadust kahetasemelise faktori puhul rakendada ühefaktorilist dispersioonanalüüsi, vaid täpselt sama tähendusega tulemuse saab kätte t-testiga, sealjuures palju lihtsama mõttekäigu alusel.

Teine oluline parameeter F-suhte kõrval on dispersioonimudeli kirjeldusaste (traditsiooniline tähistus R², analoogia regressioonimudeliga, vt regressioonanalüüs):

                                                R² = SS_between : SS_total

Kirjeldusaste väljendab seda osa sõltuva tunnuse dispersioonist, mida saab  „ennustada“, teades indiviidi grupikuuluvust faktori poolest.

Jätkame näidet eluga üldise rahulolu seotusest töökohal panustamise põhjustega. Joonisel 1

on kujutatud keskmine eluga rahulolu koos usaldusvahemikega usaldusnivool 95%. Näeme erisugust keskmist rahulolutaset erisuguse motivatsiooni korral, kuid lahtiseks jääb küsimus, kas need palja silmaga märgatavad erisused on ka üle kantavad teatava statistilise seaduspärana populatsioonile tervikuna. Märkame, et valikuga „oma töökoha säilitamiseks“ kaasneb kõige madalam keskmine ja sealjuures ei lõiku selle keskmise usaldusvahemik peaaegu mitte ühegi teise usaldusvahemikuga. Selle põhjuse korral on eluga üldine rahulolu keskmiselt kõige madalam ja seda kõrge statistilise usaldusväärsusega. Ülejäänud põhjuste gruppides on näha usaldusvahemike kattuvust.

Et gruppide suurus on 100–150 indiviidi ringis, siis viitab usaldusvahemike sarnane laius eluga rahulolu hinnangute küllaltki ühetaolisele hajuvusastmele gruppide sees.

Tabelis 2 on esitatud eluga üldise rahulolu dispersioonitabel töösse panustamise põhjuse kui faktori suhtes. Koguhajuvus summaarse ruuthälbe kujul on 3242, millest faktori (tunnuse lühinimi mnrsefw) tasemetevahelistest erinevustest tingitud osa on 142 ehk 4,4%. Jääkhajuvus (individuaalsed eripärad, kontrolli alla võtmata faktorite mõju) on 3100. Ruutkeskmine hajuvus faktori ühe taseme kohta (õigemini, tasemete arv miinus 1 kohta) on 28,4, jääkhajuvus ligikaudu ühe indiviidi kohta 4,3. Nende kahe suhe ehk F-suhe on praegu 6,7. Seda arvu saab kasutada hüpoteesi „faktori mõju puudub“ kontrollimiseks,  toetudes  F-jaotuse läveväärtustele vabadusastmete arvude 5 ja 726 korral (df – lühend, ingl number of degrees of freedom). Et F-jaotus ei ole lihtsa iseloomuga ja otsustada, kas 6,7 on või ei ole kooskõlas vastava teoreetilise F-jaotusega, ei ole niisama lihtne, siis vaatleme praegu pigem meile osutatud olulisuse tõenäosust, mis on alla 0,0005 ehk väga väike. Seega tuleb hüpotees kummutada ja saaksime kinnitada erisusi rahulolus olenevalt töö juures pingutamise põhjustest. Osa rahulolu variatiivsusest, mille „kirjeldab ära“ faktori rühmakuuluvuse teadmine, on üsna tagasihoidlik – 4,4%. Seega selgus kõrgelt statistiliselt usaldusväärne, aga nõrk faktori mõju.

Milles seisneb tasemetevaheline erinevus? Teatava ettekujutuse sellest andis juba keskmiste graafik koos usaldusvahemikega. Tabelis 3 võib jälgida keskmise mõjukomponente ehk osakesi, milleks saab keskmise lahutada olenevalt eluga rahulolu variatiivsuse allikast. Kasutame viit indikaatortunnust kuue kategooria jaoks ja viimane kategooria on faktori taustatase. Kui kuuendal faktori tasemel on dispersioonanalüüsi mudeli kohaselt (vt eespool: ühefaktorilise dispersioonanalüüsi põhimudel)  keskmiseks 6,81 (lisandub 0, vt veerg B), siis teisel tasemel on mudelipärane keskmine märgatavalt madalam: 6,81 − 0,94. Näeme, et selle taseme mõjukomponendi usaldusvahemik usaldusnivool 95% ei kata nullpunkti (−1,47 kuni −0,41), mis tähendab seda, et tasemele 2 vastava töömotivatsiooni korral (töökoha säilitamine) on eluga rahulolu keskmiselt madalam. (Loomulikult ei tea me, kumb kumma tingib, kas rahulolu motivatsiooni või vastupidi, vaid kõneleme praegu valitud mõtlemise skeemi kohaselt: eluga rahulolu võib oleneda sellest, mis ajenditel tööl pingutatakse.)

Iga mõjukomponendi μ_i puhul kontrollitakse hüpoteesi „üldkogumis  μ_i = 0“. Selleks kasutatakse ligikaudset reeglit, mille kohaselt mõjukomponendi ja selle standardhälbe (teine arvude veerg) suhe ehk t-statistik on selle hüpoteesi kehtides ligikaudu t-jaotusega. Igal tasemel (välja arvatud taustatase) osutatakse selle hüpoteesi olulisuse tõenäosus. Eluga rahulolu on kõigi vastuste puhul, välja arvatud vastus 2, statistiliselt keskmiselt mitteeristatav vastusest 6 iga praktikas mõeldava olulisuse nivoo korral. Vastuse 2 puhul on eluga rahulolu statistiliselt oluliselt madalam kui vastuse 6 puhul. Milline tase võtta taustatasemena võrdluse aluseks (mis tasemel komponent võtta nulliks), on uurija valida. Arutluse tausta valik võiks eeskätt toimuda sisu alusel, aga samal ajal ei tohiks see tasemegrupp olla liiga väike (tabelis 4 näeme ka tasemegruppide suurust).

Tabelis 4 näeme tasemegruppide keskmiste omavahelise paarikaupa võrdlemise kokkuvõtet (kasutatud on Scheffé testi ja Tukey testi), aga sama võib mitmest võrdlust silmas pidades teha ka Studenti testiga. Kaks võrdlustesti pakuvad pisut erisuguseid versioone keskmiselt ühetaoliste tasemete kohta. Scheffé testi alusel võib kolme esimesena nimetatud taset lugeda eluga rahulolu poolest keskmiselt ühetaolisteks olulisuse tõenäosusega 10% ja samal ajal viit viimast olulisuse tõenäosusega 15%. Paneme tähele, et  liigitus sisaldab kattuvusi (nagu tegelikus elus ongi). Tukey test pakub kolme alamrühma versiooni, kusjuures kaht esimest taset ja nelja viimast taset ei ole statistilist alust üksteisest keskmiselt eristada.

Dispersioonanalüüsi ideestikku sisseelamise sellega lõpetame ja soovitame lugejal tutvuda ka järgmiste käsitlustega:

http://www.uvm.edu/~dhowell/fundamentals7/SPSSManual/SPSSLongerManual/SPSSChapter8.pdf , David C. Howell,

http://davidmlane.com/hyperstat/, David Lane’i internetiõpik.

Reaalsed olukorrad nõuavad mitme mõjufaktori arvestamist korraga ja see muudab dispersioonanalüüsi väga kiiresti keeruliseks ülesandeks. Jutt ei ole üksnes matemaatilisest küljest, vaid tulemuste tõlgendamise raskustest. Sel põhjusel ei ületa kaasatavate faktorite arv praktikas tavaliselt kolme ja faktorite tasemete arv hoitakse samuti väiksena. Siinkohal piirdume kahefaktorilise analüüsi skeemiga, sest edasine üldistus kulgeb samamoodi. Põhimõtteliselt on üldistust kahe faktori juhule võimalik mõista üsna lihtsalt. Dispersiooni osade tähendus kahe faktori juhul on järgmine (vt võrdluseks ühefaktorilise mudeli skeemi (vt dispersiooni osad):

koguhälve =
esimese faktori poolt määratud tasemerühmade vahelistest erinevustest tingitud hälve +
teise faktori poolt määratud tasemerühmade vahelistest erinevustest tingitud hälve +
esimese ja teise faktori interaktsioonist (koosmõjust) tingitud rühmadevaheliste erinevuste osa koguhajuvuses + 
rühmadesisesest juhuslikust hajuvusest tingitud koguhajuvuse osa.

Lisandus teise faktori peamõju (ingl main effect, tumedam sinine) ja  kahe faktori koosmõjutegur ehk interaktsioonitegur (ingl interaction effect, hall). Interaktsioonitegurit ei pea lisama, aga vajadusel võib. Miks, selles püüame veenduda hiljem näite varal. Interaktsioonitegur väljendab seda osa faktorite mõjust, mis ilmneb seetõttu, et indiviid on ühekorraga positsioneeritud ühe ja teise faktori kindlale tasemele (nt on Eesti naine, mitte lihtsalt naine ja lihtsalt Eestist). Interaktsioonitegur väljendab, kuivõrd oleneb ühe faktori mõju sellest, milline on parajasti teise faktori väärtus.

Kahefaktoriline dispersioonanalüüsi mudel keskmise kohta avaldub täismudelina ehk kõiki komponente haarates järgmiselt:

kus m_ih on funktsioontunnuse keskmine esimese faktori taseme i ja teise faktori taseme h korral, a_i esimese faktori tasemele i vastav komponent, i = 1, 2, …, K (esimesel faktoril on K taset), b_h teise faktori tasemele h vastav komponent, h = 1, 2, …, M (teisel faktoril on M taset), t_ih faktorite tasemete kombinatsioonile i ja h vastav komponent  (kokku K×M tasemekombinatsiooni) ja m on kõigile tasemeile ühine konstant. Mudel ei pruugi olla täielik ja sageli jäetakse ära interaktsiooni komponent ning vaadeldakse peamõjude mudelit:

Formaalsed statistilised uurimisülesanded on järgmised. Uuritakse:

1. esimese faktori peamõju, selgitades, kui tõepäraselt on kõik esimese faktori tasemekomponendid a_i võrdsed nulliga (teiste sõnadega, puudub esimese faktori peamõju);
2. teise faktori peamõju, selgitades, kui tõepäraselt on kõik teise faktori tasemekomponendid b_h võrdsed nulliga (puudub teise faktori peamõju);
3. koosmõju, selgitades, kui tõepäraselt on kõik tasemekombinatsioonidele vastavad komponendid t_ih võrdsed nulliga (puudub esimese ja teise faktori interaktsioon).

Kahefaktorilise dispersioonanalüüsi ideed selgitab suurepäraselt simulatsioon aadressil  http://www.ruf.rice.edu/~lane/stat_sim/two-way. Jätkame kahe arvulise näitega.

Näitena vaatleme, kuidas varieerub Eestis ja Soomes keskmine hinnang noorte ja eakate panusele majandusellu olenevalt vastaja vanuseastmest, kasutades Euroopa sotsiaaluuringu 2008. aasta andmeid. Hinnangu andnute arv on Eesti puhul 1500 ja Soome puhul 2000 ringis. Vanusegrupp (kuni 35 aastat, 36–55, üle 55 kuni 75, üle 75)  ei ole faktorina väga selgelt eristuvate kategooriatega tunnus, sest naabergrupid on ühise piiriga, kuid siiski on need eluea sisuliselt selgelt eri osadel paiknevad grupid. Sõltuvaid tunnuseid on kaks (käsitleme eraldi näidetena): 20ndates aastates inimeste ja eakate panuse hinnang vastusena küsimusele „Kõike arvesse võttes, kas Teie meelest 20ndates aastates (vastavalt üle 70aastaste) inimeste panus riigi majandusse tänapäeval on suur või väike?“. Vastused anti skaalal 0 kuni 10, kus 0 tähendas väga väikest ja 10 väga suurt panust. Joonisel 2 on kujutatud nende tunnuste jaotused vanusegrupiti. Dispersioonanalüüsi rakendamisel on soodus (rangelt võttes: eeldatud) jaotuste lähedus normaaljaotusele, mis praegusel juhul praktikuna hinnates on päris suur (pidev joon histogrammil tähendab vastava ideaalse normaaljaotuse kõverat).

Alustame eakate panusest. Koostame dispersioonanalüüsi mudeli, võttes lisaks vanusegrupi tunnusele arvesse ka elukohamaa kui faktori mõju (julge oleks eeldada Eesti ja Soome täiesti sarnaseid hinnanguid) ja vaadeldes faktorite kõiki võimalikke mõjusid, sh ka kahe faktori interaktsiooni. Saadud dispersioonitabel on näha tabelis 5. Dispersioonitabeli tõlgendamine on täiesti analoogiline eespool käsitletud ühefaktorilise dispersioonanalüüsi dispersioonitabeliga (vt dispersiooni osad).

Vanusegrupi ja elukohamaa teadmine ehk mudel tervikuna võimaldab prognoosida eakate hinnangu varieeruvusest 16% (0,159 = 2974 : 18711). Dispersioonanalüüsi (dispersiooni osadeks lahutamise) tabelist näeme F-suhetele ja olulisuse tõenäosustele tuginedes, et kõik kolm hüpoteesi

hinnang Eestis on keskmiselt sama nagu Soomes (maa peamõju),

kõik vanusegrupid annavad keskmiselt ühe ja sama hinnangu (vanusegrupi peamõju),

vanusegruppide vahelised keskmised erinevused on Eestis samad mis Soomes ehk teisiti öeldes, kõigis vanusegruppides on Eesti ja Soome hinnangute erinevus keskmiselt ühesugune (maa ja vanusegrupi interaktsiooni mõju)

tuleb kummutada olulisuse tõenäosusega alla 0,05%. Jääkhajuvus ehk summaarne tasemetesisene ruuthälve on „väike“ võrreldes maadevahelistest erinevustest tingitud hajuvuse osaga ja vanusegruppidevahelistest erinevustest tingitud hajuvuse osaga, sh arvestades ka, et kumbki nimetatud osadest võib oleneda sellest, milline on parajasti teise faktori tase. Ruuthälvetele tuginedes võime öelda, et maadevahelised erisused on tulemuste hajuvuses kõige enam „süüdi“.

Et interaktsioonitegur ei ole kohustuslik, siis vaadelgem dispersioonitabelit ka ilma selleta (vt tabel 6). Mudeli kirjeldusaste on madalam kui interaktsioonide kaasamisel: 14% vs 16%. Niihästi vanusegrupp kui ka maa on hinnangu statistiliselt olulised faktorid väga väikese olulisuse tõenäosuse korral.

Kas võiks ka toimida nii, et jätta mudelisse ainult interaktsioonitegur, aga kõrvaldada peamõjud? Üldjuhul seda praktikas ei tehta. Oluline on mõista, et peamõjud interaktsioonidega mudelis ei mõõda vastava faktori kogumõju, sest faktor on kaasatud ka interaktsioonikomponenti. Peamõjudega mudelis tähendab peamõju kogumõju, aga iseküsimus on, kas peamõjudega mudel on alati adekvaatne (kui tegelikult toimib ka interaktsioon). Kui mudelis puuduvad peamõjud, aga on faktori interaktsioon mõne teise faktoriga, siis on interaktsiooniteguris hõlmatud nii peamõjud kui ka interaktsioonikomponent. Interaktsioonidega mudeli korral saame keskmiste täpse hinnangu (nagu on algandmeis), interaktsioonideta mudeli puhul ei pruugi saada.  Mida tähendab interaktsioon, seda selgitame oma näites mudelipäraste keskmiste prognooside graafiku varal (st keskmist hinnangut saadud mudeli alusel arvutades).

Maa ja vanusegrupi interaktsioon hinnangule avaldub selles, et eri vanusegruppides erinevad kahe maa prognostilised keskmised hinnangud teineteisest erineval moel: noorimas vanusegrupis vähe, järgnevates rohkem (vt joonis 3).  Teisiti kõneldes: Eestis on vanusegruppidevahelised erinevused prognostiliste keskmiste alusel teistsugused, nimelt väiksemad kui Soomes (sinised punktid on püstteljel üksteisele lähemal kui rohelised punktid). Keskmiste graafik on interaktsiooni tähtsuse hindamiseks visuaalselt väga ilmekas: kui keskmisi ühendavad jooned on enam-vähem paralleelsed, siis arvatavasti faktoritevaheline interaktsioon ei ole sõltuva tunnuse suhtes kuigi oluline. Kui jooned lõikuvad, siis tasub asja täpsemalt uurida. Meie näites on joonte üldmulje paralleelsusest kaugel.

Interaktsioonita ehk peamõjude mudelis on maadevahelised prognostilised erinevused kõigis vanusegruppides ühesugused (vt joonis 4). Teisiti võiks öelda, et interaktsioonideta mudeli korral paistavad vanusegruppidevahelised erinevused kahel maal ühesugustena. Joonte paralleelsus on meie eneste „tellitud“ peamõjude mudeli formuleerimisega.

Eestit-Soomet vanusegrupiti kokku võttes näeksime vanusegruppidevahelist keskmist erinevust (vanusegrupi mõju, laias laastus öeldes: mida kõrgem iga, seda soodsam hinnang). Vanusegruppe Eestis ja Soomes kokku võttes näeksime maadevahelist keskmist erinevust (elukohamaa mõju, hinnang Soomes kõrgem kui Eestis).

Prognostiliste keskmiste kujunemist mõjukomponentide kaudu saame jälgida mõjukomponentide (mudeli parameetrite) tabeli alusel. Vaatleme seda esmalt peamõjude mudeli korral. Tabelis 7 on esitatud suhtelisel skaalal kõigi nelja vanusegrupi jaoks keskmise komponent ja samuti mõjukomponendid kummagi maa jaoks. Esitus on suhteline selles tähenduses, et Soome tase loetakse nulltasemeks maa seisukohalt ja neljas vanuserühm vanusegrupi seisukohalt. Tabelis esitatud arvud näitavad erinevust kokkuleppelisest nulltasemest (vastavalt Soome hinnanguist ja vanima vanusegrupi hinnanguist). Näeme sama, mis jäi silma jooniselt 4: mida eakam on vastaja ise, seda kõrgema hinnangu ta annab eakate panusele (nt noorima vanusegrupi puhul on hinnang keskmiselt 1,3 võrra madalam kui vanimas grupis). Mõjukomponendi olulisuse tõenäosus aitab hinnata, kuivõrd tõepäraselt saab vanusegrupi keskmist lugeda sarnaseks taustaks võetud vanima vanusegrupi keskmisega (muidugi kui maa on üks ja sama; üldisemalt, kui ülejäänud tunnused on püsiva väärtusega). Näeme niisiis, et sarnasuse mõttest tuleb loobuda, millest on hinnangu sisule mõeldes tegelikult kahju. Ka usaldusvahemikud usaldusnivool 95% kinnitavad sama: ükski usaldusvahemik ei sisalda nullväärtust (nullerinevus on erinevuse puudumine taustagrupi suhtes). Olulisuse tõenäosus toetub t-statistikule – parameetri ja selle standardhälbe suhtele, mida kõrvutatakse teoreetilise t-jaotusega analoogiliselt ühefaktorilise juhuga. Soome hinnangud on keskmiselt 1,4 punkti võrra kõrgemad, kui vanusegrupp on üks ja sama. Nii näiteks on prognostiliselt teise vanusegrupi (36–55 aastat) keskmine hinnang vanemaealiste panusele Eestis järgmine: 5,60 − 0,71 − 1,44 = 3,45. Soome korral saame sama vanusegrupi korral keskmise prognoosiks:   5,60 − 0,71 = 4,89.

Tabelis 8 on esitatud dispersioonanalüüsi mudeli mõjukomponendid maa ja vanusegrupi interaktsiooni kaasates. Sellest tabelist näeme

peamõjusid: Eesti keskmine peamõjuna on 1,4 võrra madalam kui Soome keskmine (olulisuse tõenäosus alla 0,05%); alla 35aastaste antud hinnang on keskmiselt peamõjuna 1,7 punkti võrra madalam kui üle 75 aasta vanuste antud keskmine hinnang (olulisuse tõenäosus alla 0,05%),

interaktsiooni: Eesti ja Soome keskmiste hinnangute erinevus kuni 35aastaste seas on 0,9 võrra väiksem kui vanemate kui 75aastaste seas (olulisuse tõenäosus alla 0,05%); vanuses 56–75 ja vanemate kui 75aastaste antud hinnangute erinevus on Eestis keskmiselt 0,7 võrra suurem kui Soomes; vanuses 36–55 ja vanemate kui 75aastaste antud hinnangute erinevus on Eestis ja Soomes sama (olulisuse tõenäosus 0,38, usaldusvahemik katab nullpunkti).

Kokku on mudeliga grupiti määratud kaheksa avaldist vanemaealiste panuse hindamiseks keskmiselt. Keskmise esitus mõjukomponentide kaudu on järgmise skeemi kohane.

Eesti, kuni 35-aastased:
5,60 (vabaliige) − 1,44 (maa peamõju Eesti jaoks) − 1,69 (vanusegrupi peamõju kuni 35aastaste jaoks) + 0,93 (vanusegrupi ja maa interaktsioon Eesti ja kuni 35aastaste jaoks) = 5,60 −1,44 −1,69 + 0,93.                
Soome, kuni 35aastased:    5,60 − 1,69.
Eesti, 36–55 aastat vanad:     5,60 − 1,44 − 0,61 − 0,24.
Soome, 36–55 aastat vanad:    5,60 − 0,61.
Eesti, 56–75 aastat vanad:     5,60 − 1,44 − 0,05 − 0,71.
Soome, 56–75 aastat vanad:  5,60 − 0,05.
Eesti, vanemad kui 75 aastat: 5,60 − 1,44.                        
Soome, vanemad kui 75 aastat: 5,60.

Vanusegrupi 4 (taustagrupp) ja vanusegrupi 1 erinevus Eestis (lahutame ühe mudeli kirjutise teisest) on keskmiselt 1,69 − 0,93 = 0,76. Sama erinevus Soome andmeil on 1,69 (seega suurem, vt ka joonis 3). Paneme tähele, et Eesti ja Soome „erinevuste erinevus“ nende vanusgruppide vahel on võrdne keskmiselt interaktsioonikomponendiga. Lugeja võib seda mõtet kontrollida ka teiste vanusegruppide korral. „Erinevuste erinevus“ ongi interaktsioonikomponendi tähenduse otsimisel väga kasulik sõnapaar, juhul kui mudelis on ka peamõjud.

Teiselt poolt võiks vaadelda ka Soome ja Eesti mudelipärast erinevust erinevates vanuserühmades. Nii näeme, et vanimas vanusegrupis on see 1,44, aga noorimas vanusegrupis 1,44 – 0,93 (st vähem, vt ka joonis 3), seejuures täpselt interaktsioonikomponendi võrra. Vanusegrupi 2 korral, mil interaktsioonikomponent on statistiliselt mitteoluline iga mõeldava olulisuse nivoo puhul, on „erinevuste erinevus“ väike — üksnes 0,24.

Vaatleme dispersioonanalüüsi mudeli varal ka kahekümneaastaste põlvkonna hinnanguid. Tabelis 9on kõigepealt esitatud hinnangute keskmised vanusegrupiti kahel maal. Näeme jälle, et aritmeetiliselt on Soome vastajate hinnangud keskmiselt kõrgemad, samuti märkame kahel maal varieeruvust vanusegrupiti. Kas see on ka statistiliselt oluline mõnel mõistlikul olulisuse nivool, sellele otsimegi vastust dispersioonanalüüsi mudelit koostades.

Standardhälbed on Eesti puhul suuremad (1,9 ringis) kui Soome puhul (1,7 ringis). Dispersiooni sama tase grupilt grupile liikudes on üks dispersioonanalüüsi eeldusi ja selle täidetust aitab analüüsida joonisel 5 esitatud tasemegruppide dispersioonide graafik tasemekeskmiste suhtes. Suurima ja vähima dispersiooni suhe on alla 1,5, kusjuures selget ohtu dispersiooni püsivuse eeldusele nähakse kogemuslikult, kui see suhe on üle 2-2,5-3. Hea seis analüüsiga edasiminekuks on siis, kui seda tüüpi jooniselt ei paista mingit seaduspära, st dispersioon ei olene keskmise suurusest, kui vaadelda kõiki tasemegruppe (pange tähele püsttelje väikest ulatust: 2,75 kuni 3,75).

Tabelis 10 on esitatud noorte panuse hinnangute dispersioonitabel, mis on ülesehituse poolest analoogiline eakate panuse mudeliga (vt ka tabel 6). Näeme, et mudeli kirjeldusaste tuleb väiksem: eakate panuse mudelis 16%, siin alla 11%. Niihästi vanusegrupi kui ka maa peamõju ja nende interaktsioon osutuvad statistiliselt oluliseks väga väikese olulisuse nivoo korral (alla 0,05%). Ka selles mudelis on elukohamaa tugevaim mõjutegur. Interaktsioonitegur on nõrga kirjeldusvõimega (vrd summaarseid ruuthälbeid).

Tabelis 11 on esitatud noorte panuse mõjukomponentide loetelu ja selle alusel võib lugeja nüüd võrdlevalt analüüsida, milles seisneb erinevus Eesti ja Soome hinnangute vahel, milline on vanusegrupi diferentseeruv mõju ja milles seisnevad „erinevuste erinevused“. Kasu oleks, kui skitseerida ka keskmiste graafik analoogiliselt joonisele 3. Eesti puhul näeme, et keskmised hinnangud on vanuse suurenedes langevas suunas, kuid erinevused keskmistes vastaja vanuse kasvades vähenevad (liidame vanusegrupi peamõju ja interaktsiooniteguri):  vanusegrupiti vastavalt

0,26 + 0,98 = 1,24,
−0,36 + 0,72 = 0,36,
−0,29 + 0,48 = 0,19,
0.

Soome puhul hinnang vanusegrupilt vanusegrupile suurema vanuse suunas liikudes küll langeb, aga ka mitte ühtmoodi: esmalt suurem väärtus võrreldes vanima grupiga, seejärel väiksem, aga ühtlustuv hinnang.

Näeme, et kolme esimese vanusegrupi puhul on erinevus vanima grupi hinnanguist Eesti puhul keskmiselt suurem kui Soome puhul (interaktsioonitegur on statistiliselt usaldusväärne olulisuse nivool 5% ringis). Näiteks saame järgmised  prognostilised väärtused:

Eesti, vanusegrupp 1 –  5,73 − 1,68 + 0,26 + 0,985,
Soome, vanusegrupp 1 – 5,73 + 0,26,
Eesti, vanusegrupp 4 – 5,73 – 1,68,
Soome, vanusegrupp 4 – 5,73,
vahe – 0,985 ehk interaktsioonikomponendi väärtus.

Loetleme mõned praktiliste rakenduste jaoks olulised asjaolud.

Esmalt tuleks kindlasti vaadelda faktori eri tasemetel sõltuva tunnuse keskmisi soovitatavalt koos usaldusvahemikega ja standardhälbeid – tuua juba sissejuhatavalt esile põhjalik kirjeldav statistika. Hoolikalt tuleb kaaluda, kas faktor peab teoreetiliselt vett, st ei ole tegemist andmetes formaalselt esiletulnud erisustega.

Faktorite hindamine ja valik toimub eeskätt uurimisküsimusest lähtuvalt, aga samuti dispersioonanalüüsi eeldustest lähtuvalt. Sisust tuleneb ka see, kas andmetele sobitatakse täismudelit või mõnd muud mõjude-koosmõjude mustrit väljendavat mudelit. Kui mudel ei ole täielik (mõni komponent on välja jäetud), siis ei tule keskmiste prognoos aritmeetiliselt täpne. Kui väljajäetud komponendid ei ole statistiliselt olulised, siis oleme sellegipoolest saanud kõlbliku mudeli, mis on  tõlgenduse poolest lihtsam, kui on täielik mudel. Peaks püüdlema võimalikult ökonoomse mudeli poole keskmise jaoks, mis tähendab statistiliselt mitteoluliste mõjukomponentide kõrvalejätmist mudeli ülesehitamisel.

Oluline on jälgida dispersioonanalüüsi eeldusi ehk kitsendusi andmetele. Tänapäeval on dispersioonanalüüs arvutiprogrammina realiseeritud üldise lineaarse regressioonimudeli vormis ja seetõttu on nõutavad üldised lineaarse mudeli kohta püstitatud eeldused (vt viide [Regressioonanalüüs]).

Funktsioontunnus (sõltuv tunnus) peab olema mõõdetud arvulisel skaalal.

Faktoreid käsitletakse kategoriaalsete tunnustena. Faktorid peavad väljendama selgelt eristuvaid omadusi selgelt eristuvate tasemerühmade kaudu.

Faktorid ei tohiks olla omavahelises sõltuvuses (see tingimus ei välista interaktsiooni sõltuva tunnuse suhtes).

Faktori mõju sõltuvale tunnusele peab olema ühetaoline: faktori eri tasemetel peab sõltuva tunnuse (mudeli vea) dispersioon olema ühesugune, dispersioon ei tohi muutuda sõltuva tunnuse tasemekeskmisest olenevalt.

Faktorite mõju usaldusväärsuse analüüsil on oluline sõltuva tunnuse (mudeli vea) jaotuse lähedus normaaljaotusele.

Tasemerühmade võrdne suurus on hea olukord ja teatud lihtsamate algoritmide korral lausa eeldatakse seda.

Kuidas hinnata tulemuse sisulist tähtsust? Mõju statistilist usaldusväärsust väljendava tõenäosusliku otsustuse kõrval on tähtis uurida, kui suured on arvuliselt vastavad tasemekomponendid, kasutades kindlasti ka nende usaldusvahemikke. Hüpotees iga mõjukomponendi kohta on „mõjukomponent võrdub nulliga“. Usaldusvahemiku puhul tuleb jälgida nullpunkti katmist usaldusvahemikuga, millele vastabki selle hüpoteesi paikapidamine.

Olulised on summaarsete ruuthälvete protsentuaalsed osakaalud koguhälbest (R²), et mõista ühe või teise mõjukomponendi tähtsust mudelis. Kui võimalik, võiks mõjukomponente kaalukuse poolest mudelis kõrvutada (summaarsete ruuthälvete alusel, F-suhete alusel. NB! F-suhete võrreldavus kehtib üksnes ühtede ja samade vabadusastmete arvude korral).

Tulemuste esitlus oleneb auditooriumist, kellele töö läheb.

Laia kuulajaskonna ees on eeskätt oluline esile tuua sõnum, mis tegurid sõltuvat tunnust diferentseerivad ja mil viisil (mis suunas on mõju). Suurepärane on esitada keskmiste graafik ja osutada need erisused, mis on statistiliselt usaldusväärsed nt olulisuse nivool 5% ja (NB!) seejuures tähenduse poolest märkimisväärsed.

Kui tulemused on suunatud dispersioonanalüüsi idee poolest tundvale lugejale-kuulajale, siis võib esitada keskmiste graafiku koos erinevuste statistilise olulisuse näitamisega, aga ka dispersioonitabeli ja teha juttu mudeli kirjeldusvõimest. 

Professionaalsem auditoorium tunneks huvi ka mõjukomponentide tabeli ehk mudeli vastu ja tahaks kuulda, kuivõrd hästi olid täidetud dispersioonanalüüsi eeldused, vähemalt mõned neist. Loomulikult on ka siin mudelipäraste keskmiste graafik väga teretulnud. 

Oluline on tulemuste täpsusaste. Eeltoodud tabeleis on sellega vahel liiale mindud ja kasutatud liigset täpsust. Mõelda tuleb lihtsalt: kui saime arvandmed teatud  täpsusega, siis tulemustes ei ole vaja lisada rohkem kui üks kümnendkoht (täisarvudele üks komakoht jne). Summaarsed ruuthälbed võiksid kõik olla täisarvud. F- ja t-suhtel võiks osutada kaks tüvenumbrit, samuti olulisuse tõenäosusel (nt 0,035; 0,35; 0,00035).

Joonised ja graafikud on nii keerulise mudeli korral, nagu on seda mitmefaktoriline dispersioonanalüüs, väga olulisel valgustaval kohal.

http://www.uvm.edu/~dhowell/fundamentals7/SPSSManual/SPSSLongerManual/SPSSChapter8.pdf , David C. Howell.

http://davidmlane.com/hyperstat/, David Lane’i internetiõpik.

http://www.ats.ucla.edu/stat/spss/topics/anova.htm Paketi SPSS kasutamine dispersioonanalüüsi jaoks.

Tooding, L.-M. (2007). Andmete analüüs ja tõlgendamine sotsiaalteadustes. Tartu, Tartu Ülikooli Kirjastus. Ptk 6.4.